IE1.Signals&Amplifiers
IE1.Signals&Amplifiers #
Last Edit: 9/4/25
1.1 Signals #
- 信号包含了关于物理世界中各种活动和事物的信息
- 很多的东西都可以归于信号,例如 Temperature, Pressure, Wind Speed 等
Processing Signals #
- 为了从 Signals 中提取有效的信息,则需要进行 Signal Processing
- 但是在这之前,人需要将其转换为 Voltage 或者 Current
Signal Source #
- 信号源同 Source 一样,显示世界中并没有 Ideal Source,即 Zero Resistance
- 所以这就需要给 Source 添加一个 Resistor,其可以通过Thevenin Form 来表达
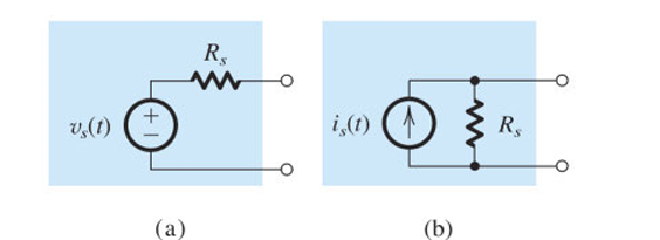
- 上图两种表示方法是等效的
1.2 Frequency Spectrum of Signals #
- 研究信号时,一个非常重要的方式是用它的 frequency spectrum 来表示
- 通过 ****Fourier series(傅里叶级数)和 Fourier transform(傅里叶变换),能把任意信号表示成不同频率和幅度的 sine waves之和
- 所以,sinusoid 是电子学里最重要的信号形式之一

- 上图是一个 Sine-wave Voltage Signal,其表达式为
$$ v_a(t) = V_a \sin(\omega t) $$
其中:
- \(V_a\):amplitude 振幅 ,单位 V
- \(\omega\):angular frequency 角频率,单位 rad/s
- f:frequency 频率,单位 Hz,关系为 \(\omega = 2 \pi f\)
- T:period 周期,单位 s,关系为 \(f = 1/T\)
RMS Root Mean Value #
- Sine Wave 常用 Root-Mean-Square 来表示,这是因为 Sine Wave 图像的对称性(奇函数)导致的其在取传统 Mean 的时候正负会相互抵消,而又需要一个能反映它产生的 Energy 或者 Power 的值,于是就有了 RMS
$$ V_{rms} = \frac{V_a}{\sqrt{2}} $$
举例:
- 家庭电源(wall power supply)标称 120 V,实际上是正弦波的 rms 值,
- 所以峰值电压是 \(120\sqrt{2} \approx 170 V\)
Fourier Series #
- 然而,就像前面的 Thevenin 一样, 真实情况下的 Signal 一般并不全是 Sine Wave,这导致他们无法被用一个简单的公式直接分析

- 所以 Fourier Series 的思想就是将任意的 Complex Signals 分解成一堆 Sine Waves 的组合
Sine Wave 就可以类比为 Signal 中的 Atoms, they made up everything
- 对于上面的 Square-Wave 来说,它的傅里叶展开结果为
$$ v(t) = \frac{4V}{\pi}\left(\sin \omega_0 t + \frac{1}{3}\sin 3\omega_0 t + \frac{1}{5}\sin 5\omega_0 t + \cdots \right) $$
- V:方波幅度
- \(\omega_0 = \frac{2\pi}{T}\):Fundamental Frequency 基频角频率
- 这个公式说明:
- Square Wave 其实是由无穷多个正弦波叠加而成
- 其只包含odd harmonics 奇次谐波:\(\omega_0, 3\omega_0, 5\omega_0…\)
- 每个谐波的 Amplitude 随着频率升高而减小(与 1/n 成正比)
Line Spectrum #
- 一个 Wave 包含了一个基波加上无数个谐波,而对于这个 Square Wave 来说,想要画出它的 Frequency 的成分,就可以通过 Line Spectrum
- 其中每一根竖线代表信号在该频率下的一个正弦波分量

- 基频分量(\(\omega_0\))的幅度是 \(\frac{4V}{\pi}\)
- 第三次谐波(\(3\omega_0\))幅度是 \(\frac{1}{3}\frac{4V}{\pi}\)
- 第五次谐波(\(5\omega_0\))幅度是\(\frac{1}{5}\frac{4V}{\pi}\), 依此类推
- 方波看起来是“方形”的,但它实际上是这些频率分量正弦波叠加的结果。
Representations #
- 总的来说,表达 Signals 有两种方式,Time-Domain 和 Frequency-Domain
- 时域看信号随时间的波形,频域看信号的频率成分
1.3 Analog and Digital Signals #
Analog Signal #
- Analog Signal 模拟信号,指的是这个信号是 Analogous 模拟他所表示的实际信号的
- 其中其 Amplitude 可以取任意值,其在图像中是 Continuous Variation 连续变化的
Digital Signal 数字信号 #
- 通过一系列数字来表示某个时间点的 Signal Amplitude 的叫做 Digital Signal 数字信号
- 他就是从 Analog Signal 中 Sampling 得到的

- Digital Signal 仅仅在 Sampling 的时候有定义,其不再是一个 Continue Function,而是 Discrete-Time Signal
Type of digital signal #
- 不同的 Number System 下,Digital Signal 的表示形式也将不一样
- 其中 Binary Number System 是最常见的,其只有 0 和 1,也就是高电平和低电平

- 这张图中,蓝色波形表示一个 binary digital signal 随时间的变化
- 如果用 N binary digits, 表示模拟信号的每个采样值,那么数字化后的采样值可以写成:
$$ D = b_0 2^0 + b_1 2^1 + b_2 2^2 + \dots + b_{N-1} 2^{N-1} $$
其中:
- \(b_0, b_1, …, b_{N-1}\) 是 比特(bits),取值只能是 0 或 1
- \(b_0\) 是 LSB least significant bit,最低有效位
- \(b_{N-1}\) 是 MSB most significant bit,最高有效位
- 这个二进制数通常写作 \(b_{N-1} b_{N-2} … b_0\)
- 结果是:一个模拟采样值被量化(quantized)到 \(2^N\) 个可能的等级(levels)中
之所以是 \(2^N\) 是因为整个 Signal 被当做了一个 Binary Number
- N 越大,数字结果就越接近真实模拟值,量化误差(quantization error)就越小,但电路更复杂、成本更高
A/D converter #
- A/D converter 模数转换器,Analog-to-Digital Converter, ADC
- 顾名思义将 Analog Input 转换为 Digital Output
- 而中间的模块首先 Sampling,在 Decent 的时间点上读取 Signal
- 之后将连续的 Voltage 逼近到 \(2^N\) 个能级中,举例来说有
- 假设输入电压范围是 0 V ~ 5 V
- 在这个范围里,电压可能是 2.53 V、3.1415 V、甚至 4.00001 V,理论上是无限多的可能值
- 这很合理,因为 Analog Signal 是 continuous 的,而 ADC 不能处理无限多的值,它必须用有限的比特数(二进制位)来表示
- 假设是 3-bit ADC(N=3):
- 它最多能表示 \(2^3 = 8\) 个等级(levels)
- 那么 0~5 V 的输入范围被均匀分成 8 段,每一段宽度是:\(\frac{5}{8} = 0.625 , \text{V}\)
- 于是:
- 输入 0~0.625 V → 输出 000
- 输入 0.625~1.25 V → 输出 001
- 输入 1.25~1.875 V → 输出 010
- 输入 1.875~2.5 V → 输出 011
- 输入 2.5~3.125 V → 输出 100
- 输入 3.125~3.75 V → 输出 101
- 输入 3.75~4.375 V → 输出 110
- 输入 4.375~5.0 V → 输出 111
- 将所有的 Binary Number 组合后将其表示出来最终 Encoding 得到结果
- 然后就是输出成 Analog Output
1.4 Amplifiers #
- Signal Processing 中,一个最基本的功能就是 Signal Amplification 信号放大
- 这就需要研究 Amplifier 的作用
1.4.1 Signal Amplification #
- Signal Amplifier 信号放大器的功能就是把微弱的信号,如 \(\mu V,nV\) 级别的信号放大到足够大,便于后续的处理
- 而其关键的需求就是 Linearity 线性
- 即在 Signal 被放大后,Wave 因保持不变,只是 Amplitude 更大
- 其中如果 Wave 的形状发生了改变,即 Distortion 失真
- Amplifier 的功能用公式表达出来就是
$$ v_o(t) = A v_i(t) $$
- \(v_i\):input signal(输入信号)
- \(v_o\):output signal(输出信号)
- \(A\):amplifier gain(放大器增益),是常数
Voltage Amplifier (电压放大器) #
- 主要处理很小的输入电压信
- 目的:让信号幅度更大
- 示例:preamplifier(前置放大器),在家庭音响系统(home stereo system)中常见
Power Amplifier (功率放大器) #
- 功能:提供足够的功率给负载(例如 loudspeaker 扬声器)
- 特点:电压增益可能不大,但功率输出很大
- 扬声器是系统的 output transducer(输出换能器),将电信号转换为声音信号
- linear power amplifier(线性功率放大器) 能保证无论大音量还是小音量,音乐都不会失真
1.4.2 Amplifier Circuit Symbol #

- 一个完整的 Amplifier 应如上图,存在一个 Input 和 Output,同时有 Ground
1.4.3 Voltage Gain #

- 负载电阻:\(R_L\) (load resistance 负载电阻)
- 放大器把输入信号放大,输出端得到放大的复制品。
- 电压增益 (Voltage gain 电压增益) 定义为:
$$ A_v = \frac{v_o}{v_i} $$
- 左边:输入电压 \(v_i(t)\)
- 三角形:电压放大器 (voltage amplifier 电压放大器)
- 右边:负载电阻 \(R_L\),输出电压 \(v_o(t)\) 在其两端产生
- 其中整个 Transfer 过程都将是 Linear 的(理想状态下)
1.4.4 Power Gain and Current Gain #
- 已知 Power = Current \(\times\) Voltage
- 所以对于 Power 的增益定义为
$$ A_p = \frac{P_L}{P_I}= \frac{v_O i_O}{v_I i_I} = A_v \times A_i $$
1.4.5 Expressing Gain in Decibels #
- Decibels 分贝,是一个对数数据,在工程中使用如此对数数据的好处是在多个 Amplifier 相乘的时候,Log 的运算便为 Addition
- 同时 Current,Voltage 和 Power 本质上是无纲量,于是有
$$ \text{Voltage gain (dB)} = 20 \log |A_v| $$
$$ \text{Current gain (dB)} = 20 \log |A_i| $$
$$ \text{Power gain (dB)} = 10 \log A_p $$
- 这里的系数值得说明一下,首先对于 Decibels 的定义是从 Power 开始的,有
$$ G_{dB} = 10 \log_{10} \left( \frac{P_{out}}{P_{in}} \right) $$
- 这个 “10” 是最原始的定义,和功率的物理意义绑定。
- 在相同电阻 R 下:\(P = \frac{V^2}{R}\),于是有
$$ \frac{P_{out}}{P_{in}} = \left(\frac{V_{out}}{V_{in}}\right)^2 $$
$$ G_{dB} = 10 \log \left(\frac{P_{out}}{P_{in}}\right) = 10 \log \left(\frac{V_{out}}{V_{in}}\right)^2 = 20 \log \left(\frac{V_{out}}{V_{in}}\right) $$
- 所以电压增益、电流增益的 dB 表达式是 20 log,完全是从功率的 10 log 定义 推出来的。
- 拿 Power Gain 举例来说,当 \(A_p\) 为 10 的时候,Power Gain 为 0 dB
- \(A_p\) 为 100 的时候,Power Gain 为 40 dB,\(A_p\) 为 1000 的时候,Power Gain 为 60 dB
- 这就说明了 dB 的增加实际上是底数的倍数级上升
1.4.6 The Amplifier Power Supplies #
- 已知 Amplifier 送到 Load 的功率比从 Signal Source 获得的功率大,而那一部分多余出来的功率就是从 DC Power Supplies 直流电源 中获取

- 其中正电源为 \(V_{CC}\),负电源为 \(V_{EE}\)
- 对于 Amplifier 来说,其存在两个端子,一个接 \(V_{CC}\),一个接 \(V_{EE}\) 剩下的接地
DC power 直流功率 #
- 于是就可以得出 DC Power 的 DC 功率为
$$ P_{dc} = V_{CC} I_{CC} + V_{EE} I_{EE} $$
-
有 Power-balance equation 功率平衡方程
$$ P_{dc} + P_I = P_L + P_{dissipated} $$
- \(P_I\):信号源供给的功率(power from signal source)
- \(P_L\):负载功率(power delivered to load)
- \(P_{dissipated}\):放大器内部消耗(功率转为热 dissipated power)
Amplifier efficiency 放大器效率 #
- 因为 \(P_I\) 很小,可以忽略,所以效率定义为:
$$ \eta = \frac{P_L}{P_{dc}} \times 100 $$
1.4.7 Amplifier Saturation #

- Amplifier 在一定范围中是 Linear 的
- 但是一旦输出过大或者过小,Output 的 Voltage 就会到达电源的极限,导致其无法再继续增加或减小,Saturation 就出现了
- 图中用 \(L_+\) 表示 Positive saturation level 正饱和电平
- 用 \(L_-\) 表示 Negative saturation level 负饱和电平
- 通常 \(L_+\) 和 \(L_-\) 会比 Power Supply 电源电压)低一点点(几分之一伏),因为电路元件本身有压降
To Avoid Distortion #
- Distortion 是一个非常宽泛的实践,其会发生在很多种不同的情况下,其中 Clipping 就是其中一种

- 如图中,直线在途中说明的就是 Amplifier 的数学规律,即 Input 和 Output 的关系
- 其在输入到达一定大小的时候会不再变化
- 而 Wave 则是 Signal 随 Time 的变化情况,说明了真实信号在时间上运行的时候的行为,即 Clipping
- 而为了避免波形被 Clipping 削波,输入电压必须限制在一定范围内:
$$ \frac{L_-}{A_v} \le v_I \le \frac{L_+}{A_v} $$
- 这里 \(A_v\) 是放大器 voltage gain 电压增益
- 意思是:输入信号幅度必须在这个范围,输出才不会超出线性区
1.4.8 Symbol Convention #

-
电流 \(i_C(t)\) = total instantaneous current 总瞬时电流
-
它由两部分组成:
- DC component 直流分量): \(I_C\),是一个恒定值
- Signal component 信号分量): \(i_c(t)\),随时间变化,一般是正弦波
-
数学式:
$$ i_C(t) = I_C + i_c(t) $$
-
如果 \(i_c(t)\) 是正弦波则有
$$ i_c(t) = I_c \sin \omega t $$
1.5 Circuit Models for Amplifiers #
- 在电路设计里,amplifier 的内部结构可能很复杂,比如有的只用一个 transistor 晶体管,有的要几十个器件
- 但是我们在系统中使用放大器时,不需要关心它的内部细节,只需要关心它的 Terminal Behavior,也就是输入端和输出端是怎样的
1.5.1 Voltage Amplifiers #
- 一个 Voltage Amplifiers 如下图

Voltage-Controlled Voltage Source #
- 首先定义一个 Voltage-Controlled Voltage Source 电压控制电压源的 Gain Factor 增益因子为 \(A_{vo}\)
- 这是一个理想化的模型,意思是输出电压完全由输入电压决定
- 在这里,它的关系是
$$ v_{out} = A_{vo} \cdot v_{in} $$
- 其中 \(A_{vo}\) 就是增益系数(gain factor 增益系数)
- 可以理解为:这个“源”相当于一个“自动倍增器”,把输入电压放大 \(A_{vo}\) 倍
Voltage Source #
- 在介绍任何的 Circuit Element 之前,先来介绍一下 Voltage Source
- 一个 Source 并不是 Ideal 的,即其自身也存在一个 内部的 Resistor

- 于是这里就出现了第一个 Resistor \(R_S\)
Input Resistance #
- 当 Signal Source 把 Voltage 送入 Amplifier 时,放大器输入会端口“呈现出来”一个 Resistor
- 而将这个等效的 Resistor 称为 Input Resistance,其大小即为 \(R_i\)
- 到目前为止,已经理通了从 Voltage Source 到 Amplifier 的完整线路,实际的 Input Circuit 如下
$$ v_s⟶R_s⟶R_i⟶Amplifier $$
- 由于整个 Circuit 是一个 Series 的链接,所以 Amplifier 得到的 Voltage 将会被分压,即 \(R_s\) 和 \(R_i\) 构成了一个 Voltage Divider 分压器
- 其实际得到的 Voltage 为
$$ v_i=v_s⋅\frac{R_i}{R_s+R_i} $$
- 现在来分析一下 \(R_i\) 和 \(R_s\) 的数值对整体 Amplifier 的影响
- 当 \(R_i \gg R_s\)(输入电阻非常大)
$$ v_i \approx v_s \cdot \frac{R_i}{R_i} = v_s $$
- 输入电压几乎等于信号源电压,几乎没有损失
- 信号源几乎不用提供电流(因为电流 \(I = v_s / (R_s + R_i)\),而分母很大)
- 这是理想情况
- 当 \(R_i \ll R_s\)(输入电阻很小)
$$ v_i \approx v_s \cdot \frac{R_i}{R_s} \ll v_s $$
- 输入电压会被大大削弱。
- 电流 \(I \approx v_s / R_s\),信号源要提供很大的电流
- 结果:放大器“吃掉”了信号源的电压,损失严重
- 所以,好的电压放大器希望 Input Resistance 尽可能大
Output Resistance #
- Amplifier 本身并不是一个 Ideal 的 Dependent Voltage Source,他也有内部的 Resistance,就是 \(R_o\)
- 当 Amplifier 的 Output 想要驱动最终的 Load 的时候,它和 \(R_L\) 形成分压
$$ v_o = A_{vo} v_i \cdot \frac{R_L}{R_L + R_o} $$
- 同理,如果 \(R_o\) 较大,输出电压就会被“吃掉”一部分
- 如果 \(R_o\) 越小,输出电压就越接近理想值 \(A_{vo} v_i\)
- 所以,好的电压放大器希望 输出电阻尽可能小

- 再加上 Source 和 Load,整个 Circuit 就完成了
- 接下来将两个 Voltage Divider 乘在一起就得到了完整的 Overall Voltage Gain
$$ \frac{v_o}{v_s} = A_{vo} \cdot \frac{R_i}{R_i + R_s} \cdot \frac{R_L}{R_L + R_o} $$
1.5.2 Cascaded Amplifiers #
- 可以同时添加多个 Amplifiers ,计算他们的区别就是多了几个 Voltage Divider

