IMP 1. Review of Vector
IMP1.ReviewofVector #
Last Edit: 9/7/25
Scalar & Pseudoscalars #
Scalar 标量 #
- Scalar 只有 magnitude 没有 direction数学上定义:
一个 Scalar 是在任意坐标变换(包括旋转、反射、平移)下保持不变的数量
- 不论你怎么看它(换坐标系、换角度、翻转世界),它的数值都不变
- 所以它是“绝对的数值”
常见例子: #
| 标量(Scalar) | 单位 | 意义说明 |
|---|---|---|
| 质量(mass) | kg | 不管从哪个方向看,质量就是那么多 |
| 温度(temperature) | °C, K | 没有方向性,就是个数值 |
| 时间(time) | s | 没有方向,只是过去多少秒 |
| 电压(voltage) | V | 某点电势差(可以是正负,但不是方向) |
| 能量(energy) | J | 总能量多少,不依赖空间方向 |
Scalar field 标量场 #
- Scalar field 是一个 function,它接收一组 Scalar inputs,例如空间中的位置,并输出一个scalar output
- 比如说房间里的温度分布就是一个标量场
- 如果我们在二维空间输入位置 \((x,y)\),比如 \((1,1)\),函数 \(T(x,y)\) 会返回该点的温度
Pseudoscalars 伪标量 #
- Pseudoscalars 是看起来像标量(只有大小、没有方向)
- 但在parity inversion (空间反射)下会变号的量
Position Vectors & Vector Fields #
Pseudovector 伪向量 #
- Pseudovector 由两个普通 Vector Cross Product 产生
- 它的特性是当 Parity Inversion 时,方向不发生变化,即还是之间的两个 Vector 的 Cross Product 的位置
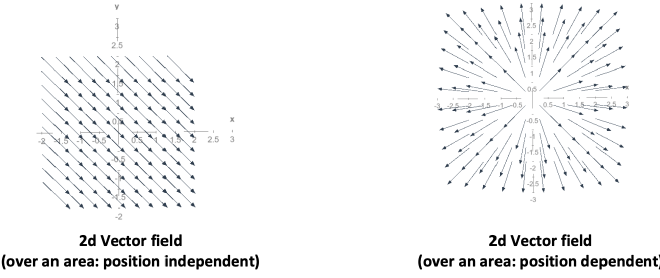
Vector field 向量场 #
- 向量场是一个函数,它在空间中的每一个位置上返回一个向量
- 三维空间中的 electric field 典型的向量场
- 由于一个 point charge Q 在空间产生的电场 \(\mathbf{E}\),就是一个向量场
- 标量场 → 每个点只给一个数值
- 向量场 → 每个点给一个向量,既有大小又有方向
Orthonormal Basis Vectors & Dot Product #
Orthonormal Basis Vectors 正交归一向量 #
- 在一个空间中,Orthonormal Basis Vectors 具有的特性就是 Orthogonal:互相垂直,Normalised:长度为 1
Dot Product 点积 #
- 计算一个 Vector 在另一个 Vector 方向上的 Projection
Cross Product 叉积 #
- 正如前面所提到的,两个 Vectors Cross Product 的结果将会是一个 Pseudovector 伪向量
Planes & Lines #
Line in Space #
- 在 \(\mathbb R^3\) 中,Two Distinct Point,或者一个 Point 加一个 Direction Vector 都可以可以确定一个 Unique Line
- 想要描述这一条 Unique Line 也可以通过 Parametric 和 Vector Equations
Plane Equation #
- Plane 的 Equation 为 \(ax + by + cz = d\)
Curved Surface #
- 曲面上的法向量不是固定的,而是与位置 \((x,y)\) 有关
- \(\vec{n} = \langle x, y, 1 \rangle \quad \text{或} \quad \langle -x, -y, -1 \rangle\)
Equation of a Plane Given Three Points #
- 已知三个点后,就可以得到一个同时穿过这三个点的 Plane Equation
e.x. #
- 假设 \(\mathbb R^3\) 中有三个点 O = (2, -1, 3),Q = (1, 4, 0),R = (0, -1, 5)
- 要求平面方程 \(ax + by + cz = d\)
- 需要知道法向量 \(\vec{n} = \langle a,b,c\rangle\),有了这个 Normal Vector 就可以得到 Plane 的 Equation
- 首先在 Plane 上找到两个 Vector \(\vec{OQ} = Q - O = \langle -1,5,-3\rangle\) 和 \(\vec{OR} = R - O = \langle -2,0,2\rangle\)
- 通过将这两个 Vector 做 Cross Product 就可以得到
$$ \vec{n} = \vec{OQ} \times \vec{OR}= \begin{vmatrix} \hat{x} & \hat{y} & \hat{z} \ -1 & 5 & -3 \ -2 & 0 & 2 \end{vmatrix} = \langle 10,8,10\rangle $$
- 就可以得到 \(10x+8y+10z = d\),带入任意一点就可以求出 d
Equation of a Plane Given That 2 Lines Intersect #
- 两条相交的 Line 也可以在 \(\mathbb R^3\) 中围出一个唯一的 Plane
- 假设有两条 Line
$$ Line ~1: x = t,\ y = 2t + 1,\ z = 3t + 4 $$
$$ Line~2:x = 2s - 2,\ y = 2s - 1,\ z = 3s + 1 $$
- 他们的 Intersection 即出现在 \(2s-t=2\),\(-s+t=-1\)的位置
- 接出方程组就可以知道 \(O = (0, 1, 4)\)
- 从交点处在两个直线上衍生出两个 Vector,求他们的的 Cross Product 即为 Plane 的 Normal Vector
Equation of a Line Formed by the Intersection of Two Planes #
- 两个 \(\mathbb R^3\) 中的 Plane 的 Intersection 会是一个 Line,想要求的这个 Line 的 Equation
- 先通过两个 Plane 的 Normal Vector Cross 出 Intersection 的方向,再求出 Intersection 上任意一点
- 最后就可以得到 Line 的 Equation
Introduction to Multivariable Functions #
- Multivariable Functions 指的就是存在不止一个变量的 Function
- 其 Explicit function 显式函数为 \(z = f(x, y) = x² + y²\)
- 写成 Implicit function 隐式函数后则有 \(x² + y² − z = F(x, y, z) = 0\)
含义:把等式写成 F = 0 的形式,其中 F(函数)同时包含 x、y、z,未把 z 单独解出
- 但并不是所有的 Implicit Function 的 Explicit 都是很容易解出的,比如 Function
$$ sin(xyz) − zx + yx = F(x, y, z) = 0 $$
- 这个等式无法通过代数运算把 z 写成 z = f(x, y) 的形式
Domain and Range of Function #
- Consider 2 independent variables x and y and the function z = f(x, y)
- Domain(定义域):permissible values that you can input into the function
- Range(值域):all values that are outputs
- 对于 Domain 和 Range 来说,正确的书写表达很重要,拿函数 \(z = f(x,y) = \sqrt{4 - x^{2} - y^{2}}\) 举例,它的 Domain 和 Range 即为
| domain | range |
|---|---|
| \({(x,y);; x^{2}+y^{2}\le 4,\ (x,y)\in\mathbb{R}^{2}}\) | \(0 \le z \le 2,\ z \in \mathbb{R}\) |
Graphing 2-Variable Scalar Functions (Traces) #
- 首先,Traces 指的是 Cross sectional slice of a 3D shape

- 比如上图中的红色曲线就是这个 Ellipsoid 椭球 和 xy-Plane 的 Intersection,整个完整的曲线也就被称为 Trace
- 一般来说,Trace 并不单独出现,为了构建一个三位图形的骨架,需要构建多个二维对象
- 追常见的做法就是在 xy, xz, yz 三个 Plane 上切片,最终绘出完整的 3D 图像

Graphing 2-Variable Scalar Functions (Cylinders) #
- Definition: Cylinder(定义:柱面)
- 在三维空间中,一个二元函数的图形:Function 在 Missing Variable 的所有取值下都成立
- 换句话说,trace 在被忽略的变量方向上保持相同
- 举例来说,有 Function \(x^2+4y^2=16\),这个 Function 中完全不包含 z Axis 上的信息
- 分析它的 Domain 和 Range 来说,有
$$ { (x,y) ;|; x^2 + 4y^2 = 16, ; -4 \leq x \leq 4, ; -2 \leq y \leq 2, ; x,y \in \mathbb{R} } $$
$$ z \in \mathbb{R} $$
- 这意味着图形在 z 方向无限延伸 → 形成一个 cylinder(柱面)

Graphing 2-Variable Scalar Functions (Level Curves) #
- Level Curves 由多条线构成,在同一曲线上,所有点的高度相同
- 如果等高线很密集,表示高度变化快
- 如果等高线稀疏,表示高度变化慢
- 其完整的定义为:Level curves(等值曲线):把三维函数 \(z = f(x, y)\) 投影到 xy 平面,取不同的 z 常数值得到的曲线


Graphing Scalar 3-Variable Functions (Level Surfaces) #
- Level surfaces(等值面):是函数在不同常数值下的投影
- 给定函数 \(w = f(x,y,z)\),如果取 \(w = \text{constant}\),就能得到一个等值面
$$ w = f(x,y,z), \quad w = \text{constant} = f(x,y,z) $$

- 如图,不同的 w 值(常数)对应不同的曲面:
- w = 0(最内层)
- w = 1
- w = 2
- w = 3(最外层)
- 每一个 w = 常数,都代表一个具体的 surface(曲面)
- 当 w 增大时,等值面逐渐扩展,像一个逐层展开的锥形体