DS 1. Introductionto Logic Circuits
DS1.IntroductiontoLogicCircuits #
Last Edit: 10/2/25
计算机中的信息由 Electronic Signals 表示 ,其存在两个 Discrete Values,它们通过 Voltage Levels 电压电平实现,但是称为 Logic Values,0 和 1
2.1 Variables and Functions #
- Binary Circuits 在数字系统中占主导地位,因为他们简单,只允许两个可能值 0 和 1 的存在

- 这是最基本的形式,即一个 Switch,在其为 0 的时候灯为关闭的,在其为 1 的时候则是开启的
- 当把 Switch 添加到两个的时候,就会出现两种连接这两个 Switch 的方式,Series 和 Parallel,他们也将会产生不同的结果

- 在 Series 的时候,仅当 \(x_1 =x_2 =1\) 的时候 Light 是开的,同时也仅当 \(x_1=x_2=0\) 的时候 Light 是关的
- 在 Parallel 的情况下则不同

- 当 \(x_1 =1 | x_2=1\) 的情况下,Light 都是开的,同时 \(x_1 =x_2 =1\) 的时候 Light 也是开的
- 上面介绍了 Series 和 Parallel 的两种情况,同时也存在一种情况即两个同时出现,叫做 Series - Parallel Connection

- 如上图,Light 亮的情况下,需要 \(x_3= 1\) 的前提下,\(x_2\) 和 \(x_1\) 中起码有一个为 1
Logic Function 逻辑方程 #
- 总结上面的规律,可以总结一个表达式
- 用 + 表示 OR,用 $$ \(\cdot\) 表示 AND
- 在上面的 Series-Parallel Connection 中,则可以表达为
$$ L(x_1,x_2,x_3)=(x_1+x_2)+\cdot x_3 $$
- 需要注意不能把 +,\(\cdot\) 等逻辑运算符和加减乘除搞混
2.2 Inversion #
- 到目前为止,我们假设 switch closed 代表正向动作,比如灯亮
- 但同样有意义的是考虑另一种情况:当 switch opened 时触发动作
- 也就是和之前相反的情况,当 \(x=0\) 的时候 \(L=1\)
- 这个运算也叫做 NOT Operation 非运算
2.3 Truth Tables #
- 到目前已经介绍了三种最基本的逻辑运算,AND,OR 和 Complement,这些运算也可以通过 Table 的方式定义,具体方式是列出所有的可能性
- 这个 Table 则被称为 Truth Table

- 在少数变量的时候可以被很方便的列出来,但是一旦 Variable 数量增加后,表格的规模会 Exponentially Ascend
2.4 Logic Gates and Networks #
- 前面介绍的三种基本逻辑运算(AND、OR、NOT)都可以用来实现更复杂的 Logic functions 逻辑函数
- 每个逻辑运算都可以用 Transistors 晶体管 来实现,这样得到的电路元件叫做 logic gate逻辑门
- 一个逻辑门有一个或多个输入和一个输出,输出是输入的函数

- 上面的三个就是 Logic Gate 的 Schematic Diagram 原理图
- 注意到其中的符号 \(\cdot\), + 等,正如上面所提到的,一个 Logic Gate 存在多个 Input 和一个 Output
- 重新拿到之前的 Series-Parallel Connection

- 这个 Circuit Diagram 被画成 Schematic Diagram 后就是先是一个 OR Gate 后接一个 AND Gate

2.4.1 Analysis of A logic Network #
- 对于 Logic Network 来说,基本上存在两种问题
- 一个是 Analysis 分析,通过一个已知的网络,去确定他最终实现的逻辑功能
- 第二个则是 Synthesis 综合,设计一个新的 Logic Network 来实现某个功能
2.4.2 Exclusive OR (XOR) Function #
- 一个很常见的 Logic Circuit 是 XOR
- 信号 x 和 y 是电路的输入,电路控制一个灯 ****L
- 要求是:灯只有在两个开关中有一个(但不是两个同时)处于顶端时才点亮
这就是家中常见的控制灯的方式,当两个一样的时候灭灯,两个不一样的时候则是亮
- 具体来说:
- 当 x = 0, y = 1 时,L = 1(灯亮)
- 当 x = 1, y = 0 时,L = 1(灯亮)
- 其他情况下 L = 0
- 想要分析一个新的 Logic Circuit,第一步就是列出 Truth Table

- 在这种情况下分析灯亮的两种情况,即 \(\overline XY+X\overline Y\)
注意这里的 + 是 OR 的意思
- 于是就得到了最简单的 Function 形式

- 画成 Schematic Diagram 就是图 C 的样子
- 由于这是一个很常见的 XOR,所以单独为他设计了一个 Gate Symbol,即图 D
Design Example #
- 现在来一个更加复杂的情况
- 有一个生产线,其存在 3 个传感器,分别检测大小,光滑度和重量,当不达标的时候传感器为 0
- 当 3 个传感器中存在两个以上的 0 的时候,R = 1,即不通过
- 正如前面提到的,分析 Function 的第一步就是 Truth Table

- 本例子中的 Truth Table 应该长这样,分析其中 R = 1 时候的情况,可以得到

- 这里的关键就在于,+ 并不是再 Add,而是表示 OR
- 但是两个 OR 是可以相互组合的,比如 \(\overline s_0\overline s_1 \overline s_2\) 在这里就非常重要,因为它能和剩下的三个依次组合,完成化简
- 又因为 \(\overline s_n+s_n\) 无论如何都是 1 的特性,最终可以被化简到非常简单的形式
Timing Diagram #
- Timing Diagram 表示的是和 Truth Table 一样的信息,即在不同的信号下 Digit 的变化

- 上图就是 Exclusive OR(XOR)的 Timing Diagram
2.5 Boolean Algebra #
- Algebra 从 Axioms(公理)出发,他们是一套系统最初的假设,不需要证明就接受的命题

- \(\cdot\) 代表了 AND,0 和 0 做 AND,结果是 0,等
- 这几个就是最基本的 Boolean Algebra
Duality #
- Boolean Algebra 的一个特性,由于状态只有 0 和 1,所以当 Swap 一个 Axiom 的 0 和 1,同时更换 AND 和 OR 的时候,新的表达式仍将成立
- 于是上图中的蓝色就是通过 Axioms 的 Duality 总结出的
Single Variable Theorems #
- 在 Axioms 之上,可以总结出存在关于 Single Boolean Variable 的推论

- 他们同样有自己的 Axioms
Two and Three Variable Properties #
- 当处理两个或三个变量时也存在 Identities,常见的就是 Commutative, Associative 等

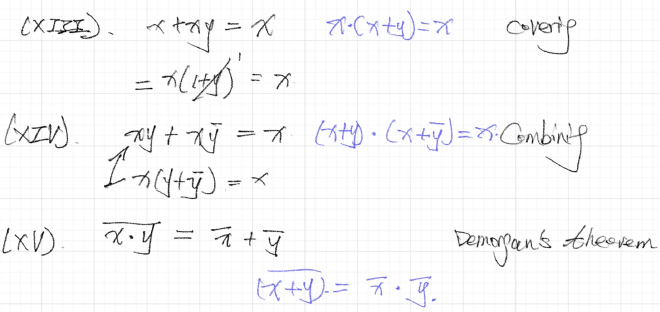
2.5.1 Venn Diagram #

- 通过 Shaded Area 表示 Set
Ex. Prove x + (yz) = (x + y)(x + z) #
- 第一种证法就是通过 Truth Table,这里主要讲的是 Venn Diagram

2.5.2 Notation and Terminology #
- 在 Boolean Algebra 中,分别使用 AND 和 OR 进行运算,而他们可以被用符号 \(\cdot\) 和 + 表示
- 因为 Boolean Algebra 和正常的 Algebra 中用的相同的符号,所以 AND 也被叫做 Logic Product,OR 则叫做 Logic Sum
- 于是就有了 Product of Sum 和 Sum of Product
- PoS 就是几个 OR 运算外面接了 AND,SoP 则相反
2.5.3 Precedence of Operations #
- 优先级在 Boolean Algebra 中并没有被明确规定
- 但是 Parentheses(括号)还是存在,用来指明运算顺序
- 但如果要避免过多的使用括号,也存在一个规定,先做 NOT,再是 AND,最后是 OR
AND 的乘号一般会被省略
2.6 Synthesis Using AND, OR, and NOT Gates #
2.6.1 Sum-of-Products and Product-of-Sums Forms #
Minterm #
-
定义是:A Product term that correspond to a row of a truth table
-
它是输出为 1 的时候的条件表达,这句话很关键
-
由于 Minterm 是 Product Term (AND Term),所以需要所有 Term 都为 1,即在 0 的 Term 上 Complement(取反)
-
当一个 Function 被写作是 \(\sum m(0,1,2)\) 就代表了第 0,1,2 行的 Truth Table 值为 1
-
而三个变量又确定了这是一个有着 \(2^3 = 8\) 行的 Truth Table,所以就是 000, 001, 010 三个 Term 为 1,而要让他们为 1,中间还是 Product (AND) 则 Conical SoP 为
$$ \overline{x_1},\overline{x_2}\overline{x_3},\overline{x_1},\overline{x_2},x_3,\overline{x_1},x_2,\overline{x_3} $$
Maxterm #
- 同理:A Sum term that correspond to a row of a truth table
- 他是输出为 0 时的条件表达,所以当存在任何一个 1 的时候,都要对他取 Complement

Cononical SoP #
- 一个 SoP Expression,其中每一个 Product 都是一个 Minterm
Cononical PoS #
- 同理:一个 PoS Expression,其中每一个 Sum 都是一个 Maxter
Duality #
- 由于 Boolean Algebra 的 Duality 特性,Min 和 Max term 也有着他们的 Duality
- 假设一个 Function \(f(x,y,z)\) 有 \(\sum m (0,1,6,7)\) 作为 Minterm,那根据 Duality 他就有 \(\prod M(2,3,4,5)\) 作为 Maxterm
Ex. Proof of Duality #
- 就拿上面的 \(\sum m(0,1,6,7)\) 举例,有
$$ f=(x+\overline y+z)\cdot(x+\overline y + \overline z)\cdot (\overline x+y+z)\cdot (\overline x+y+\overline z) $$
- 它的 Complement \(\overline f\) 就是 SoP,有
$$ \overline f= \overline xy\overline z+\overline xyz +x \overline y \overline z+x \overline yz $$
- 要通过 \(\overline f\) 计算 \(f\),就通过再次 Complement 就可以得到, 有
$$ \overline{\overline f} = f=\overline{\overline xy\overline z+\overline xyz +x \overline y \overline z+x \overline yz} $$
- 回顾 Demorgan’s Theorem,\(\overline {x_1x_2}=\overline{x_1}+\overline{x_2}\),\(\overline{x_1+x_2}=\overline{x_1}\cdot \overline{x_2}\)
- 在上面的 \(\overline{\overline f}\) 中,先使用第二个得到
$$ f=\overline{\overline xy\overline z}\cdot \overline{\overline xyz}\cdot \overline{x\overline y z}\cdot \overline{x \overline y z} $$
- 再用第一个得到
$$ f=(x+\overline y +z)\cdot ( x+\overline y + \overline z)\cdot (\overline x+y+\overline z)\cdot(\overline x+y+\overline z) $$
- 注意到这和上面的 PoS 是一个东西了