AEM 1. Complex Numbers
AEM1.ComplexNumbers #
Last Edit:9/15/25
Complex Numbers #
- 最早对 Complex Numbers 的接触出现在 Quadratic Equation 中
- 当有 \(ax^2+bx+c=d\) 的时候,如果 Discriminant 判别式 \(b^2-4ac < 0\) 的时候,方程没有 Real Solution,这时候就引入了 Imaginary Unit \(i^2=-1\)
- 但是同时一个 Complex Number 并不止含有 Imaginary Unit,它同时包含 Real Part,于是就可以定义一个完整的 Complex Number 为任意形式的
$$ \mathbb C={z|z=a+bi,a,b\in\mathbb R } $$
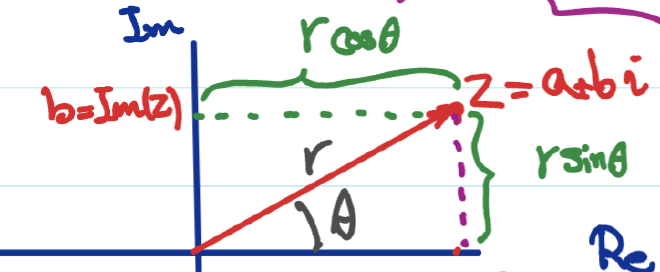
- 其也有 Polar Form,也称为三角形式,为
$$ z=r(\cos \theta+i\sin\theta) $$
Arithmetic Operations #
- Complex Number 的加减乘除如下
- 设 \(z_1 = x_1 + iy_1, z_2 = x_2 + iy_2\):
Addition #
$$ z_1 + z_2 = (x_1 + x_2) + i(y_1 + y_2) $$
Subtraction #
$$ z_1 - z_2 = (x_1 - x_2) + i(y_1 - y_2) $$
Multiplication #
$$ z_1 z_2 = (x_1x_2 - y_1y_2) + i(x_1y_2 + x_2y_1) $$
Division #
- 在计算 Complex Number 的 Division 之前需要先定义 \(z^{-1}\)
- 这个数他需要满足的条件为 \(z\times z^{-1} =1\)
- 现在已知 \(z=a+bi\),可以计算出 \(z^{-1}\) 的 Rectangular Form 为#
$$ \frac1z= \frac{1}{a+bi}=\frac{1}{a+bi}\times\frac{a-bi}{a-bi}=\frac{a-bi}{a^2+b^2}=\frac{a}{a^2+b^2}-i\cdot\frac{b}{a^2+b^2} $$
Conjugate #
- Complex Number 的 Conjugate 的定义就是
$$ \overline Z = Re(z)-iIm(z) $$
- 定义好了 Conjugate 的特性,就会出现很多二级结论
$$ \frac{1}{z} = \frac{1}{z} \times \frac{\overline{z}}{\overline{z}}= \frac{\overline{z}}{z \overline{z}}= \frac{\overline{z}}{|z|^2} $$
$$ \overline{z} |= \sqrt{(\operatorname{Re}(z))^2 + (-\operatorname{Im}(z))^2}= |z| $$
$$ \left| \frac{1}{z} \right|= \left| \frac{\overline{z}}{|z|^2} \right|= \frac{1}{|z|^2} |\overline{z}|= \frac{1}{|z|^2} |z|= \frac{1}{|z|} $$
$$ z\overline{z} = (\operatorname{Re}(z) + \operatorname{Im}(z) i)(\operatorname{Re}(z) - \operatorname{Im}(z) i) = (\operatorname{Re}(z))^2 + (\operatorname{Im}(z))^2 = |z|^2 $$
$$ \frac{z + \overline{z}}{2} = \operatorname{Re}(z) $$
$$ \overline{z_1 + z_2} = \overline{z_1} + \overline{z_2} $$
$$ \overline{z_1 z_2} = \overline{z_1} , \overline{z_2} $$
$$ \overline{\left(\frac{z_1}{z_2}\right)} = \frac{\overline{z_1}}{\overline{z_2}} $$
Polar Form #
- 现在研究几个 Polar Form 下的结论
- 假设现在有 \(z=r(\cos\theta+i\sin\theta)\)
- Find Polar Form of \(\overline z\)
$$ \overline{Z} = r(\cos\theta - i \sin\theta) = r(\cos(-\theta) + i\sin(-\theta)) $$
- Find Polar Form of \(\frac1z\)
$$ \frac{1}{Z} = \frac{1}{|Z|^2} , \overline{Z} = \frac{1}{r^2} , r(\cos(-\theta) + i \sin(-\theta)) = \frac{1}{r} \left( \cos(-\theta) + i \sin(-\theta) \right) $$
Geometric Interpretation #
- 假设有一个 \(z = a + bi\),What is the geometric interpretation of \(\overline z\) and \(\frac1z\)

- 根据上面 Polar Form 中得到的结论可以看出,Conjugate 和 Reciprocal 的 Mod 和 Argument
Multiplication by i #
- 当一个 Complex Number 乘上一个 Imaginary Number i 的时候,本质上就是将其 Polar Form 的图案 CCW 移动了 90 Degree

- 同时,当两个 Complex Number 互乘的时候,他们的结果如下
$$ Z_1 Z_2 = r_1 \bigl( \cos\theta_1 + i \sin\theta_1 \bigr) \times r_2 \bigl( \cos\theta_2 + i \sin\theta_2 \bigr) \[6pt]= r_1 r_2 \left( \bigl( \cos\theta_1 \cos\theta_2 - \sin\theta_1 \sin\theta_2 \bigr) + i \bigl( \cos\theta_1 \sin\theta_2 + \sin\theta_1 \cos\theta_2 \bigr) \right) \[6pt]= r_1 r_2 \left( \cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2) \right) $$
- 观察公式可以看出,Multiplication 的结果就是,mod 相乘,Argument 相加
Argument 辐角 #
- Complex Number 中,Argument 是指复数在复平面上与 正实轴 的夹角
- 假设现在有 \(z = (-2.5)\left(\sin\frac{\pi}{7} - i\cos\frac{\pi}{7}\right)\),要求 Z 的极坐标形式,有
$$ z = 2.5\left(-\sin\frac{\pi}{7} + i\cos\frac{\pi}{7}\right) $$
- 注意到 \(\sin\) 和 \(\cos\) 的位置不对,通过三角公式可以变换求得 \(\theta\)

Principle Argument #
- Principle Argument 就是最简单的那个 Argument,取值范围是
$$ -\pi < \arg(z) \leq \pi $$
Ex. #

Complex Exponential #
- We define \(e^z\) for any \(z \in \mathbb{C}\) with the same series:
$$ e^z = \sum_{n=0}^{\infty} \frac{z^n}{n!} $$
- 上面的公式就是 Definition of exponential function in complex domain(复数域中的指数函数定义)
Properties #
- 复数域中指数函数的几个重要性质:
Property #1 #
$$ e^{z_1 + z_2} = e^{z_1} \cdot e^{z_2}, \quad \forall z_1, z_2 \in \mathbb{C} $$
- 指数加法法则,在复数域中依然成立
Property #2 #
$$ e^0 = 1 $$
- 零次幂等于 1
Property #3 #
$$ e^{-z} = \frac{1}{e^z}, \quad \forall z \in \mathbb{C} $$
- 负指数等于倒数
Property #4 #
$$ (e^z)^k = e^{kz}, \quad \forall z \in \mathbb{C}, ; k \in \mathbb{Z} $$
- 整数次幂的性质
Euler’s Formula #
- 令 \(z = i\theta\),代入指数函数的定义:
$$ e^{i\theta} = \sum_{n=0}^{\infty} \frac{(i\theta)^n}{n!} $$
- 把各项展开,可以分为:
- 实部(Real part):\(1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} - \dots = \cos \theta\)
- 虚部(Imaginary part): \(i(\theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \dots) = i\sin \theta\)
- 于是就有
$$ e^{i\theta} = \cos\theta + i\sin\theta $$
Geometric meaning #
- 前面提到了 Euler’s Formula 指出了 \(e^{i\theta} = \cos\theta + i\sin\theta\),这就说明了 \(e^{i\theta}\) 是在 unit circle 上的一个复数,Arugument 为 \(\theta\)
Properties #
- \(|e^{i\theta}| = 1\),因为 \(\cos^2\theta + \sin^2\theta = 1\)
- 回忆 mod 的定义 对于 Complex Number \(z = x+iy\) 来说,它的 mod \(|z| = \sqrt{x^2 + y^2}\)
- 套用到 \(e^{i\theta}\) 中可以得到 \(|e^{i\theta}| = \sqrt{(\cos\theta)^2 + (\sin\theta)^2}=1\)
- \(\arg(e^{i\theta}) = \theta + 2k\pi, , k \in \mathbb{Z}\)
Polar Representation #
- 复数的极坐标表示:
$$ Z = r(\cos\theta + i\sin\theta) $$
- 这里 r 是模(modulus)
- \(\theta\) 是辐角(argument)
Exponential Representation #
- 利用欧拉公式,可以写成:
$$ Z = re^{i\theta}= re^{i(\theta + 2k\pi)}, \quad \forall k \in \mathbb{Z} $$
Euler’s Identity #
- 上面的 Euler’s Formula 写道
$$ e^{i\theta} = \cos\theta + i\sin\theta $$
- 当 \(\theta = \pi\) 时:
$$ e^{i\pi} = \cos\pi + i\sin\pi $$
- 将值代入,有 \(\cos\pi = -1, \quad \sin\pi = 0\),可以得到
$$ e^{i\pi} = -1 + i\cdot 0 = -1 $$
- 于是就得到了 Euler’s Identity
$$ e^{i\pi} + 1 = 0 $$
Euler’s Formula + Rectangular Representation #
- 回顾指数的性质 Recall property #1
$$ e^{z_1 + z_2} = e^{z_1} \cdot e^{z_2} $$
- 把复数写成 Rectangular form,令
$$ Z = x + iy, \quad x,y \in \mathbb{R} $$
- 于是就有
$$ e^Z = e^{x+iy}= e^x \cdot e^{iy} $$
- 根据 Euler’s Formula 可以知道
$$ e^{iy} = \cos y + i\sin y $$
- 再乘上 \(e^x\) 可以得到
$$ e^{x+iy} = e^x (\cos y + i\sin y) $$
- 这就是复数指数函数的 Rectangular representation 直角坐标表示
Upshot #
- 由上式可以得到几个重要结果:
Modulus #
$$ |e^Z| = e^x $$
Argument #
$$ \arg(e^Z) = y + 2k\pi, \quad k \in \mathbb{Z} $$
- 如果有两个复数 \(Z_1, Z_2\):
$$ \arg(Z_1 Z_2) = \arg(Z_1) + \arg(Z_2) $$
Integer Powers of Complex Numbers #
- 很多我们用三角函数证明过的复数性质,其实也可以用指数函数来证明
Multiplication of complex numbers 复数相乘的性质 #
- 之前提到
$$ Z_1 Z_2 = r_1 r_2 \big(\cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2)\big) $$
- 换成指数形式:
$$ Z_1 = r_1 e^{i\theta_1}, \quad Z_2 = r_2 e^{i\theta_2} $$
- 那么:
$$ Z_1 Z_2 = r_1 e^{i\theta_1} \cdot r_2 e^{i\theta_2} = r_1 r_2 e^{i(\theta_1 + \theta_2)} $$
- 再用 Euler’s Formula 可以得到:
$$ = r_1 r_2 (\cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2)) $$
- 这和三角函数的方法一致,但更简洁
De Moivre’s Formula(棣莫弗公式) #
- 由指数函数的性质:
$$ (e^{i\theta})^n = e^{in\theta}, \quad n \in \mathbb{Z} $$
- 于是:
$$ (\cos\theta + i\sin\theta)^n = (e^{i\theta})^n=(e^{i n\theta })=\cos(n\theta) + i\sin(n\theta) $$
- 这就是著名的 De Moivre’s Formula
Integer powers of complex numbers 复数的整数次幂 #
- 设复数:\(Z = |Z| e^{i\theta}\)
- 给定整数 kk:
$$ Z^k = (|Z| e^{i\theta})^k = (|Z|)^k e^{ik\theta} = |Z|^k (\cos(k\theta) + i\sin(k\theta)) $$
- Modulus:被提升到 k 次方,变为 \(|Z|^k\)
- Argument:被放大 k 倍,变为 \(k\theta\)
- 也就是说:复数的幂就是“拉伸模长 + 放大角度”
Ex. #

- B 和 C 正确没什么特别的,对于 E 来说 \(\frac{3\pi}{4}=-\frac{5\pi}{4}\) 也没问题
- 对于 F 来说就是多了一个 \(2\pi\),也没问题
Roots of Complex Numbers #
- 如果 w 是 Z 的 n 次方根,记作
$$ Z^{1/n} = w, \quad \text{if } w^n = Z $$
- 将他们两个写成 Exponential 的形式,有
$$ Z = r_0 e^{i\theta_0}, \quad w = r e^{i\theta} $$
- 要求 \(w^n = Z\),即
$$ (r e^{i\theta})^n = r^n e^{i n\theta} = r_0 e^{i\theta_0} $$
- 根据 Complex Exponential 的性质,可以得到
- 模长:
$$ r^n = r_0 ;;\Rightarrow;; r = (r_0)^{1/n} $$
- 角度:
$$ n\theta = \theta_0 + 2k\pi, \quad k \in \mathbb{Z}\Rightarrow \theta = \frac{\theta_0 + 2k\pi}{n} $$
- 通得到 General Solution
$$ w = r_0^{1/n} e^{i\frac{\theta_0+2k\pi}{n}}, \quad k \in \mathbb{Z} $$
- 注意:一共有恰好 n 个不同的 Complex Roots
Geometric Interpretation #
Roots on a circle #
- 所有根都在一个圆上,其半径为
$$ |Z|^{1/n} = r_0^{1/n} $$
Even spacing #
- 这些根沿着圆 平均间隔 \(2\pi/n\),起点在 \(\theta_0/n\)
$$ w_k = Z^{1/n} = r_0^{1/n} e^{i\frac{\theta_0+2k\pi}{n}}, \quad k=0,1,2,\dots,(n-1) $$
Ex. 求 \(\sqrt{i}\) #
- 先写出 i 作为一个 Complex Number 的 Exponential Form,有 \(i = e^{i\pi/2}\)
- 平方根:
$$ w = e^{i(\pi/2 + 2k\pi)/2}, \quad k=0,1\Rightarrow w_1 = e^{i\pi/4}, \quad w_2 = e^{i(5\pi/4)} $$

- 在图上,两个根分布在圆上,相隔 \(\pi\)(180°)
Complex Logarithm #
- 令 \(w = \ln Z \Rightarrow Z = e^w\)
- 这是 Complex Logarithm 的定义方式,即如果我们要定义 \(w = \ln Z\),那就要让 \(Z = e^w\) 成立
- 为了找出 w,我们令复数 \(Z = x + iy = re^{i\theta}\)
两个分别是 Rectangular Form 和 Polar Form
- 假设 \(w(x,y) = U(x,y) + iV(x,y)\),这里表示将 w 写成 Real + Imaginary 的形式,也就有
$$ e^{w(x,y)} = e^{U(x,y) + iV(x,y)} = e^{U(x,y)} \cdot e^{iV(x,y)} $$
- 这个东西是等于 \(Z = re^{i\theta}\) 的,这就可以将他们一一对应,得到
$$ e^{U(x,y)} = r \Rightarrow U(x,y) = \log_e r = \log_e |Z| $$
- 于是就可以得到 General Solution 形式
$$ \ln(Z) = \log_e |Z| + i(\theta + 2\pi k),\quad k \in \mathbb{Z} $$
上面的意思就是,给定一个 \(Z\in \mathbb C\),\(\ln(Z)\) 存在无数个 Periodic Solutions

- 其中每一个 Solution 之间间隔 \(2\pi\)
ln is a Multi-Valued Function #
- 由于一个 Complex Number 存在无限个周期性的 Argument,这就是导致 Complex Logarithm 存在无限解的原因,同时 \(\ln Z\) 就可以写成
$$ \ln(Z)=\log_e|Z|+i\arg(Z) $$
- 同时就也会存在一个 Principle Argument Arg(z),写做
$$ Ln(Z)=\log_e|Z|+iArg(Z) $$
Properties of \(e^z\) and \(ln(z)\) #
- 设现在有 Complex Number \(z = x + iy\),可以得到以下性质
- \(|e^z| = e^x\),模长等于实部的指数
- \(\arg(e^z) = y + 2\pi k,k \in \mathbb{Z}\),幅角来自虚部
- 同时,由于 Complex Logarithm 的 Solution 是一个 Set
$$ \ln(z) = { w \mid e^w = z } $$
- 所以有:
- \(e^{\ln(z)} = z\),只要 \(z \neq 0\)
- 如果 \(w_1 \in \ln(z_1), w_2 \in \ln(z_2)\),那么 \(w_1 + w_2 \in \ln(z_1 z_2)\)
只在复数对数的多值定义下成立,不适用于 Principal value
- 其实就是
$$ \ln(z_1) + \ln(z_2) = \ln(z_1 z_2) $$
- 于是可以 Derive 出
$$ \ln\left(\frac{1}{z}\right) = -\ln(z), \quad\ln\left(\frac{z_1}{z_2}\right) = \ln(z_1) - \ln(z_2) $$
Ex. 1 ln(3) #
- 先说结论,\(ln(3)\) 就是 \(log_e(3)\)
- 具体带入公式可以得到 3 的 Mod 为 3,Arg 为 0,于是有
$$ \ln(3) = \log_e |3| + i\arg(3) = \log_e 3 $$
Ex. 2 ln(−3) #
- \(\ln(-3)\) 就和上面的不一样了,在 Real Analysis 中,Logarithm 中是不允许出现负数的,但是在 Complex Analysis 中,有
$$ \ln(-3) = \log_e |-3| + i\arg(-3) = \log_e 3 + i\pi $$
- 详细来说,-3 的 mod 为 3,Arg 为 \(\pi\)
求解 e^z = 1 + i #
- 两边取对数就可以知道这题在问的是 \(Z = \ln(1 + i)\) 的解,有
$$ Z = \ln(1 + i) = \log_e \sqrt{2} + i\left( \frac{\pi}{4} + 2\pi k \right), \quad k \in \mathbb{Z} $$
- 用图表示这个解就是

- 用图画出所有解在复平面上的位置就有,将 Real Part 固定:\(\log_e \sqrt{2}\),将 Imagery Part 周期性上移:\(\frac{\pi}{4} + 2\pi k\)
- 最终得到一条沿虚轴等间距排列的点列
General Complex Power #
- 想要定义 \(Z^α\),\(\text{其中 } Z, \alpha \in \mathbb{C}\)
- 类似于实数域中 \(x^a\),我们在复数域中定义:
$$ Z^\alpha = e^{\alpha \cdot \ln(Z)} $$
Ex. 1: \(2^\pi\) #
$$ 2^\pi = e^{\pi \cdot \ln(2)} $$
- 右边使用公式 \(e^{\alpha \ln Z}\)
- 现在分析 Complex logarithm \(\ln 2\),有
$$ \ln(2) = \log_e 2 + i \cdot 2\pi k $$
2 的 Arg (Principle Argument) 是 0,但是 arg 不是
- 乘以 \(\pi\) 得到:
$$ \pi \log_e 2 + i \cdot 2\pi^2 k $$
- 指数展开为:
$$ e^{\pi \log_e 2} \cdot e^{i \cdot 2\pi^2 k} = 2^\pi \cdot e^{i \cdot 2\pi^2 k} $$
- 最后写成:
$$ 2^\pi = 2^\pi \angle 2\pi^2 k $$
- 意思是模长为 \(2^\pi\),虚部会旋转 \(2\pi^2 k\)
Ex. 2: \(i^i\) #
- 已知 \(i^i = e^{\ln(i) \cdot i}\)
$$ \ln(i) = \log_e 1 + i \cdot \arg(i) = 0 + i\left( \frac{\pi}{2} + 2\pi k \right) $$
- 所以:
$$ i^i = e^{i \cdot i \cdot \left( \frac{\pi}{2} + 2\pi k \right)} = e^{- \left( \frac{\pi}{2} + 2\pi k \right)} $$
- 它的 Principle Branch 就是
$$ i^i = e^{-\pi/2} \quad \text{(当选择主值 (k = 0) 时)} $$
Jacques Hadamard #
“The shortest path between two truths in the real domain passes through the complex domain.“ —— 在实数域中,两条真理之间最短的路径,是通过复数域。
- 现在需要证明
$$ \cos A \cos B = \frac{1}{2} \left[ \cos(A+B) + \cos(A-B) \right] $$
- 首先用 Euler‘s 表示 cos 和 sin
$$ \cos x = \frac{e^{ix} + e^{-ix}}{2}, \quad \sin x = \frac{e^{ix} - e^{-ix}}{2i} $$
- 把 \(\cos A \cos B\) 用复指数展开:
$$ \begin{align*}\cos A \cdot \cos B &= \left( \frac{e^{iA} + e^{-iA}}{2} \right) \cdot \left( \frac{e^{iB} + e^{-iB}}{2} \right) \&= \tfrac{1}{4} \left( e^{i(A+B)} + e^{i(A-B)} + e^{-i(A-B)} + e^{-i(A+B)} \right)\end{align*} $$
- 利用对称性重新组合:
$$ e^{i(A+B)} + e^{-i(A+B)} = 2\cos(A+B) $$
$$ e^{i(A-B)} + e^{-i(A-B)} = 2\cos(A-B) $$
- 最终得到
$$ \cos A \cdot \cos B = \frac{1}{2} \left[ \cos(A+B) + \cos(A-B) \right] $$
Defining Complex Trigonometric Functions #
- 回顾 Euler’s Formula,有
$$ e^{i\theta} = \cos\theta + i\sin\theta $$
-
可以得出:
$$ \sin\theta = \frac{e^{i\theta} - e^{-i\theta}}{2i}, \quad \cos\theta = \frac{e^{i\theta} + e^{-i\theta}}{2} $$
-
现在想要定义 \(\sin(z),\cos(z)\) 在复数 \(z \in \mathbb{C}\) 中怎么定义
-
Definition 就是直接先把 Complex Number z 替换进去,可以得到
$$ \sin(z) = \frac{e^{iz} - e^{-iz}}{2i},\quad \cos(z) = \frac{e^{iz} + e^{-iz}}{2} $$
- 然后对 tan 和 cot 同理
$$ \tan(z) = \frac{\sin(z)}{\cos(z)}, \quad \forall z \in \mathbb{C}, \cos(z) \ne 0 $$
$$ \cot(z) = \frac{\cos(z)}{\sin(z)}, \quad \forall z \in \mathbb{C}, \sin(z) \ne 0 $$
Hyperbolic Sine #
- 双曲正弦函数 \(\sinh x\) 是和单位双曲线 \(x^2-y^2=1\) 有关的正弦函数,定义为
$$ \sinh(x) = \frac{e^x - e^{-x}}{2}, \quad\cosh(x) = \frac{e^x + e^{-x}}{2} $$

- 同理,Complex Number 下的 \(\sinh z\) 就是把 z 先带入
$$ \sinh(z) = \frac{e^z - e^{-z}}{2}, \quad \forall z \in \mathbb{C} $$
$$ \cosh(z) = \frac{e^z + e^{-z}}{2}, \quad \forall z \in \mathbb{C} $$
Summarize #
| 函数名 | 定义公式 |
|---|---|
| \(\sin(z)\) | \(\frac{e^{iz} - e^{-iz}}{2i}\) |
| \(cos(z)\cos(z)\) | \(\frac{e^{iz} + e^{-iz}}{2}\) |
| \(\tan(z)\) | \(\frac{\sin(z)}{\cos(z)}, 条件:\cos(z) \ne 0\) |
| \(\cot(z)\) | \(c\frac{\cos(z)}{\sin(z)}, 条件:s\sin(z) \ne 0\) |
| \(\sinh(z)\) | \(\frac{e^z - e^{-z}}{2}\) |
| \(\cosh(z)\) | \(\frac{e^z + e^{-z}}{2}\) |
Properties of Complex Trig Functions #
- 下面要介绍几个在 Complex Domain 下的 Trig 的 Properties
Sin(z) & Cos(z) in Rectangular Form #
-
先定义一个 Complex Number \(z = x + i y\),其中 \(x, y \in \mathbb R\)
-
已知 Complex sine function 为
$$ \sin(z) = \frac{e^{iz} - e^{-iz}}{2i} $$
-
将完整的 z 带入,得到
$$ \sin(z) = \frac{e^{i(x+iy)} - e^{-i(x+iy)}}{2i} $$
- 已知 Euler’s Formula
$$ e^{ix} = \cos x + i \sin x, \quad e^{-ix} = \cos x - i \sin x. $$
- 代入得到
$$ \sin(x+iy) = \frac{e^{-y}(\cos x + i \sin x) - e^{y}(\cos x - i \sin x)}{2i}. $$
- 展开公式得到
$$ = \frac{(e^{-y}\cos x + i e^{-y}\sin x) - (e^{y}\cos x - i e^{y}\sin x)}{2i} $$
$$ = \frac{(e^{-y}\cos x - e^{y}\cos x) + i(e^{-y}\sin x + e^{y}\sin x)}{2i} $$
- 将两个分子分离,
$$ \frac{e^{-y}\cos x - e^{y}\cos x}{2i} = \frac{- (e^{y}-e^{-y})\cos x}{2i} $$
$$ \frac{1}{i} = -i, \quad \frac{e^{y} - e^{-y}}{2} = \sinh(y) $$
- 所以得到:
$$ = i \cos(x) \sinh(y) $$
- 另外一半有
$$ \frac{i(e^{-y}\sin x + e^{y}\sin x)}{2i} = \frac{e^{y}+e^{-y}}{2} \sin x. $$
$$ \frac{e^{y}+e^{-y}}{2} = \cosh(y) $$
- 所以得到
$$ = \sin(x) \cosh(y) $$
- 最后把两个加一块得到
$$ \sin(x+iy) = \sin(x)\cosh(y) + i \cos(x)\sinh(y) $$
- cos 有类似的结论
$$ \cos(z) = \cos(x)\cosh(y) - i \sin(x)\sinh(y) $$
sin(z) & sinh(z) #
- 已知 sin z 和 sinh z 的 Formula
$$ \sin(z) = \frac{e^{iz} - e^{-iz}}{2i}, \quad \sinh(z) = \frac{e^z - e^{-z}}{2} $$
-
代入 \(z \to i z\):
$$ \sinh(i z) = \frac{e^{iz} - e^{-iz}}{2} = i \sin(z) $$
-
所以得到关系:
- \(\sinh(z) = i \sin(i z)\)
- \(\sin(z) = -i \sinh(i z)\)
-
对于 Cos 也有类似结论,
- \(\cos(i z) = \cosh(z)\)
- \(\cosh(i z) = \cos(z)\)
Modulus of sin z and cos z #
- 根据上面的结论
$$ \sin(z) = \sin(x)\cosh(y) + i \cos(x)\sinh(y) $$
- 所以模平方为
$$ |\sin(z)|^2 = (\sin(x)\cosh(y))^2 + (\cos(x)\sinh(y))^2 $$
- 展开得到
$$ |\sin(z)|^2 = \sin^2(x)\cosh^2(y) + \cos^2(x)\sinh^2(y) $$
- 已知
$$ \cosh^2(y) = 1 + \sinh^2(y) $$
- 代入得到
$$ |\sin(z)|^2 = \sin^2(x) + \sinh^2(y) $$
- cos 也有相同结论
$$ |\cos(z)|^2 = \cos^2(x) + \sinh^2(y) $$
Zeros of sin(z) and cos(z) #
- 当一个 Complex Trig Function 想要成为 Zero 的时候,Complex number 也有固定值
$$ \sin(z) = 0 \iff \sin^2(x) + \sinh^2(y) = 0 $$
- 因为平方和为零,必须同时成立:
$$ \sin(x) = 0, \quad \sinh(y) = 0 $$
- \(\sin(x) = 0 \implies x = k\pi, ; k \in \mathbb{Z}\)
- \(\sinh(y) = 0 \implies y = 0\)
- 所以:
$$ \sin(z) = 0 \iff z = k\pi, \quad k \in \mathbb{Z} $$
- 对于 Cos 有着类似结论
$$ \cos(z) = 0 \iff \cos^2(x) + \sinh^2(y) = 0 $$
- 同样必须同时成立:
$$ \cos(x) = 0, \quad \sinh(y) = 0 $$
- \(\cos(x) = 0 \implies x = \frac{(k+1)\pi}{2}, ; k \in \mathbb{Z}\)
- \(\sinh(y) = 0 \implies y = 0\)
$$ \cos(z) = 0 \iff z = \frac{(k+1)\pi}{2}, \quad k \in \mathbb{Z} $$
Periodicity of sin(z), cos(z), sinh(z) and cosh(z) #
Sin(z) & Cos(z) #
- 先说结论,sin(z) 和 cos(z) 的 Period 就是 \(2\pi\),而 sinh(z) 和 cosh(z) 的 Period 为 \(2\pi i\)
$$ \sin(z) = \frac{e^{iz} - e^{-iz}}{2i}, \quad \cos(z) = \frac{e^{iz} + e^{-iz}}{2}. $$
- 把 \(z \to z + 2\pi\):
$$ \sin(z+2\pi) = \frac{e^{i(z+2\pi)} - e^{-i(z+2\pi)}}{2i} $$
- 因为
$$ e^{i(z+2\pi)} = e^{iz} e^{i2\pi} = e^{iz} \cdot 1 = e^{iz} $$
$$ e^{-i(z+2\pi)} = e^{-iz} e^{-i2\pi} = e^{-iz} \cdot 1 = e^{-iz} $$
- 所以:
$$ \sin(z+2\pi) = \frac{e^{iz} - e^{-iz}}{2i} = \sin(z) $$
- 有相同结论
$$ \cos(z+2\pi) = \cos(z) $$
- 所以 \(\sin(z)\) 和 \(\cos(z)\) 的周期是 \(2\pi\)
sinh(z) and cosh(z) #
$$ \sinh(z) = \frac{e^z - e^{-z}}{2}, \quad \cosh(z) = \frac{e^z + e^{-z}}{2}. $$
- 把 \(z \to z + 2\pi i\)
$$ \sinh(z+2\pi i) = \frac{e^{z+2\pi i} - e^{-(z+2\pi i)}}{2}. $$
$$ = \frac{e^z e^{2\pi i} - e^{-z} e^{-2\pi i}}{2}. $$
- 因为 \(e^{2\pi i} = 1, ; e^{-2\pi i} = 1\),所以:
$$ \sinh(z+2\pi i) = \frac{e^z - e^{-z}}{2} = \sinh(z) $$
同理:
$$ \cosh(z+2\pi i) = \cosh(z) $$
- 所以最终得出 \(\sinh(z)\) 和 \(\cosh(z)\) 的周期是 \(2\pi i\)

- 还有很多和 Real Number 中相同的结论
Ex. Find Z s.t. Cos(z) = Sin(z) #
$$ \frac{e^{iz} + e^{-iz}}{2} = \frac{e^{iz} - e^{-iz}}{2i} $$
$$ i(e^{iz} + e^{-iz}) = e^{iz} - e^{-iz}\Rightarrow(i-1)e^{iz} = -(i+1)e^{-iz}\Rightarrow e^{2iz} = \frac{-(i+1)}{i-1} $$
- 化简得到 \(e^{2iz} = i\),取对数:\(2iz = \ln(i)\)
- 得到 \(\ln(i) = i\left(\frac{\pi}{2} + 2k\pi\right), \quad k \in \mathbb{Z}\)
- 解出 z 为 \(z = \frac{\pi}{4} + k\pi, \quad k \in \mathbb{Z}\)