Last Edit: 10/24/24
Introduction to Determinate
#
行列式是一个每个方阵都具有的数值
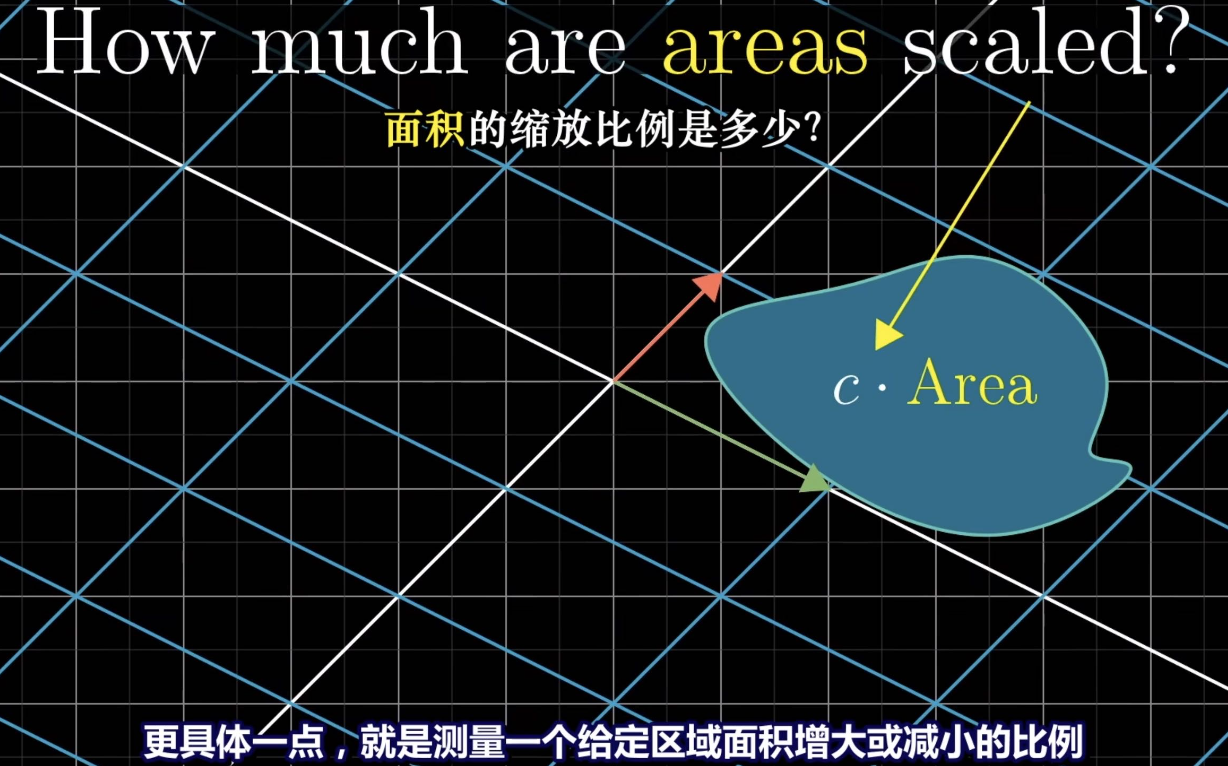
Determinate measures the factor by which the area of a given region increases or decreases
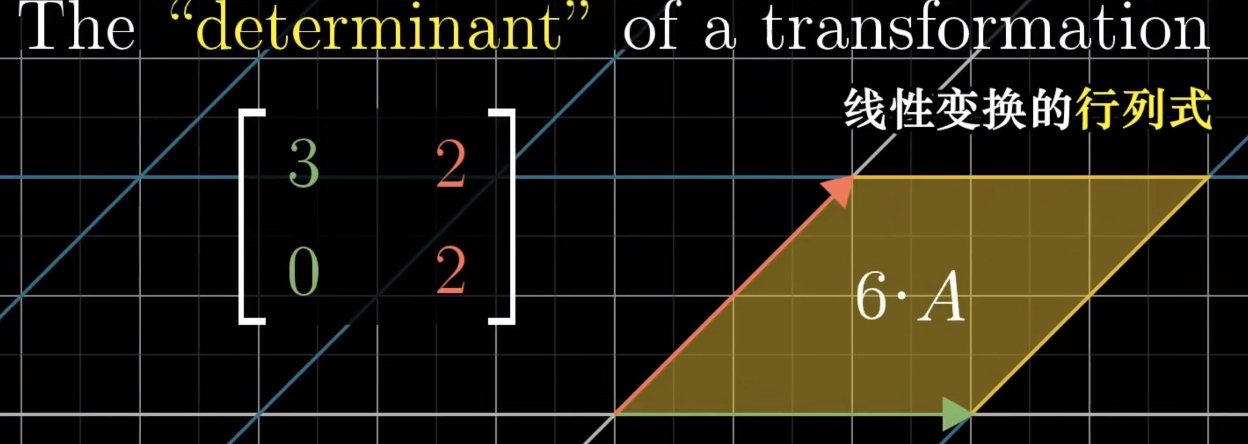
The “determinant” of a transformation
Determinate in R^2
#
Determinant计算的是Linear Transformation改变的Basis Vector所围成的面积的大小
而对于一个Linear Transformation,大部分情况下Basis Vector围成的面积都是一个长方形
而[[MAT188 Chapter 2 Linear Transformations#2.2 Linear Transformations in Geometry]]中存在一种Sheer Transformation,即对于一个Basis Vector来说,其出现了不属于其方向上的分量
如上图中的\(\vec e_2\)来说,其为<2,2>,即产生了Sheer
在这种情况下,所围成的面积便成为了Parallelogram
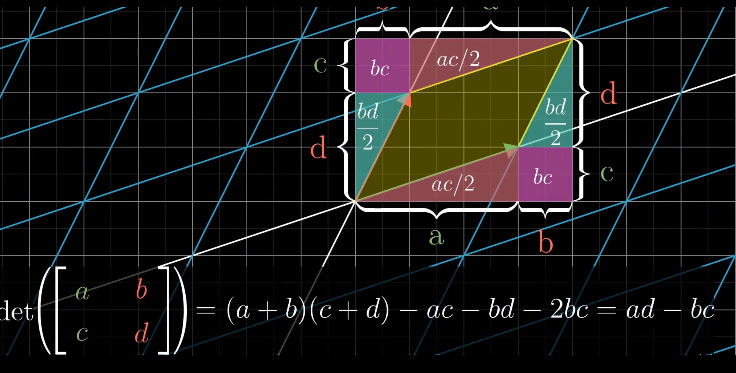
于是就有了两种计算\(\mathbb R^2\)行列式的办法
$$det(A)=|A||B|sin\theta$$
这个平行四边形同时适用于Cross Product于Determinate
这一个公式同样也是[[Cross Product 向量叉乘]]的大小(Norm),同时也是一个3x3Determinate的大小(体积)
如果说Cross Product要找的是一个向量,Determinate要找的则是一个体积
总的来说,要找\(R^2\)中的Determinate的值,其本质在求Linear Transformation后Basis Vector围成的面积
而这一个面积可以通过\(|A||B|sin\theta\)求,其同时也可以通过
两个向量的Position Vector上的点的差值求
其最后化简之后便有
$$\text{det} \left( \begin{bmatrix} a & b \ c & d \end{bmatrix} \right)
= (a + b)(c + d) - ac - bd - 2bc = ad - bc
$$
这便是Determinate最初的定义
The Determinate of a 3x3 Matrix
#
$$A = \begin{bmatrix}
a_{11} & a_{12} & a_{13} \
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33}
\end{bmatrix}
= \begin{bmatrix}
| & | & | \
\vec{u} & \vec{v} & \vec{w} \
| & | & |
\end{bmatrix}
$$
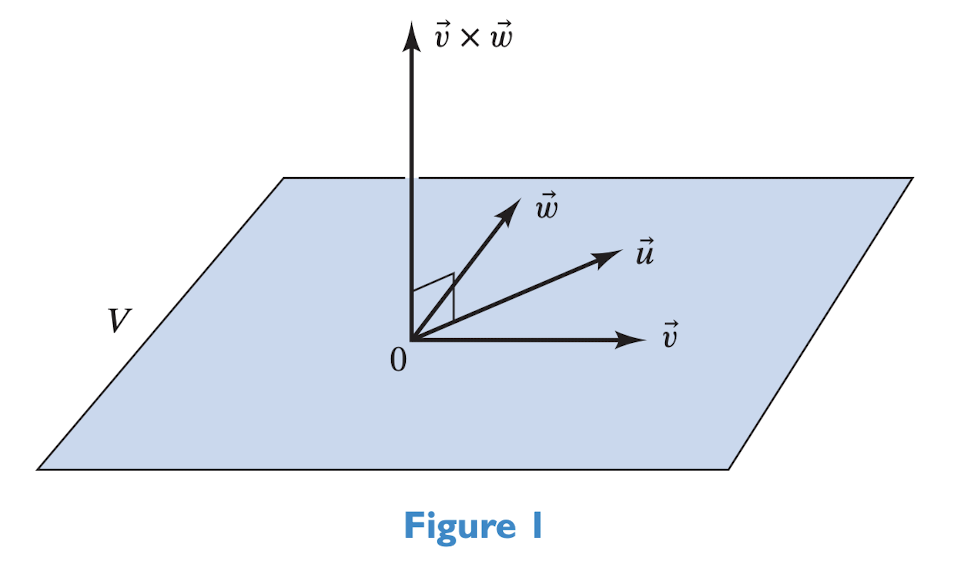
3x3的Matrix的Determinate的几何意义为在\(\mathbb R^3\)中的Parallelepiped的Volume
而对于\(\mathbb R^3\)中的三个向量来说,如果它们线性相关(如共面,即两个向量可以通过Lienar Conbination得到第三个向量的情况下),则他们在3x3Determinate的几何意义也是就是体积便不再存在,其是一个高度为0的长方体
具体来说判断的方法便是\(\vec{u} \cdot (\vec{v} \times \vec{w}) = 0\),见下图
Determinate为0的几何意义
#
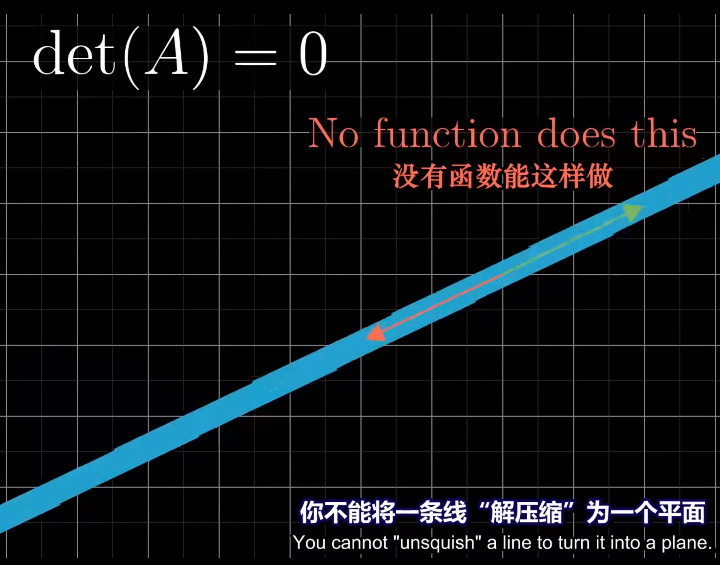
具体来说,当\(det(A)=0\)的时候,其相当于一个Linear Transformation至少压缩了一个维度
而在维度被压缩之后,此过程并不可逆,见下图
Definition 6.1.1 Determinant of a 3 × 3 matrix, in terms of the Columns
#
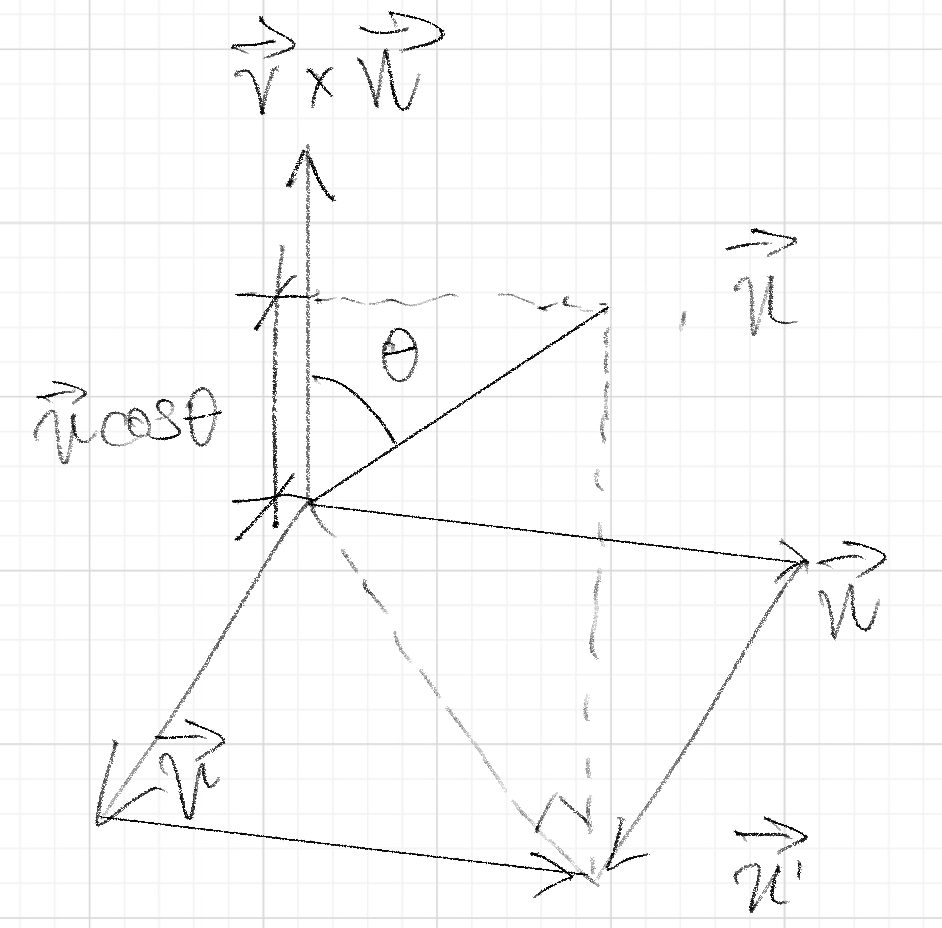
在上面提到过了行列式的几何意义为体积,而\(\vec u,\vec v\)并不会一直出现在xy Plane中,要计算其体积,基本上要用底面积乘以高的形式
而底面积则可以通过\(\vec c= \vec v\times \vec w\)的Cross Product,同时求出其大小与方向
具体来说,其大小即为\(|u|\),而其方向应该是垂直于vw Plane的
而将\(\vec u\cdot \vec c\)时,则可以得到Determinate中的第三个Vetor在一个垂直于vw Plane的同时具有方向和大小的向量\(\vec c\)上的Projection长度乘以其向量\(\vec c\)(本身Norm为vw所围成的平行四边形的面积)
则最终得到Determinate中的第三个向量\(\vec u\)在一个垂直于vw Plane的方向上的分量,在几何意义上来说为平行六面体的高
和一个\(\vec v\times \vec w\)所得到的两个向量围成的平行四边形的长度,即平行六面体的底面积
两者相乘便可以得到该3x3 Matrix Determinate的值,即这三个Vector所围成的Parallelepiped体积\
$$\begin{align}\text{det} , A = \vec{u} \cdot (\vec{v} \times \vec{w}) \
= \begin{bmatrix} a_{11} \ a_{21} \ a_{31} \end{bmatrix}
\cdot \left( \begin{bmatrix} a_{12} \ a_{22} \ a_{32} \end{bmatrix}
\times \begin{bmatrix} a_{13} \ a_{23} \ a_{33} \end{bmatrix} \right) \
= \begin{bmatrix} a_{11} \ a_{21} \ a_{31} \end{bmatrix}
\cdot \begin{bmatrix} a_{22}a_{33} - a_{32}a_{23} \ a_{32}a_{13} - a_{12}a_{33} \ a_{12}a_{23} - a_{22}a_{13} \end{bmatrix} \
= a_{11}(a_{22}a_{33} - a_{32}a_{23}) + a_{21}(a_{32}a_{13} - a_{12}a_{33}) + a_{31}(a_{12}a_{23} - a_{22}a_{13}) \
= a_{11}a_{22}a_{33} - a_{11}a_{32}a_{23} + a_{21}a_{32}a_{13} - a_{21}a_{12}a_{33} + a_{31}a_{12}a_{23} - a_{31}a_{22}a_{13}\end{align}
$$
上述介绍的所有都是有助于理解Determinant的而非考试的重点,意义在于理解,正式的内容将从下面开始
Properties of Determinant
#
Linearity of Determinant
#
行列式对任何一列或一行都是线性的
也就是说,当我们把一列(或一行)表示为两个向量的和或乘以一个标量时,行列式也可以相应地拆分为两个行列式的和,或乘以标量
当有如下Determinate时
$$L(\vec{x}) = \text{det} \left(
\begin{bmatrix}
- & \vec{v}_1 & - \\
- & \vec{v}_2 & - \\
- & \vec{x}+\vec y & -
\end{bmatrix}
\right)$$
- Matrix23位置的值为一个Variable x,而因为det在任意一行,列中都是线性的,即其也满足Linear的两个定义
$$L(\vec{x} + \vec{y}) = L(\vec{x}) + L(\vec{y}) \quad \text{and} \quad L(k\vec{x}) = kL(\vec{x})$$
- 在Determinate中有
$$\text{det} \left(
\begin{bmatrix}
- & \vec{v}_1 & - \\
- & \vec{v}_2 & - \\
- & \vec{x} + \vec{y} &-
\end{bmatrix}
\right)
= \text{det} \left(
\begin{bmatrix}
- & \vec{v}_1 & - \\
- & \vec{v}_2 & - \\
- & \vec{x} & -
\end{bmatrix}
\right)
+ \text{det} \left(
\begin{bmatrix}
- & \vec{v}_1 & - \\
- & \vec{v}_2 & - \\
- & \vec{y} & -
\end{bmatrix}
\right)
$$
$$\text{det} \left(
\begin{bmatrix}
- & \vec{v}_1 & - \\
- & \vec{v}_2 & - \\
- & k\vec{x} & -
\end{bmatrix}
\right)
= k \, \text{det} \left(
\begin{bmatrix}
- & \vec{v}_1 & - \\
- & \vec{v}_2 & - \\
- & \vec{x} & -
\end{bmatrix}
\right)
$$
- 如果在矩阵的一行乘上 t而剩下的n-1行保持不变,则行列式的值就要乘上 t
$$\left| \begin{array}{cc}
ta & tb \\
c & d
\end{array} \right|
= t
\left| \begin{array}{cc}
a & b \\
c & d
\end{array} \right|
$$
- 同理对于Linear Transformation的另外一个性质也通用
$$\left| \begin{array}{cc}
a + a' & b + b' \\
c & d
\end{array} \right|
=
\left| \begin{array}{cc}
a & b \\
c & d
\end{array} \right|
+
\left| \begin{array}{cc}
a' & b' \\
c & d
\end{array} \right|
$$
- 需要知道的是,这并不是在说$$det(A+B)=det(A)+det(B)$$
- 而是对于Square Matrxi的每一行来说是Linear的
Change of matrix’s effect on Determinate
#
当交换矩阵的两行,Determinant的值将会变号
如果你交换一个3×3矩阵的两行,行列式的值也会反号
同理也能知道
$$\left| \begin{array}{cc}
0 & 1 \\
1 & 0
\end{array} \right|
= -1
$$
Non-Squre Matrix Can’t Have Determinate
#
Non-Squre的Matrix会出现在当有两行是完全相同的时候
其证明可以是,当交换了两个相同的Matrix的Row的时候,其根据[[#Change of matrix’s effect on Determinate]]会发生变号,而可以观察发现新的Matrix和原来的没有区别,有Det=-Det,所以det=0
Row Operation’s influence on Determinate
#
从矩阵的某行 k 减去另一行 i 的倍数,并不改变行列式的数值(消元的过程不改变行列式)
$$\left| \begin{array}{cc}
a & b \\
c - ta & d - tb
\end{array} \right|
=
\left| \begin{array}{cc}
a & b \\
c & d
\end{array} \right|
-
\left| \begin{array}{cc}
a & b \\
ta & tb
\end{array} \right|
$$
$$=
\left| \begin{array}{cc}
a & b \\
c & d
\end{array} \right|
- t
\left| \begin{array}{cc}
a & b \\
a & b
\end{array} \right|
$$
- 根据[[#Change of matrix's effect on Determinate]],后一项的Determinant为0,即整体Det不变
Zero Rows Determinant
#
矩阵 A 的某一行都是 0,则其行列式为 0
根据[[#Linearity of Determinate]]可以知道,当t=0的时候,
$$\left| \begin{array}{cc}
ta & tb \\
c & d
\end{array} \right|
= t
\left| \begin{array}{cc}
a & b \\
c & d
\end{array} \right|$$
- 有$$\left| \begin{array}{cc}
0\cdot a & 0\cdot b \\
c & d
\end{array} \right|= 0
\left| \begin{array}{cc}
a & b \\
c & d
\end{array} \right|$$
Trangular Matrix’s Determinant
#
$$\left| \begin{array}{cccc}
d_1 & * & \cdots & * \\
0 & d_2 & \cdots & * \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & d_n
\end{array} \right|
=
\left| \begin{array}{cccc}
d_1 & 0 & \cdots & 0 \\
0 & d_2 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & d_n
\end{array} \right|
= d_1 d_2 \cdots d_n
\left| \begin{array}{cccc}
1 & 0 & \cdots & 0 \\
0 & 1 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 1
\end{array} \right|
= d_1 d_2 \cdots d_n
$$
根据[[#Row Operation’s influence on Determinate]],当是通过Row Operation得到Triangular Matrix的时候,正负号可能发生改变
对于非Diagonal上的元素,根据[[#Row Operation’s influence on Determinate]]可以做Row Operation在不改变Determinant的前提下将他们全部消掉,有
$$\left| \begin{array}{cccc}
d_1 & * & \cdots & * \\
0 & d_2 & \cdots & * \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & d_n
\end{array} \right|= \left| \begin{array}{cccc}
d_1 & 0 & \cdots & 0 \\
0 & d_2 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & d_n
\end{array} \right|$$
- 再通过[[#Linearity of Determinate]]提取出每个Row Pivot上的d
$$= d_1 d_2 \cdots d_n
\left| \begin{array}{cccc}
1 & 0 & \cdots & 0 \\
0 & 1 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 1
\end{array} \right|
= d_1 d_2 \cdots d_n$$
Singular Matrix’s Determinant
#
对于Rank小于Row的Square Matrix,其Determinant为0
Numerial Approach of Determinant
#
当有一个Matrix的时候,想要计算其Determinant,即需要将其化为Triangular Matrix,最简单的方式即为化为Upper Triangular Matrix
而要消成Upper Triangular Matrix的方式即为将C化为0(拿2x2Matrix举例)
$$\left[ \begin{array}{cc}
a & b \\
c & d
\end{array} \right]
\rightarrow
\left[ \begin{array}{cc}
a & b \\
0 & d - \frac{c}{a}b
\end{array} \right]
$$
$$\left| \begin{array}{cc}
a & b \
c & d
\end{array} \right|
= a \left( d - \frac{c}{a}b \right) = ad - bc
$$
Determinant of Product
#
\(det(AB)=det(A)\cdot det(B)\)
\(det(A+B)\neq det(A)+det(B)\)
Determinant of Inverse
#
\(det(A^{-1})\)
已知\(A^{-1}A=I\),即\(det(A^{-1})det(A)=det(I)=1\)
则有\(det(A^{-1})=\frac{1}{det(A)}\)
Determinant of Square
#
\(det(A^2)=det(A)^2=det(A)\cdot det(A)\)
Determinant of Coefficient before Matrix
#
\(det(2A)=2^ndet(A)\)
对于nxn Matrix来说,犹豫每一个Row都乘上的Coefficient 2,即存在\(2^n\)的总系数
Determinant of Transpose
#
$$\left| \begin{array}{cc}
a & b \\
c & d
\end{array} \right|
=
\left| \begin{array}{cc}
a & c \\
b & d
\end{array} \right|
= ad - bc
$$
Formular for Determinant
#
2x2
#
$$\left| \begin{array}{cc}
a & b \\
c & d
\end{array} \right|
=
\left| \begin{array}{cc}
a & 0 \\
c & d
\end{array} \right|
+
\left| \begin{array}{cc}
0 & b \\
c & d
\end{array} \right|
=
\left| \begin{array}{cc}
a & 0 \\
c & 0
\end{array} \right|
+
\left| \begin{array}{cc}
0 & d \\
0 & d
\end{array} \right|
+
\left| \begin{array}{cc}
0 & b \\
0 & d
\end{array} \right|
=
0 + ad - cb + 0
=
ad - bc
$$
3x3
#
将每一行拆成3部分,每一部分都对应了不同的行上的不同元素
总共会得到\(3^3\)个Matrix即27个,而其中大部分Matrix由于行或列上全为0有Det=0
而其中的非零情况出现在每一列都有的情况下(因为我们是从行出发开始分解的,所以每一行都保证了有值)
$$\left| \begin{array}{ccc}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array} \right|
=
\left| \begin{array}{ccc}
a_{11} & 0 & 0 \\
0 & a_{22} & 0 \\
0 & 0 & a_{33}
\end{array} \right|
+
\left| \begin{array}{ccc}
a_{11} & 0 & 0 \\
0 & 0 & a_{23} \\
0 & a_{32} & 0
\end{array} \right|
+
\left| \begin{array}{ccc}
0 & a_{12} & 0 \\
a_{21} & 0 & 0 \\
0 & 0 & a_{33}
\end{array} \right|
+
\left| \begin{array}{ccc}
0 & a_{12} & 0 \\
0 & a_{22} & 0 \\
a_{31} & 0 & 0
\end{array} \right|
+
\left| \begin{array}{ccc}
0 & 0 & a_{13} \\
a_{21} & 0 & 0 \\
0 & a_{32} & 0
\end{array} \right|
+
\left| \begin{array}{ccc}
0 & 0 & a_{13} \\
0 & a_{22} & 0 \\
a_{31} & 0 & 0
\end{array} \right|
$$
$$=
a_{11}a_{22}a_{33} - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33}
+ a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31}$$
- 其中所有的负值,都是用了[[#Change of matrix's effect on Determinate]]将Matrix做Row Exchange成Uppertriangular Matrix而导致的Determinant的变号
但这个做法再4x4中并不通用,所以需要从2x2,3x3中推导出nxn的公式
Big Formula A
#
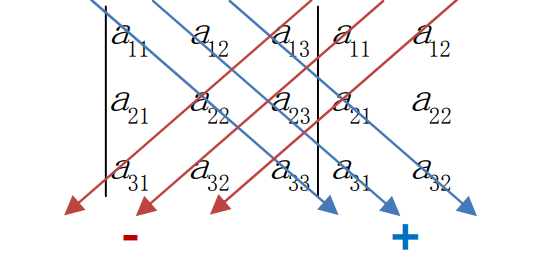
$$det(A)=\sum_{n!}\pm a_{1\alpha}a_{2\beta}a_{3\gamma}\dots a_{n\omega}$$
\(n!\):由于我们是用Row做的,即在Row1中有n个Column可以选,而到了Row2中,只有n-1个Column可以选,以此类推可能性即为\(n!\)
\(\alpha,\beta,\gamma,\omega\):列标号中的任何值
$$\left| \begin{array}{cccc}
0 & 0 & 1 & 1 \\
0 & 1 & 1 & 0 \\
1 & 1 & 0 & 0 \\
1 & 0 & 0 & 1
\end{array} \right|
=
\left| \begin{array}{cccc}
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
1 & 0 & 0 & 0
\end{array} \right|
+
\left| \begin{array}{cccc}
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1
\end{array} \right|
$$
分解出的两个Matrix中,第一个需要做两次Row Exchange得到Identity,即为1,而第二个则需要1次Row Exchange就可以得到Identify,即为-1,1-1=0
Cofactor Formula 代数余子式
#
3x3
#
代数余子式是用较小的矩阵的行列式来写出 n 阶行列式的公式
$$\text{det} \left( \mathbf{A} \right) = a_{11} \left( a_{22}a_{33} - a_{23}a_{32} \right)
+ a_{12} \left( -a_{21}a_{33} + a_{23}a_{31} \right)
+ a_{13} \left( a_{21}a_{32} - a_{22}a_{31} \right)
$$
$$=\left| \begin{array}{ccc}
a_{11} & 0 & 0 \\
0 & a_{22} & a_{23} \\
0 & a_{32} & a_{33}
\end{array} \right|
+
\left| \begin{array}{ccc}
0 & a_{12} & 0 \\
a_{21} & 0 & a_{23} \\
a_{31} & 0 & a_{33}
\end{array} \right|
+
\left| \begin{array}{ccc}
0 & 0 & a_{13} \\
a_{21} & a_{22} & 0 \\
a_{31} & a_{32} & 0
\end{array} \right|$$
由于第二个Martri在化为Identity时只需要一次Row Exchange而其他的都需要两次,所以第二个Cofactor为减去
Cofactor Formula
#
将原公式中属于矩阵第一行的\(a_{ij}\)提出来,其系数即为代数余子式,是一个低阶行列式的值。这个低阶行列式是由原矩阵去掉\(a_{ij}\)所在的行和列组成的。
对矩阵中任意元素\(a_{ij}\)而言,其代数余子式\(C_{ij}\)j就是矩阵的行列式的公式中\(a_{ij}\)的系数
\(C_{ij}\)等于原矩阵移除第i行和第j列后剩余元素组成的n-1阶矩阵的行列式数值乘以\((-1)^{i+j}\)
\(C_{ij}\)在 i+j 为偶数时为正,奇数时为负数
则可以总结对于n阶Square Matrix来说,有
$$\text{det} \left( \mathbf{A} \right) = a_{11} C_{11} + a_{12} C_{12} + \cdots + a_{1n} C_{1n}
$$
ex. in 2x2
#
Cofactor Formula最简单的应用即为在2x2 Matrix中,有
$$\left| \begin{array}{cc}
a & b \\
c & d
\end{array} \right|
= ad + b(-c)$$
ex. 三对角阵(tridiagonal matrix)
#
只在Tridiagonal Matrix这种特殊结构中可行
$$\mathbf{A_4} = \left[ \begin{array}{cccc}
1 & 1 & 0 & 0 \\
1 & 1 & 1 & 0 \\
0 & 1 & 1 & 1 \\
0 & 0 & 1 & 1
\end{array} \right]
$$
![[LA6.Determinats-9.png]]
Formula for A Inverse
#
$$\left[ \begin{array}{cc}
a & b \\
c & d
\end{array} \right]
= \frac{1}{ad - bc}
\left[ \begin{array}{cc}
d & -b \\
-c & a
\end{array} \right]
$$
- 通过观察上2x2的例子可以得出
$$\mathbf{A}^{-1} = \frac{1}{\det(\mathbf{A})} \mathbf{C}^\top$$
通过观察可以发现d是a的C,-b是c的C,-c是b的C,a是d的C
Adjoint Matrix 伴随矩阵
#
此处的Cofactor的Transpose\(C^T\)便可以称为Adjoint Martirx,即伴随矩阵
对于Adjoint Matrix来说,其大小总是原Matrix的Dimension-1即为n-1
Proof of A Inverse
#
已知Gauss Jordan Elimination提到\([A|I]\)在A被消成I后,I会变成\(A^{-1}\)
同时\(A^{-1}A=I\),现在将\(\mathbf{A}^{-1} = \frac{1}{\det(\mathbf{A})} \mathbf{C}^\top\)带入
$$A\cdot \mathbf{A}^{-1} = A\cdot\frac{1}{\det(\mathbf{A})} \mathbf{C}^\top=I$$
$$A\cdot C^T=det(A)\cdot I$$
如果上式成立,则\(\mathbf{A}^{-1} = \frac{1}{\det(\mathbf{A})} \mathbf{C}^\top\)为真命题
$$\mathbf{AC}^T = \begin{bmatrix}
a_{11} & \cdots & a_{1n} \\
\vdots & \ddots & \vdots \\
a_{n1} & \cdots & a_{nn}
\end{bmatrix}
\begin{bmatrix}
C_{11} & \cdots & C_{n1} \\
\vdots & \ddots & \vdots \\
C_{1n} & \cdots & C_{nn}
\end{bmatrix}
$$
- 对于所有结果矩阵对角线上的的元素来说都有
$$\sum_{j=1}^{n} a_{1j} C_{1j} = \det(\mathbf{A})$$
即他们本身就是det(A)的展开式
而现在要研究结果矩阵非对角线上的内容
$$AC^T = \begin{bmatrix}
\det A & 0 & 0 & \cdots & 0 \\
0 & \det A & 0 & \cdots & 0 \\
0 & 0 & \ddots & \cdots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \cdots & \det A
\end{bmatrix} = \det(A)I
$$
Cramer’s Rule 克莱姆法则
#
对于问题Ax=b来说,其解法很简单的就等于\(x=A^{-1}B\)
而在知道了\(A^{-1}\)的值之后有
$$\mathbf{x} = \mathbf{A}^{-1} \mathbf{b} = \frac{1}{\det(\mathbf{A})} \mathbf{C}^T \mathbf{b}$$
选择乘上\(C^T\) 的不再是A而是b了,但一个Matrix乘以一个Cofactor Matrix的做法又令人想到了Determinant,可以发现
$$x_j = \frac{\det(\mathbf{B}_j)}{\det(\mathbf{A})}
$$
其中每一个\(B_i\)都是一个第i列被\(B_i\)所替换的Matrix A,具体来说有
$$\mathbf{B}_1 = \begin{bmatrix}
b_1 & a_{12} & \cdots & a_{1n} \\
b_2 & a_{22} & \cdots & a_{2n} \\
b_3 & a_{32} & \ddots & \vdots \\
\vdots & \vdots & \ddots & a_{n-1\,n} \\
b_n & a_{n2} & \cdots & a_{nn}
\end{bmatrix}
, \quad
\mathbf{B}_n = \begin{bmatrix}
a_{11} & \cdots & a_{1\,n-1} & b_1 \\
a_{21} & \cdots & a_{2\,n-1} & b_2 \\
\vdots & \ddots & \vdots & \vdots \\
a_{n-1\,1} & \cdots & a_{n-1\,n-1} & b_{n-1} \\
a_{n1} & \cdots & a_{n2} & b_n
\end{bmatrix}
$$
可以发现等式中的\(C^T_i \cdot B_i\)正好等于\(B_i\)的Determinant
其实相比于消元法,采用克莱姆法则计算方程的解效率较低。。。