DYN 1. Rectilinear Motion Edited
Last Edit: 3/24/25
直线运动指的是物体沿着一条直线路径移动。这种运动的特点是,物体的速度和加速度(如果有的话)的方向只在一条直线上
Velocity & Speed #
- Velocity,瞬时速度,\(\vec v=\frac{d\vec s}{dt}\)
- Average Velocity,一个区间内的平均速度 \(\vec{v}_{avg}=\frac{\Delta \vec x}{\Delta t}\)
- Speed,Scalar,\(|\vec v|\)
Acceleration 加速度 #
- 加速度是 Velocity 的 Second Derivative
$$ a=\frac{d\vec v}{dt}=\frac{d^2\vec x}{dt^2} $$
Acceleration as a function of time a(t) #
- 当 Acceleration 是时间t的函数的时候(也就是说加速度在随着事件 t 变化而变化时),这种情况下,例如一个汽车加速或减速,有s和v等于
$$ a(t) = \frac{dv}{dt} \implies \int_{t_0}^{t} a(t) , dt = \int_{v_0}^{v} dv = v - v_0 \implies v = v_0 + \int_{t_0}^{t} a(t) , dt $$
$$ v(t) = \frac{ds}{dt} \implies \int_{t_0}^{t} v , dt = \int_{s_0}^{s} ds = s - s_0 \implies s = s_0 + \int_{t_0}^{t} \left[ v_0 + \int_{t_0}^{t} a(t) , dt \right] dt $$
- 对于上面的公式,当加速度a是一个Constant的时候
$$ v=v_0+\int_{t_0}^{t} a , dt=v_0+a\int_{t_0}^{t} , dt=v_0+a(t-t_0) $$
- 同理s也就有
$$ s=s_0+\int_{t_0}^{t} \left[ v_0+a(t-t_0) \right] dt=s_0+\frac{1}{2}at^2-at_0t+v_0t $$
Acceleration is a function of position a(s) #
- 在这种情况下,加速度取决于位置,这常见于诸如重力势能场中物体的运动
- 同理Acceleration是速度对于时间的导数,有
$$ a(s)=\frac{dv}{dt}\Rightarrow dt=\frac{dv}{a(s)} $$
- 又因为 Velocity 是 Speed 对于时间的导数,有
$$ v=\frac{ds}{dt}\Rightarrow dt=\frac{ds}{v} $$
- 建立等式便可得到
$$ \frac{dv}{a(s)}=\frac{ds}{v}\Rightarrow \int a(s)ds=\int vdv=\frac{1}{2}(v^2-{v_0}^2) $$
- 同理当a是Constant的时候有
$$ \frac{1}{2}(v^2-{v_0}^2)=a\int^s_{s_0}ds=a\Delta S\Rightarrow v^2={v_0}^2+2a\Delta S $$
在加速度是位置的函数的时候没有对于s的公式
ex. Speed of asteroid falling #
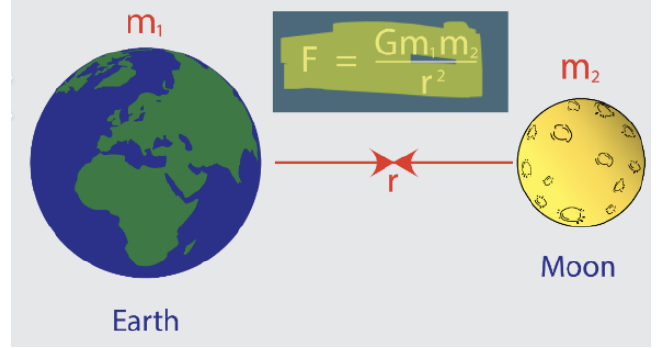
Find the impact speed of an asteroid falling to earth from a height of 109m (from the center of earth), when 𝑣𝑜 =-50 m/s. Consider m(earth)=6e24 kg, and G=6.67e-11Nm²/kg², and r(earth)=6.4e6 m
- 已知u,S0,Sf,求Vf,已知加速度是Position s的函数 \(a=\frac{Gm_e}{r^2}\)
$$ v^2={v_0}^2-2\int\frac{Gm_e}{s^2}ds={v_0}^2+2Gm_e(\frac{1}{s}-\frac{1}{s_0}) $$
Acceleration as a function of velocity a(v) #
- 加速度为速度 v 的函数
$$ a(v)=\frac{dv}{dt}\Rightarrow dt=\frac{dv}{a(v)}\Rightarrow \int^t_{t_0}dt=\int^v_{v_0}\frac{dv}{a(v)}=t-t_0 $$
ex. Projectile Motion #
A projectile travels through fluid with an initial velocity of 60 m/s. The acceleration is 𝑎 = −0.4 v3𝑚/𝑠². Find v after 4 s
- 可以发现a是v的函数,有 \(a(v)=-0.4v^3\)
$$ a(v)=\frac{dv}{dt}\Rightarrow \int^t_{t_0} dt=\int\frac{dv}{-0.4v^3}=\frac{-1}{0.4}\int v^{-3}dv $$
- 分别求出积分后得到
$$ t-t_0=\frac{-1}{0.4}\frac{-1}{2}=(\frac{1}{v^2}-\frac{1}{{v_0}^2})\Rightarrow v=0.559m/s $$
Summary #
- 加速度 a(t) 是时间的函数
$$ ∫dv=∫a(t) dt\int dv = \int a(t) , dt $$
- 加速度 a(s) 是位移的函数
$$ ∫v dv=∫a ds\int v , dv = \int a , ds $$
- 加速度 a(v) 是速度的函数
$$ ∫dva(v)=∫dt\int \frac{dv}{a(v)} = \int dt $$
- 当a是常数的时候
$$ V = V_0 + at $$
$$ S = S_0 + V_0 t + \frac{1}{2} a t^2 $$
$$ V^2 = V_0^2 + 2a \Delta s $$