Last Edit: 11/19/24
Solution 解 #
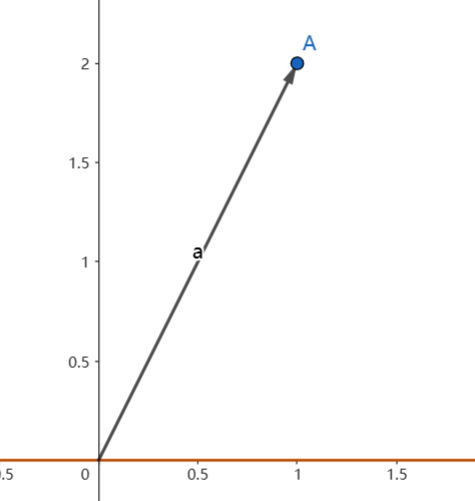
- 对于一个Vector \(a=[1,2]^T\)和一个直线\(y=0\)
- 要研究\(c[1,2]^T=0\)的问题的时候,很明显不存在Non-Trivial Solution
- 由于a在\(R^2\)中,而\([1,0]^T\)仅Span出了\(R^2\)中的一个Subspace,其Dim=1
Least Error Solution (Optimization) 最优解 #
- 但是对于a到直线的距离仍存在Optimized Solution
- 最优解出现在\([1,2]^T\)的终点在\([1,0]\)方向上最短的情况,即一个Error最小的情况
- 可以从a出发找到无数个到达向量\([1,0]^T\)方向的向量
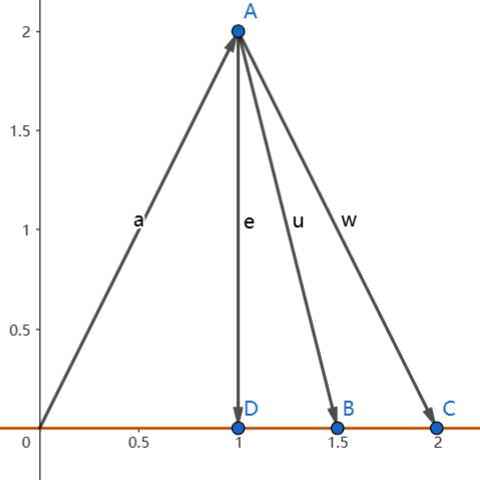
- 而其中最短的则是\(\vec {e}\)
- 也可以说\(\vec e\)是Equation Error最小的Solution
R^3 Case #
- 对于向量\([1,1,3]^T\)来说,要计算其到达平面\(x+y-2z=0\)的最短距离
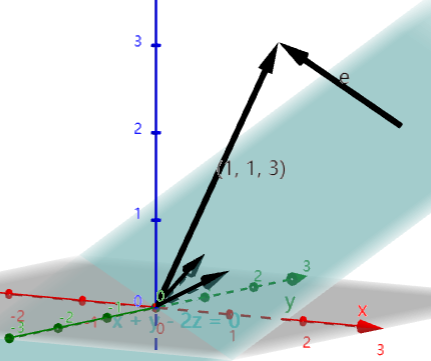
- \(\vec e\) 则代表了这一个距离
- 则e的起点在Plane\(x+y-2z=0\)上的位置就是这一个最优解
Projection 投影 #
- 可以发现,要找到最优解,一个合理的办法是从Projection开始
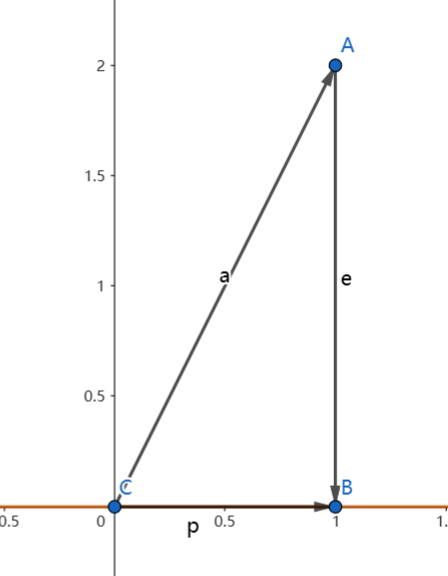
- 在上图中p就是a在\([1,0]^T\)方向上的投影
- 则有\(e=b-p\)
- 而最小化这个e就是目标,这个目标通过Orthogonal 正交实现
- 具体来说从A出发的orthogonal to p的vector e就是这个Optimized Solution
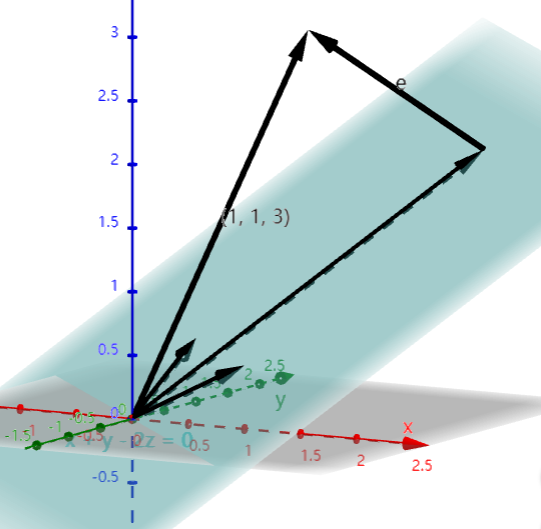
- \(R^3\)中同理,只不过是将投影的改为了Plane
- 于是便有\(e=(b-A\hat x)\)
- 要让e垂直于Plane \(A=[a1,a2]\)
- 有\(a_1^T(b-A\hat x )=0\)并且\(a_2^T(b-A\hat x )=0\)
- 于是可以得到公式 $$A^T(b-A\hat x)=0\Rightarrow A^TA\hat x=A^Tb$$
Least Squares 最小二乘 #
- 直接进入例子

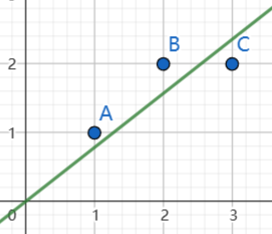
- 对于三个点{(1,1), (2,2), (3,2)}
- 构建方程\(y=wx\)
- 带入点后得到\(1=w,2=2w,2=3w\)
- 通过\(A^TA\hat x=A^Tb\)
$$A^T A = \begin{bmatrix}
1 & 2 & 3
\end{bmatrix}
\begin{bmatrix}
1 \\
2 \\
3
\end{bmatrix}
= 1^2 + 2^2 + 3^2
= 1 + 4 + 9
= 14$$
$$A^T b = \begin{bmatrix}
1 & 2 & 3
\end{bmatrix}
\begin{bmatrix}
1 \\
2 \\
2
\end{bmatrix}
= 1 \cdot 1 + 2 \cdot 2 + 3 \cdot 2
= 1 + 4 + 6
= 11
$$
- 便有\(14w=11\Rightarrow w=\frac{11}{14}\)
几何角度 #
- 那么上面的公式在几何空间中干的事就是
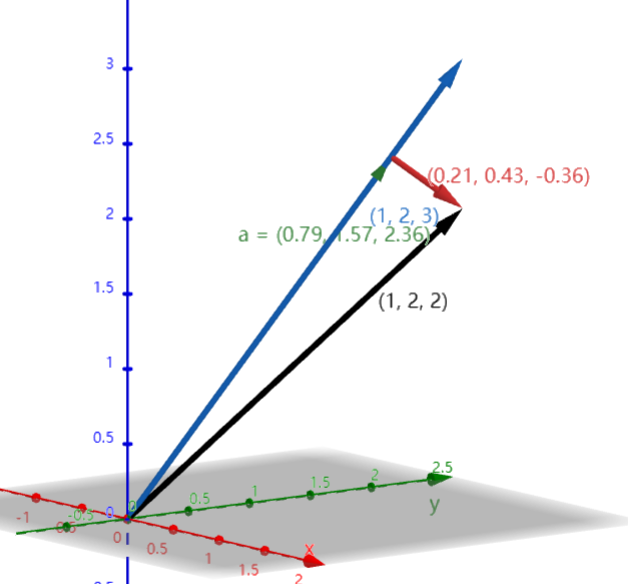
- 找到了这个红色的Vector,也就是最小的e
- 同理运用到最经典的\(y=wx+b\)也是一样
- \(1=w+b,2=2w+b,2=3w+b\)
$$A^T A = \begin{bmatrix} 1 & 2 & 3 \\ 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} 1 & 1 \\ 2 & 1 \\ 3 & 1 \end{bmatrix} = \begin{bmatrix} 1^2 + 2^2 + 3^2 & 1 + 2 + 3 \\ 1 + 2 + 3 & 3 \end{bmatrix} = \begin{bmatrix} 14 & 6 \\ 6 & 3 \end{bmatrix}$$
$$A^T \mathbf{b} = \begin{bmatrix} 1 & 2 & 3 \\ 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \\ 2 \end{bmatrix} = \begin{bmatrix} 1 \cdot 1 + 2 \cdot 2 + 3 \cdot 2 \\ 1 \cdot 1 + 1 \cdot 2 + 1 \cdot 2 \end{bmatrix} = \begin{bmatrix} 11 \\ 5 \end{bmatrix}$$
$$\begin{bmatrix} 14 & 6 \\ 6 & 3 \end{bmatrix} \begin{bmatrix} w \\ b \end{bmatrix} = \begin{bmatrix} 11 \\ 5 \end{bmatrix} $$
- 于是有\(w=\frac{1}{2},b=\frac{2}{3}\)
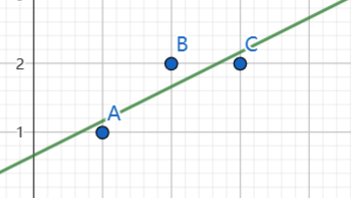
- 同理几何上找到了向量在Plane上的投影之间的最小Error
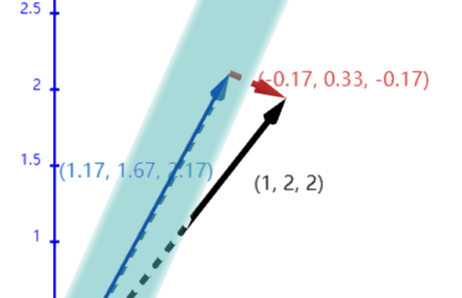
- 所以这就是\(A^TA\hat x=A^Tb\) 在Linear Regression的作用
- 需要知道的是这个方法(Normal Equation)求得的是解析解,在一般在feature < 10000的时候采用,但是过程可能不可逆