Last Edit: 11/25/24
The finger of time #
- 在上一章中讨论了Solide Crystalline Nacl的形成,我们知道它在室温和压力下是稳定的
- 同理当我们看到手机从人手上掉下来并不会感到惊讶
- 通过The Second Law Of Thermodynamics,我们可以意识到时间的流逝
The Second Law of Thermodynamics 热力学第二定律 #
- The entropy of the Universe increases during any spontaneous process
Spontaneous 自发的 #
- Spontaneous, here, means that the process proceeds on its own, without the need for an input of energy 代表了该过程自行进行,不需要能量输入
- 例如在空气中点燃一张纸,他将会燃烧,我面对如此现象并不会感到惊讶
Entropy 熵 #
- 前面反复的介绍的Second Law的重要性,而Entropy的存在将定义如何使用它
- 熵是一个衡量系统混乱程度的物理量,系统的熵越高,系统的无序程度就越高 $$\Delta S = \frac{q_{REV}}{T}$$
- S is the entropy 熵
- \(q_{rev}\) is the heat transferred 传递的热量
- T is the thermodynamic temperature 热力学温度,单位为Kelvin
The Thermodynamic Alphabet 热力学字母表 #
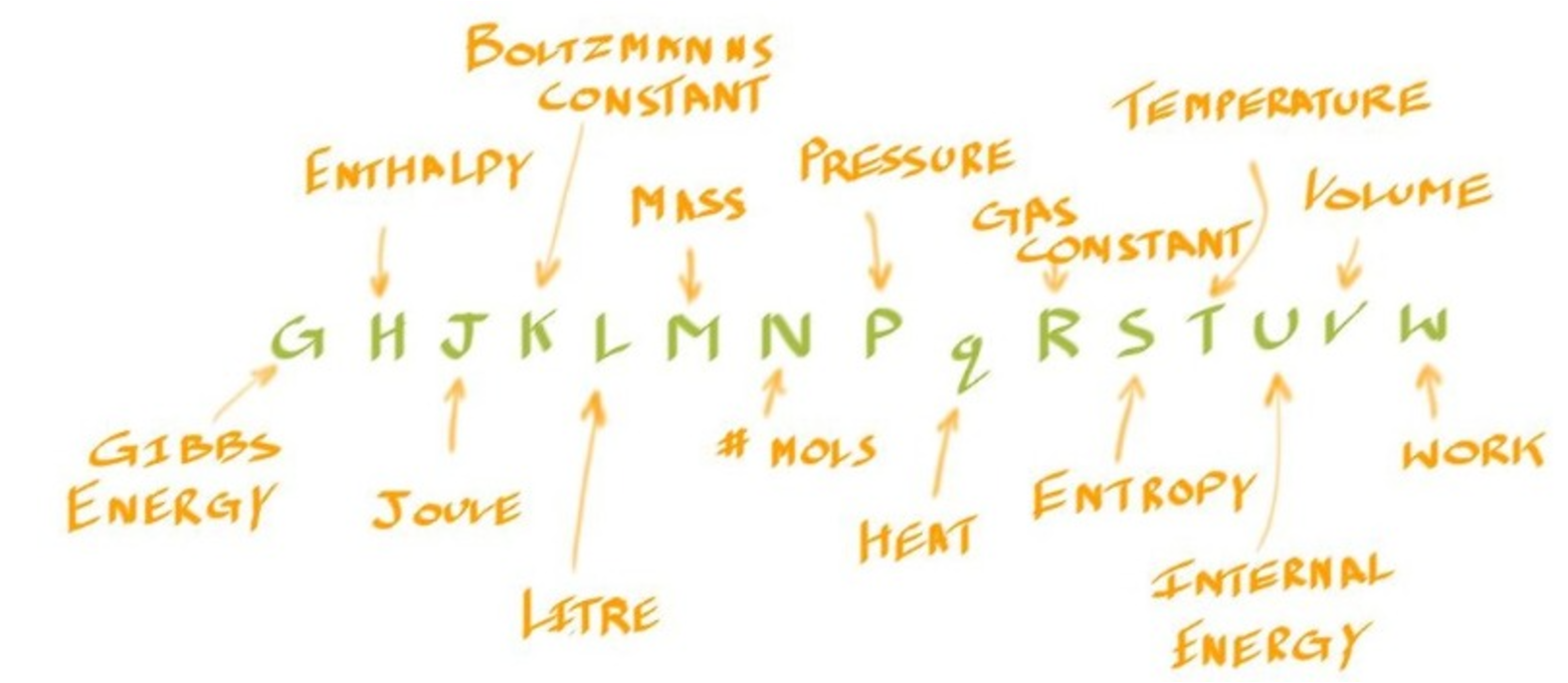
Reversibility 可逆性 #
- 对于rev的下标,这代表了Heat is transferred reversibly
- 但实际上Reversibility仅存在于Concept中,因为真实的物理过程总会有一些不可逆的因素,如摩擦,热损失等
System Surroundings and the Universe #
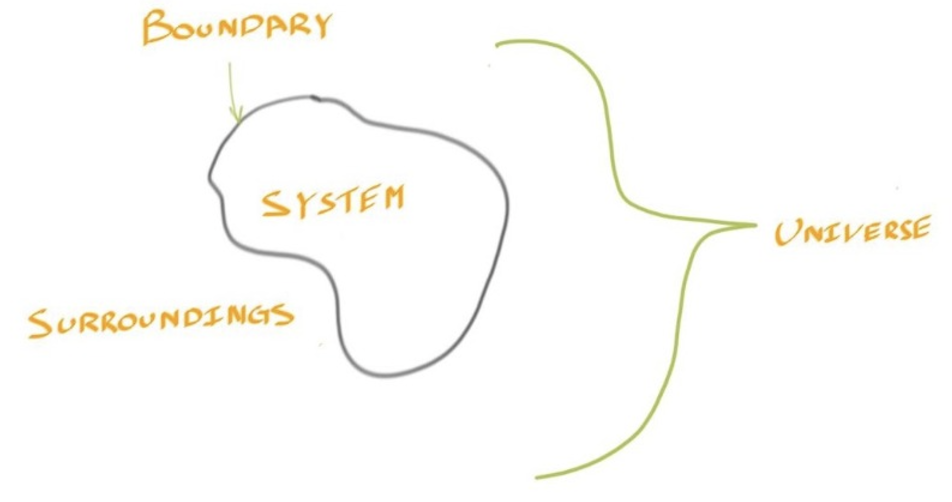
- 周围的一切都被叫做Surroundings
- 而System和Surrounding一起构成了Universe
- 带回到The Second law of thermodynamic中,有 $$\Delta S_{universe} = \Delta S_{system} + \Delta S_{surroundings} > 0$$
- 所以唯一的判断Spontaneous的要求即为当Entropy change for universe must be positive
The First Law of Thermodynamics 热力学第一定律 #
- 在一个孤立系统中,能量既不能被创造也不能被消灭,能量只能从一种形式转换为另一种形式,或者从一个物体传递到另一个物体 $$ΔU=q+w$$
Internal Energy 内能 #
- Internal Energy是一个System的总能量,包括所有可能的能量形式,如动能、势能、化学能等
- 在听到内能的时候,可能会联想到Fuel, battery or a Quantity of Nuclear Fuel,但他们都不是完全的
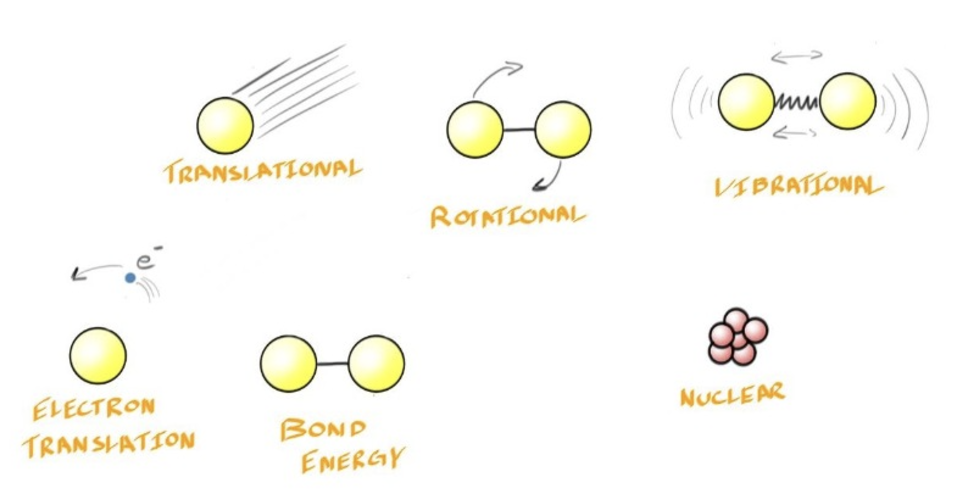
- 对于一个System其中存在着无数种能影响内能的能量形式,这也使得研究System的Internal Energy的Absolute Value变得难以测定以至于不具有实际意义
- 所以所研究的Internal Energy更多的是一种Change of Energy
- 而Change,是建立在所谓的控制变量法
Potential Energy - Water Bottle #
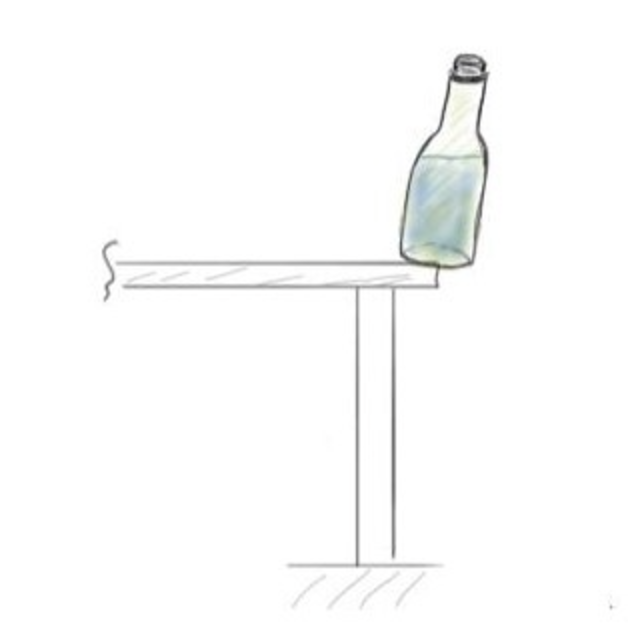
- 考虑上面的水平,要计算它的Internal Energy,我们会本能的选择一个Obvious Reference Surface从而计算瓶子相对于该平面的Potential Energy
- 同时,我们不需要考虑其动能或者是燃烧瓶子所释放的能量
- 这强调了在特定问题中选择关注特定类型能量的重要性
- Similarly, in thermodynamics we’ll need to define a logical reference point to measure changes in energy
Logical Reference Point - The Standard State #
- 在热力学和化学中,需要一个清晰、一致的基准来测量能量变化。比如,当讨论燃烧汽油(主要成分为辛烷)所需的能量时,我们需要一个基准状态作为起点
- 这段话在讨论热力学和化学中如何选择一个参考点,称为“Standard State”,来测量和比较化学反应和能量变化
- 标准状态是在特定条件下(通常是25°C和105帕斯卡压力),一种纯元素的最稳定形式
State Functions and Path Functions 状态和路径函数 #
- 再次考虑前面水瓶的例子 $$Water Bottle_{on table} → Water Bottle_{on high shelf}$$
State Function 状态函数 #
- It does not depend on how we got to the final state, all that matters is what that state is
- 它不取决于我们如何达到最终状态,重要的是那个状态是什么
- 另一个例子为Temperature,你不需要查阅过去的温度来计算现在的,只需要测量当前温度便可以, 这就是一种State Function
- 庆幸的是Internal Energy只能是一种State Function,这意味着内能的变化仅取决于系统的初始状态和最终状态。无论系统是通过何种过程从初始状态转变到最终状态,内能的变化总量是固定的
Path Function 路径函数 #
- 如果问题变成了,把水瓶从桌子上移到高架子上有多困难
- 做的工作取决 how you got there - it depends on the path
Closed Versus Isolated Systems 封闭系统与孤立系统 #
- 我们可以研究Boundaries开放且物质穿过它们的系统,但这不是我们现在需要考虑的
- 我们需要考虑systems where matter is not allowed to pass the boundaries的系统
Isolated System 隔离式系统 #
- No heat is exchanged with the surroundings $$ΔU=q+w,q=w=0\RightarrowΔU=0$$
Closed system 封闭系统 #
- Heat may pass the boundaries $$ΔU=q+w$$ - q is the heat transferring into the system
- w is the work done on the system
- Sign convention在这里很重要,heat in and work on are positive
Enthalpy 焓 #
- 焓(Enthalpy),符号为H,是热力学中的一个重要概念,用于描述系统在一定压力下的总热含量
- 焓是一个状态函数,它与系统的内能、压力和体积关系密切。焓的定义是 $$H=U+PV$$
- 其中U是内能,P是压力,V是体积
Enthalpy in Solid 固体中的焓 #
- 在固态物理过程中,物质的体积变化通常非常小,因此PV工作相对于内能U的变化可以忽略不计
- 所以在在固态物理领域,人们可能会将“Enthalpy”或“Enthalpy Change”与“Energy”或“Energy Change”这些术语互换使用
The Gibbs Energy 吉布斯自由能 #
$$G=H−TS$$
- G:吉布斯能量
- H:焓(系统的总能量,包括内能和体积功)
- T:温度(开尔文,K)
- S:熵(系统的无序程度)
- 这个定义说明吉布斯自由能考虑了系统的能量状态(Enthalpy)和无序度(Entropy)
Spontaneity for a system 系统的自发性 #
- 如果\(\Delta G < 0\):过程是自发的(有利于发生)。
- 如果\(\Delta G = 0\):系统达到平衡。
- 如果\(\Delta G > 0\):过程是非自发的(需要外界能量输入)
- 自发过程的基本条件是整个宇宙的熵(包括系统和环境的熵)总和需要增加,这是在前面的The Second Law of Thermodynamics中定义的 $$\Delta S_{\text{system}} + \Delta S_{\text{surroundings}} > 0$$
- 在恒温下,周围环境的熵变是进入周围环境的热量除以温度 $$\Delta S_{\text{Surroundings}} = \frac{q_{\text{Surroundings}}}{T}$$
- 离开系统的任何热量都与周围环境吸收的热量相同,或者相反,因此有 $$\Delta S_{\text{Surrounding}} = \frac{-q_{\text{System}}}{T}$$
- 于是就可以推出Spontaneous的同时由Entropy和Enthalpy定义的公式变为 $$\Delta H_{\text{system}}-T \Delta S_{\text{system}} < 0$$
Phase Transformations #
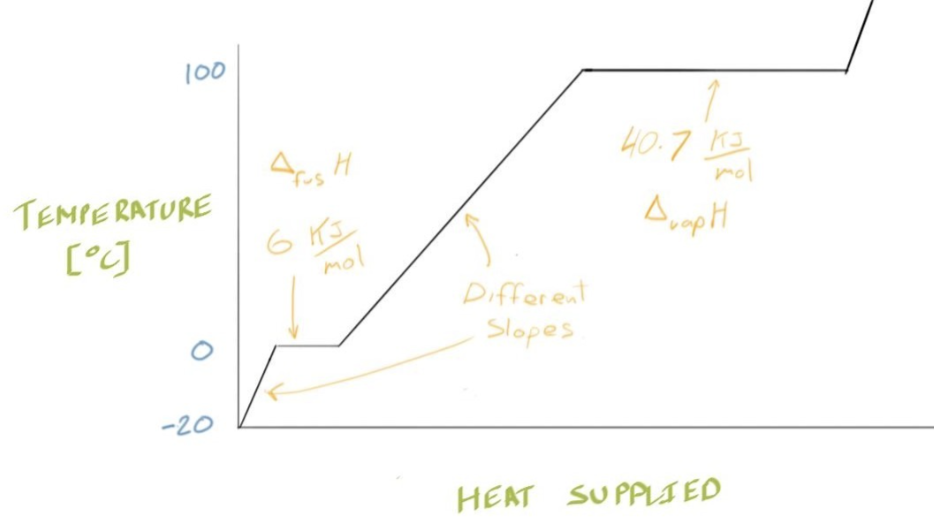
- 图中为对不同阶段的水加热后的变化
- 固态(冰)升温:在冰的温度低于 0°C 时,输入热量会使冰的温度上升。
- 熔化(0°C 平台):温度停止上升,因为输入的热量用于冰的相变(熔化),这个热量叫做熔化焓(enthalpy of fusion)。
- 液态(水)升温:冰完全融化后,输入热量使液态水的温度上升,此时温度上升速率(曲线的斜率)与冰时不同。
- 汽化(100°C 平台):在 100°C 时,热量再次用于相变(汽化),这一阶段输入的热量叫做汽化焓(enthalpy of vaporization)。
- 气态(蒸汽)升温:水完全汽化后,输入热量让蒸汽升温
- 在图中的斜率定义为 $$\text{Slope} = \frac{\Delta T}{q} , \left[ = \frac{K}{\frac{J}{\text{mol}}} \right] $$ $$q = \frac{1}{\text{Slope}} \Delta T$$
- \(\frac{1}{\text{Slope}}\)其还有一个名字叫做Molar Heat Capacity \(C_P\),也就是Specific Heat Capacity比热容
Molar Hear Capacity 摩尔热容 #
$$q = \frac{1}{\text{Slope}} \Delta T = n C_P \Delta T$$
- q:热量
- n:物质的摩尔数
- \(C_P\):摩尔热容
- \(\Delta T\):温度变化
Specific Heat Capacity 比热容 #
$$q=mcΔT$$
- m:物质质量
- c:比热容