Last Edit: 18/11/24
Light #
- 当我们讨论为什么像聚甲基丙烯酸甲酯(PMMA)这样的材料能够透明,而像玻璃态金属或单晶金属(如硅和镍基合金)则是不透明的时候,理解光的本质及其与材料的交互作用是至关重要的。
- 材料是否透明,很大程度上取决于其电子结构,这决定了它如何吸收光
PMMA #
- PMMA we were able to have a transparent polymer because PMMA is 100 % amorphous
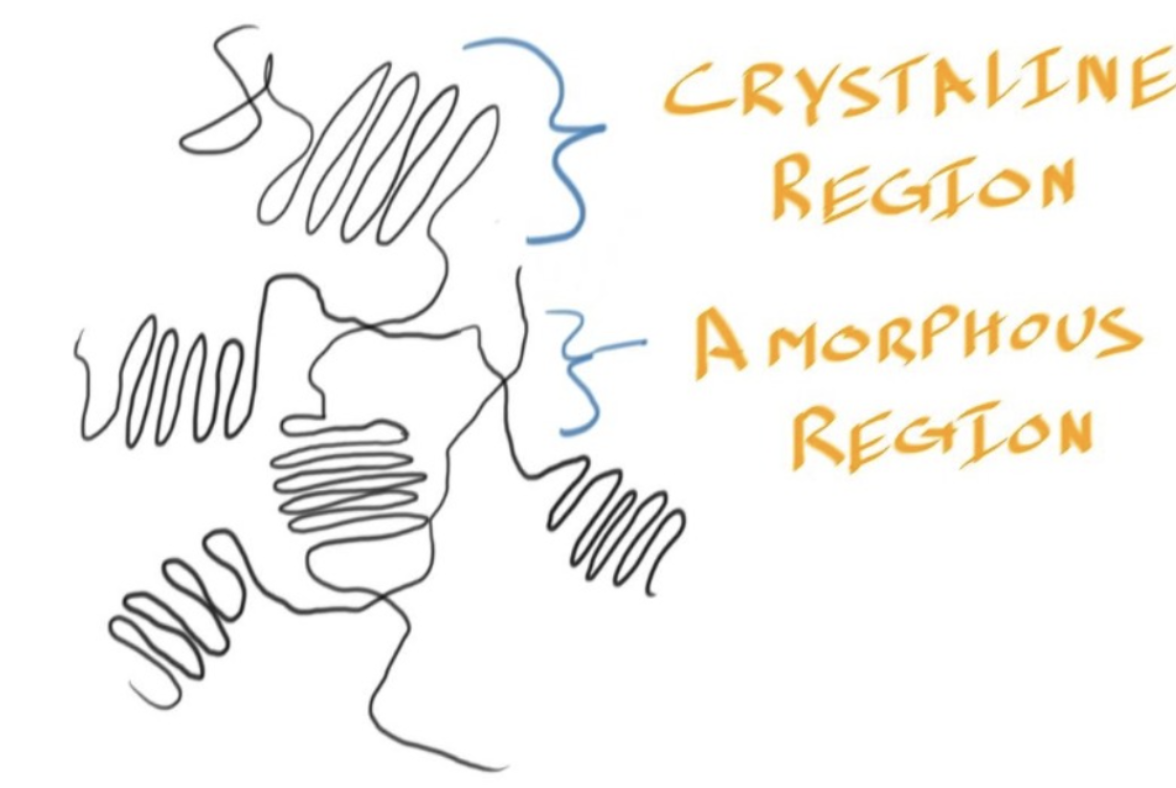
- 在非晶态的材料中,没有晶体和非晶体区域之间的界限,这种界限在晶体材料中可能会散射光线。
- PMMA中不存在这样的晶界,光线可以自由穿过,从而保持材料的透明性
Electromagnetic Spectrum 电磁光谱 #
- 可见光只是在包含了radio waves, microwaves, infrared radiation, ultraviolet radiation, x-rays, and gamma rays在内的大量辐射光谱中的极小部分
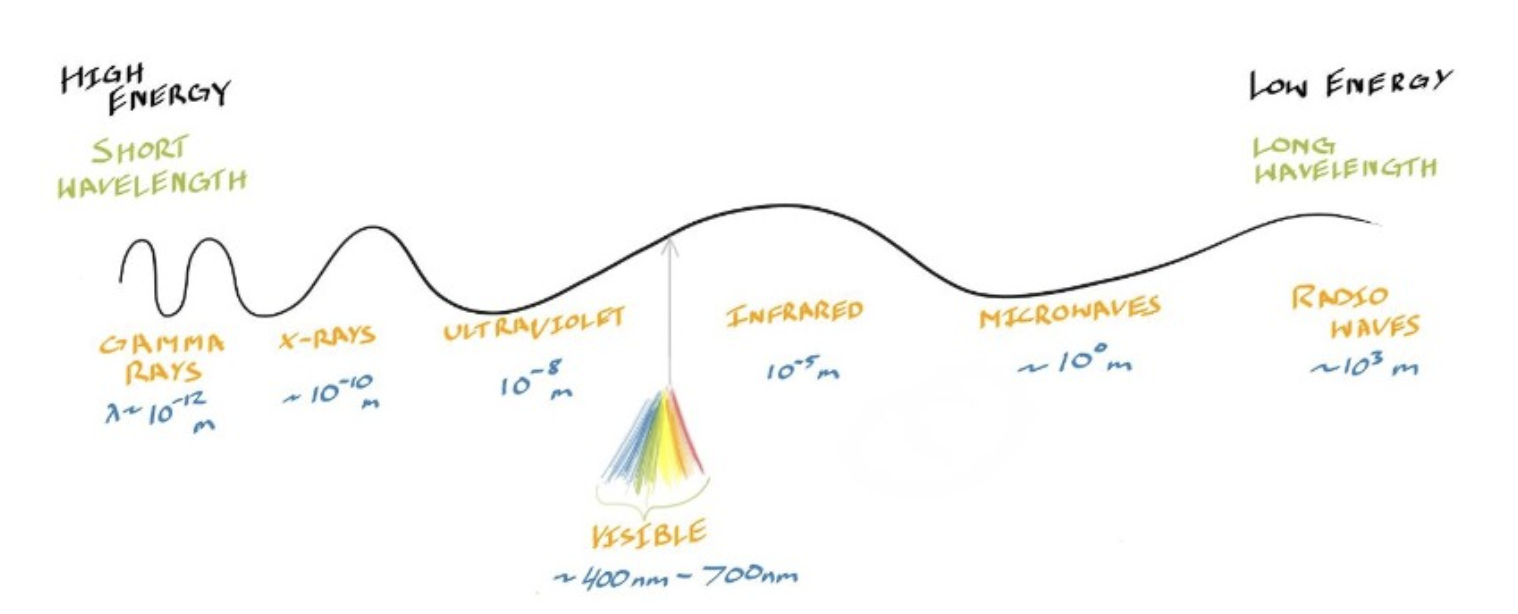
- 在# Electromagnetic Spectrum中,光子是Electromagnetic Radiation的基本粒子单位,承载能量和信息,跨越不同wave length的电磁波,包括无线电波、微波、红外线、可见光、紫外线、X射线和伽马射线
Electromagnetic Radiation 电磁辐射 #
Photons 光子 #
- 光子可以在空间中传播,不需要介质,是能量从一个地点传到另一个地点的方式
- 光的能量不是连续的,而是Quantized 量子化的
$$E = \frac{hC}{\lambda}$$
- \(h~(Plank~ ~Constant) = 6.626×10^{−34}J⋅s\)
- \(c~(Light~speed)=3\times 10^8 m\cdot s^{-1}\)
- \(λ~(Wavelength)~m\cdot s^{-1}\)
- 其更加常见的形式为 $$E=hv$$
- \(ν\) : frequency of the light in Hertz \((1 Hz = \frac1s)\)
Photoelectric effect 光电效应 #
- 由Albert Einstein于1905年提出
- 当光照射到金属表面时,光子将其能量传递给金属内的电子,如果这些光子的能量足够高,超过了金属的逸出功,电子就会被释放出金属表面
- 由于每个光子的能量由其频率决定,其能量和频率的关系则由公式\(E=hv\)给出
- 逸出功(Work Function):逸出功是指电子从固体表面逃逸到真空中所需的最小能量。不同材料有不同的逸出功。
- 光电子(Photoelectron):如果光子的能量高于逸出功,电子就会被释放,成为光电子
- 电子的动能(Kinetic Energy):释放的光电子将具有一个最大动能,这可以通过 \(Kmax=hf−ϕK_{\text{max}}\)来计算,其中 \(\phi\) 是逸出功
Wave-Particle Duality 波粒二象性 #
- 指物质(如光和电子)在某些情况下表现为波动性,而在其他情况下表现为粒子性。
- Photoelectric effect展示了光的粒子性,而光的波动性则通过其他实验如双缝实验(Double-slit Experiment)得到证明
Electron volt 电子伏特(eV) #
- 计算光子能量:使用的公式是 \(E = \frac{hc}{\lambda}\),
- 650纳米的红激光,将其转换成米\(650 \times 10^{-9} \text{ m}\),计算得到的能量是 \(3.06 \times 10^{-19}\)焦耳
- 虽然结果是正确的,但由于在量子力学和粒子物理中常常处理非常小的能量数值,使用焦耳(Joules)单位可能会显得笨拙和难以理解
- 于是引入了Electron Volt的概念
- 电子伏特是基于电子通过1伏特电势差加速后获得的能量。一个电子伏特定义为 \(1.602 \times 10^{-19}\) 焦耳
- \(E_{\text{Red Photon}} = \frac{3.06 \times 10^{-19} , \text{J}}{1.602 \times 10^{-19} , \text{J/eV}} = 1.91 , \text{eV}\)
Atom 原子 #
- 一个基本的Atom Structure可以概括如下
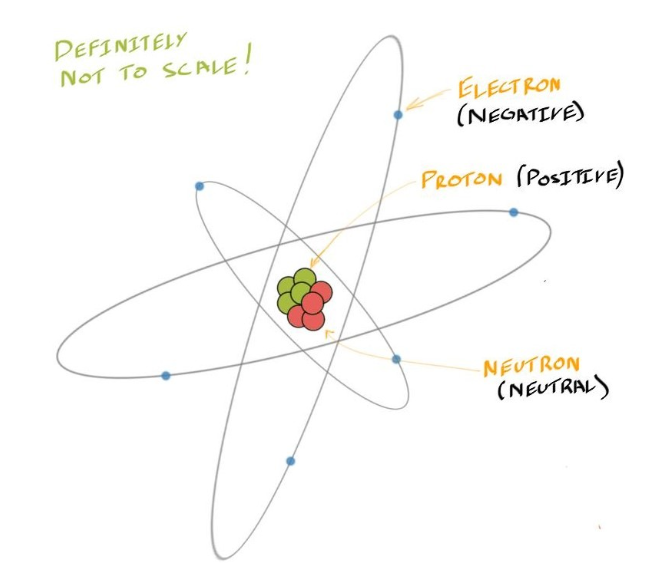
- Most of the mass of an atom comes from the nucleus 原子核
Isotopes 同位素 #
- Number of proton in nucleus决定了原子是什么元素
- 所以# of Protones也称为Atomic Number 原子序数
- 如Carbon-14, 写作\(C_{14}\)
- 对于6个Proton来说是Carbon,5个是Boron 硼,7个是Nitrogen 氮气
The Bohr Model of the Atom 原子的玻尔模型 #
- 历史上出现了许多个不同的Atom Structure
- 第一个取得了重大进展的则是Bohr Model
- 玻尔模型的基本特征是中心核和轨道电子,电子与原子核以固定的距离运行
- 能量跃迁:电子可以通过吸收或释放一个量子(quanta)的能量,从一个轨道跳跃到另一个轨道。这个能量的量正好等于两个轨道之间的能量差
Limitation 局限性 #
- 适用范围:波尔模型只能准确地计算具有一个电子的原子,如氢原子(H)、氦离子(He⁺)和双电离锂离子(Li²⁺)的行为
The Quantum-Mechanical Model of the Atom 原子的量子力学模型 #
- 在现代量子力学模型中,我们需要使用Four quantum numbers来完全描述一个电子的状态
- 而在尼尔斯·波尔(Niels Bohr)的早期模型中,只使用了一个量子数
Principal Quantum Number 主量子数 (n) #
- Describes the size of the electron orbit 描述了电子轨道的大小
- 可以是any integer value beginning at 1
- 不同的壳层代表电子与原子核的平均距离不同,能量也不同。
- K shell 是当 n=1 时的电子层,这是最接近原子核的电子层,也是能量最低的壳层
- L shell 是当 n=2时的电子层
- M shell 是当 n=3时的电子层
Angular Momentum Quantum Number 角动量量子数 ℓ #
- 角动量量子数(有时也称为方位量子数)描述了电子**轨道的形状
- 角动量量子数可以具有比主量子数小 0 到 1 的任何值, that is \(ℓ=0,1,2,…n−1\)
- 当ℓ=0 时,轨道是球形的(s-轨道) s亚层可容纳 2 个电子
- 当l=1时,亚层是 p 轨道,形状是偶极形(类似哑铃)p亚层可容纳 6 个电子
- 当l=2时,亚层是 d 轨道,形状更加复杂,通常有四叶或更多叶的形状 d亚层可容纳 10 个电子
- 当l=3时,亚层是 f 轨道,形状更为复杂 f亚层可容纳 14 个电子
- 当 ℓ=1 时,轨道呈哑铃形(p-轨道)

- 更高的ℓ值对应更复杂的轨道形状
The Magnetic Quantum Number 磁量子数 ml #
- 磁量子数主要用于指定原子轨道在三维空间中的取向,并与外部磁场中的能级分裂有关
- Describes how many different ways each subshell can be orientated
- 磁量子数 mℓ 可以取从−ℓ到+ℓ的整数值,包括零,其中 ℓ是角动量量子数。这表示对于给定的角动量量子数,存在2ℓ+1个可能的磁量子数。
- 例如,如果电子处于p轨道ℓ=1,那么mℓ可以是 -1, 0, 或 +1,对应轨道在空间中的三个不同取向。
Spin Quantum Number 自旋量子数 (s) #
- 自旋量子数ms并不直观地描述电子的物理自旋,因为电子实际上并不是在空间中围绕某个轴物理旋转。
- 将电子描述为“旋转”的说法可能会引起误解
- 量子数值:自旋量子数的可能值为\(\frac{1}{2}\) 或\(-\frac{1}{2}\),通常表示为电子的自旋向上(up-spin)和自旋向下(down-spin)
Eletron‘s Spin 电子的自旋 #
- 电子的“自旋”这一术语实际上并不指电子在空间中像地球绕其轴旋转那样的物理旋转
- 电子自旋是一种量子力学性质,表现为一种内在的角动量
- 尽管这个性质被称为“自旋”,但它并不涉及电子在任何可见的或传统意义上的物理旋转
Summarize #
- 大概总结一下,对于一个电子,有四个变量能决定他的属性,也就是四个Quantum Numbers
- 这四个变量的由来是由Pauil Exclusion Principle规定的
- 即同一层级,同一轨道类型,同一轨道编号下最多存在两个电子
- 当四个Quantum Nubers 全部相同的时候,则两个电子一致
1. Principle Quantum Number 主量子数 #
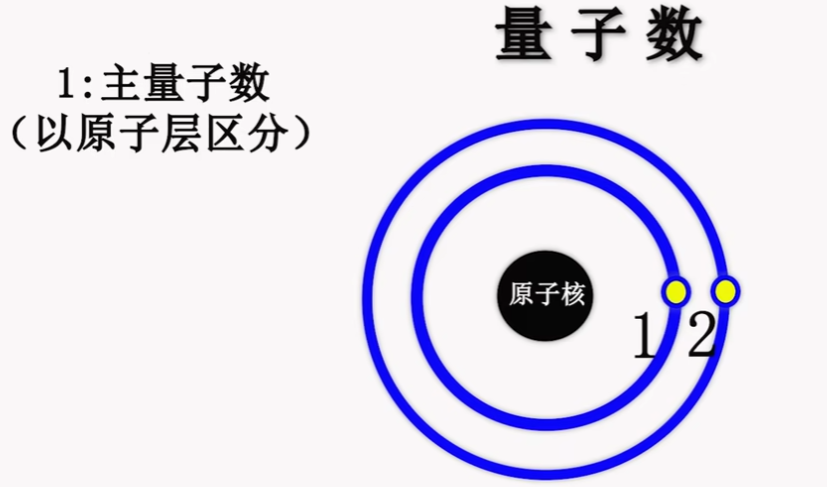
- 以电子所作在的电子层级区分
- n = 1 or 2 or 3 or 4 or 5
2. Angular Momentum Qunatum 角量子数 #
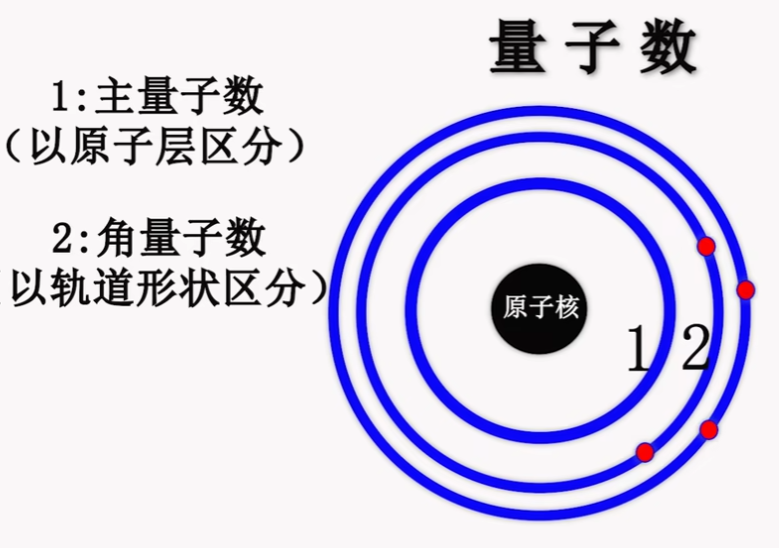
- 通过同一层级下的不同轨道(以形状)区分
- n = 2 & l = 1 or 2
3. Magnetic Quantum Number 磁量子数 #
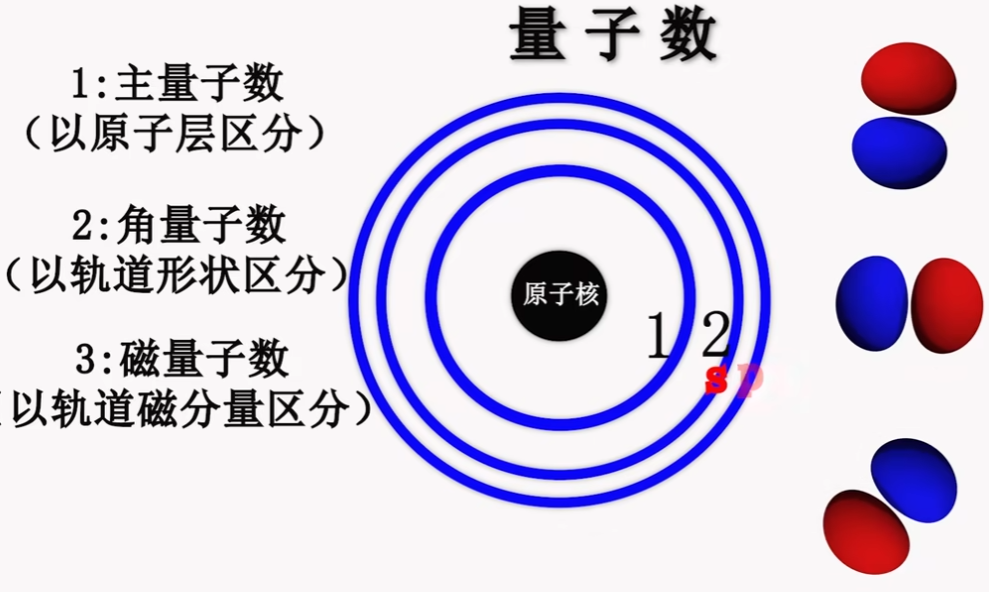
- 同一层级下,同一类型(形状)轨道,不同轨道编号区分
- n = 2 & l = 2 & m = -1
4. Spin Quantum Number 自旋量子数 #
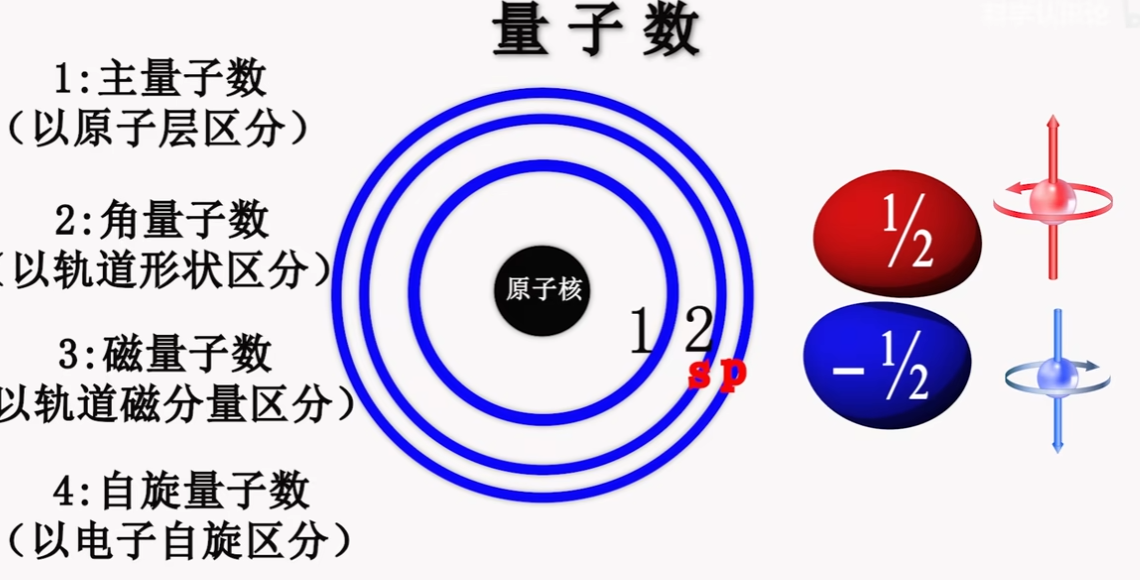
- 同一层级,同一轨道类型,同一轨道编号的不同电子
- 根据Pauil Exclusion Principle,同一层级,同一轨道类型,同一轨道编号下最多存在两个电子,其中一个上旋为1/2,下旋为-1/2
- n = 2 & l = 2 & m = -1 & s = 1/2
Electron Configuration #
- 但是想要描述一个元素的Electron Configuration,只需要描述到亚层就够了,每一个亚层都有它能存在的固定电子数
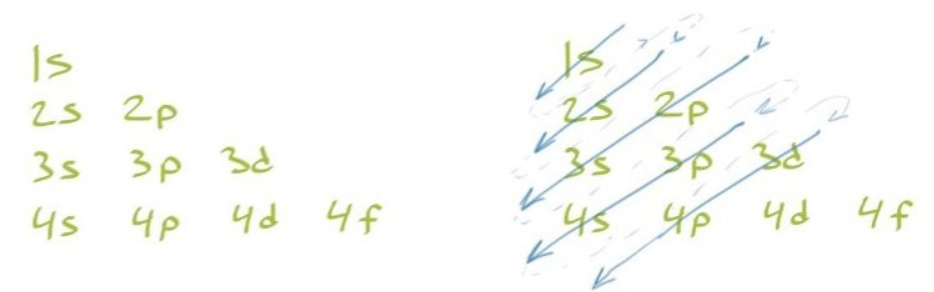
The Electron Configuration of Carbon #
- 元素周期表中可以确认,我们的老朋友碳的原子序数为 6,
- 这意味着一个碳原子的原子核中有六个质子
- 因此,要构建一个中性碳原子,我们需要将六个电子放入原子核周围的外壳和子壳中
- 要注意1s中的1是Pricipal Quantum Number,s是Angular Momentum Quantum Number
- 而且一个亚层是可以包含2个电子的,所以一个n = 2中的 l =1 的亚层p可以有6个电子,写作\(2p^6\)
- 那么对于Carbon来说就有 $$1s^2 , 2s^2 , 2p^2$$
- 有的时候为了省略,可以从该元素的前一个Nobel Gas的Electron Configuration开始写起
- 对于Carbon来说则是Helium $$[\text{He}] 2s^2 , 2p^2 $$
When 4s is Closer Than 3d Writting Format #
- 在上面的Electron Configuration里可以看到4s层的能量实际上是低于3d的,这主要是因为电子层级不是主要只依靠其Primary Quantum Number决定
- 但是在书写时统一按照了国际惯例,即按照Primary Quantum Number顺序书写
Physical Reason Under #
- 尽管在填充电子时,4s能量低于3d(因此4s轨道先填满),但在元素离子化或化学反应中,4s电子往往更容易被移除。
Titanium #
- 所以Ti的完整规定写法是 $$1s^2 2s^2 2p^6 3s^2 3p^6 3d^2 4s^2 ~ and ~ [\text{Ar}] 3d^2 4s^2$$
- 可以发现前一个的3d应该是10个,但只写了2个就到s了
Few Exceptions 特例 #
- 在3d亚层处于半满或全满状态时,即4,9时
- 系统可以通过重新分配电子来达到更稳定的状态
Vanadium #
$$1s^2 2s^2 2p^6 3s^2 3p^6 3d^3 4s^2$$
- 可以发现3d亚层只有3个,不处于即将Half-Filled or Completely Filled的水平
Chromium #
$$1s^2 2s^2 2p^6 3s^2 3p^6 3d^5 4s^1$$
- 4s(小于3d的层级)的电子被3d拿去了,以达到了Half-Filled的水平
Copper #
$$1s^2 2s^2 2p^6 3s^2 3p^6 3d^{10} 4s^1$$
- 4s(小于3d的层级)的电子被3d拿去了,以达到了Full-Filled的水平
Octet Stability #
- \(He=1s^2\)
- \(Ne=1s^2 2s^2 2p^6\)
- \(Ar=1s^2 2s^2 2p^6 3s^2 3p^6\)
- \(Kr=1s^2 2s^2 2p^6 3s^2 3p^6 4s^2 4p^6\)
- 可以发现,由于Nobel Gas的电子构型使其具有八电子(octet)结构,遵循八隅规则
- 所以他们的Electron Configuration通常可以表示为\(ns^2 np^6\)的形式
Ionic Bond #
离子键的形成过程 #
- Cl的Atomic Number是17,其电子构型为\(1s^2 2s^2 2p^6 3s^2 3p^5\)
- 它缺一个电子就可以达到Octet的稳定结构
- Na的Atomic Number是11,电子构型为\(1s^2 2s^2 2p^6 3s^1\) 或简写为 \([Ne]3s^1\)
- 它如果失去一个电子,也可以达到类似稀有气体的稳定构型
电子转移与离子形成 #
- 钠会失去一个电子,形成带正电的钠离子(Na⁺)。
- 氯会接受一个电子,形成带负电的氯离子(Cl⁻)。
- 这种电子的转移使得钠和氯都达到了稳定的电子构型,形成了Ionic Bond
离子键的特性 #
- 这种静电吸引力是non-directional,即在所有相邻的正负离子之间普遍存在,使得离子晶体结构非常稳定
- 在晶体中,所有电子都被紧密束缚在各自的离子中,不自由移动,因此固态的NaCldo not conduct electricity
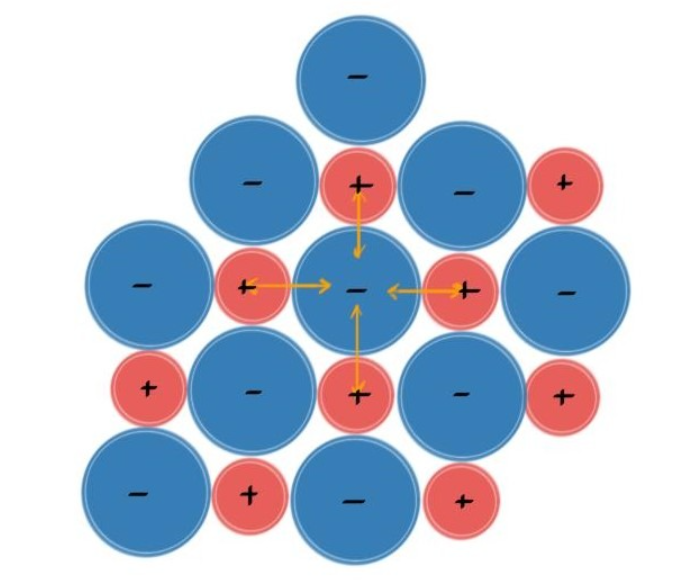
- 图中显示了NaCl晶体的结构,红色小球表示Na⁺,蓝色大球表示Cl⁻。
- 黄色箭头表示离子间的静电吸引力。
- 由于正负离子的规则排列,晶体内每个离子都被周围的异性离子包围,形成稳定的晶格结构
Colvaent Bond #
- Colvaent Bond涉及Electron Sharing,即原子通过共享价电子来达到稳定的Octet结构
- 甲烷(CH₄)是一个简单的例子:碳和氢通过共价键结合,形成一个稳定的分子。
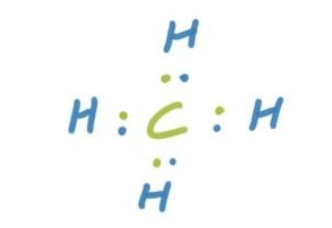
- 共价键只在Specific Atoms形成,例如在CH4中,Carbon仅与四个Hydrogen Bond形成共价键,而不会与其他原子相连。这种键称为Directional Bond
- 共价键的本质区别在于电子共享,而离子键则是电子转移
Metallic Bonding #
- 金属键通常用两种模型描述:sea-of-electrons model, and the band theory of solids
Sea of Electrons Model #
- 电子海模型中,Valence electrons不固定在特定的原子核上,而是自由移动,形成一个电子的“海洋”(sea of electrons)
- 要注意Inner electrons (non-valence electrons)是不在Electron Sea中的,因为他们并不参与反应
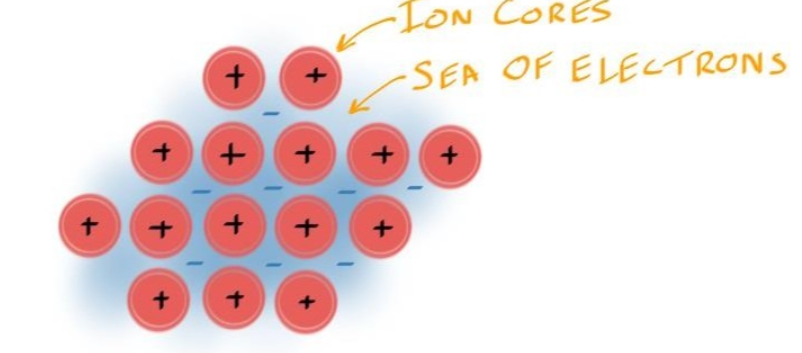
- Ion Core周围的蓝色区域全是电子
Valence electrons 价电子 #
- 原子最外层的电子,直接参与化学反应和形成化学键。它们决定了元素的化学性质,例如其反应性、与其他元素形成的键类型等
- 这些自由移动的电子使得金属具有Conductivity和延展性,因为电子可以在整个晶体中自由流动
Ion core 离子核 #
- 在金属或其他离子化合物结构中,不参与化学键的原子核和内层电子的组合
Conductivity of Sea of Electrons Model 导电性
- 模型中,electrons are free to move past the ion cores (or so-called delocalized) 离域化
- 自由移动的电子可以在金属内传导电流
- 相较于Covalent Bond来说,其被局限在特定原子之间,因此像聚合物这样的材料通常是电的绝缘体
Ductility #
- 金属晶体受到足够大的应力时,一个原子平面可以滑过另一个原子平面
- 在金属中,原子是按照晶体结构排列的,周围有自由移动的电子(电子海)
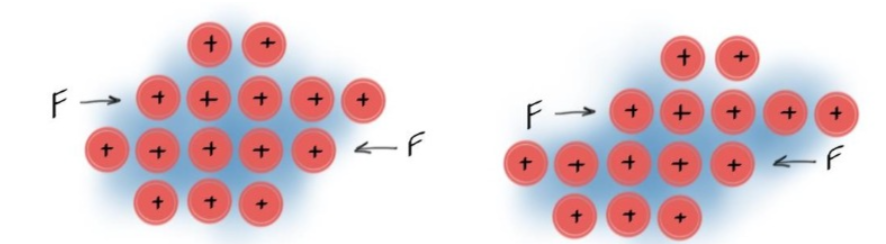
- 当对金属施加较大的力(如拉伸力或剪切力)时,金属中的一个原子平面会滑动到另一个原子平面之上
- 即使发生滑动,由于电子海的存在,这些自由电子能够迅速重新分布并填补原子之间的空隙,从而保持金属的整体结构稳定,不会断裂
Ceramic #
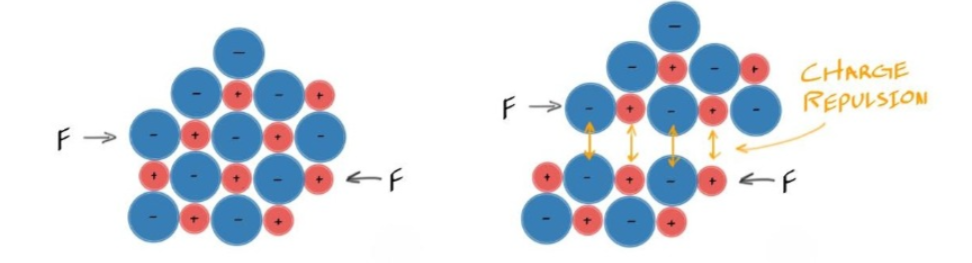
- 而对于Ionic & Covalent Bonding来说,由于其结构性,导致一旦发生了滑动,其负电荷会和负电荷处于同一平面导致Repulsion
- 在陶瓷材料中正负离子交替排列形成晶体结构。
- 当试图使一个原子层滑过另一个时,同性电荷的离子(例如两个正离子或两个负离子)会短暂靠近。
- 同性电荷靠近时会产生强烈的静电排斥力。
- 结果:导致了陶瓷在变形前就会发生脆性断裂。
Polymer #
Duality #
- 聚合物主要通过covalent bonds将分子内部连接,而分子间的连接靠次级键(如范德华力或氢键)。
- 在塑性变形中,Secondary Bonds被克服,聚合物分子链滑动,而共价键不会断裂。
- 结果:聚合物表现出较大的可变形性(如韧性),而不会像陶瓷那样容易断裂。
Conductivity #
- 聚合物中,all of the valence electrons are tightly bound in the strong covalent bonds
- due to the lack of any free electrons
- 聚合物是electrically insulating
Form of Crystal of Salt #
I know that NaCl forms an ordered solid, but why?
- 这是因为物质趋向于从things tend to proceed from higher energy to lower energy
- 当某些事情发生(如盐形成晶体)是因为这样的状态对能量来说是更“有利”的,也就是“lower energy” $$Na_{(s)} + \frac{1}{2}Cl_{2(g)} \rightarrow NaCl_{(s)}$$
- 对于上面的反应,我们将其拆分成子反应
Sublimation of Sodium 钠的升华 #
$$Na(s)→Na(g)$$
- 固态钠\(Na_{(s)}\)直接转化为气态钠原子\(Na_{(g)}\),称为升华(sublimation)
- 这种物质从固体转变为气体的过程需要能量,称为升华焓\(\Delta H_{\text{sublimation}}\),对于钠为\(ΔHsublimation=109kJ/mol\)
- 这里正值代表了:系统需要吸收能量便反应从左向右进行
- 也就是说,需要能量来熔化然后煮沸钠
Ionization of Sodium Atom 钠原子电离 #
- 气态钠原子\(Na_{(g)}\)进一步被电离为钠离子\(Na^+_{(g)}\)和一个电子\(e^-\) $$Na(g)→Na(g)^++e^−$$
- Ionization energy is \(IENa=497kJ/mol\)
- 可以发现这目前还是一个Posititve,则代表还需要吸收能量
Bond Dissociation of Chlorine Molecule 氯的解离 #
$$\frac{1}{2}Cl_2(g)→Cl(g)$$
- \(BDE_{Cl_2} = 121 , \frac{kJ}{mol}\)
- 这仍然是吸热过程(需要能量输入)
Formation of a chlorine anion #
$$Cl(g)+e^−→Cl(g)^−$$
- 这一过程中的Electron Affinity为\(EACl=−364\frac{mol}{kJ}\)
- 可以发现能量第一次变为了负的,这是第一个释放能量的步骤
Forming the ionic crystal #
$$Na(g)+Cl(g)^−→NaCl(s)$$
- 这一个过程包含了Crystallization energy\(Ecrystallization=−777\frac{mol}{kJ}\)
- 可以发现这一步消耗了很多能量
- 如果我们将这些能量项中的每一个相加,形成 NaCl 的总能量变化为−414
虽然第一步是吸热的,但整个反应通过后续的强烈放热步骤补偿了这一点。整体反应的自由能变化 (ΔG\Delta GΔG) 是负的,因而是自发的。这解释了为什么钠和氯最终可以自然形成盐晶体
The Band Theory 能带效应 #
电子能级由于相互的排斥作用发生分裂
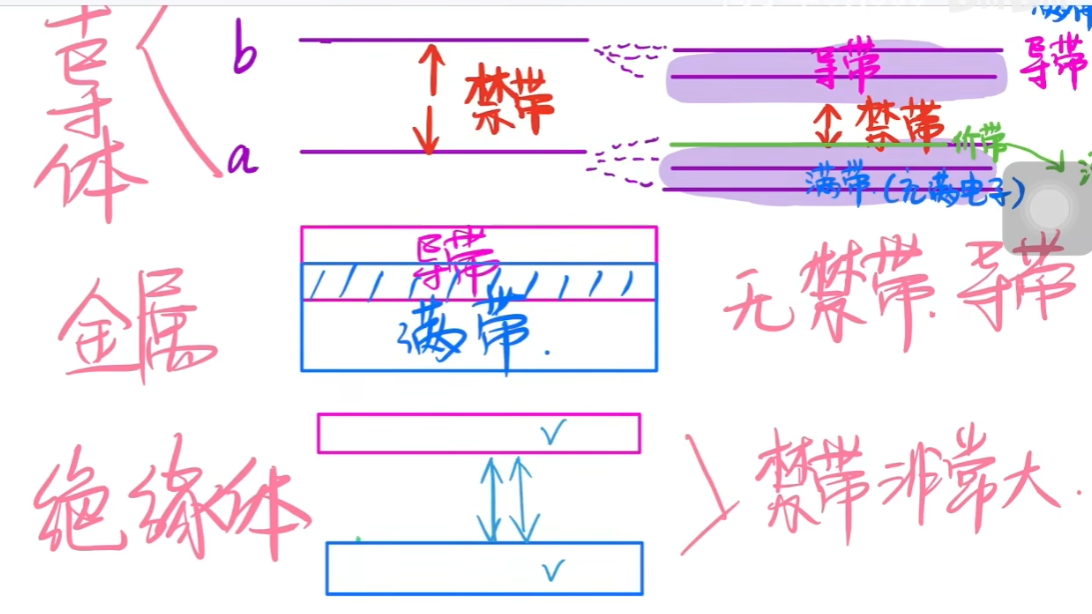
- 在孤立的原子中,电子能量被量子化,存在于离散的能级中(如s,p,d,f轨道)
- 这些能级之间的能量差是固定的,不会受到其他原子的影响。
- 对于每个原子原本的一个能级,靠近后会产生多个稍微不同的能级。
- 例如:对于两个原子,一个能级会分裂成两个能级;对于N个原子,会分裂成N个能级
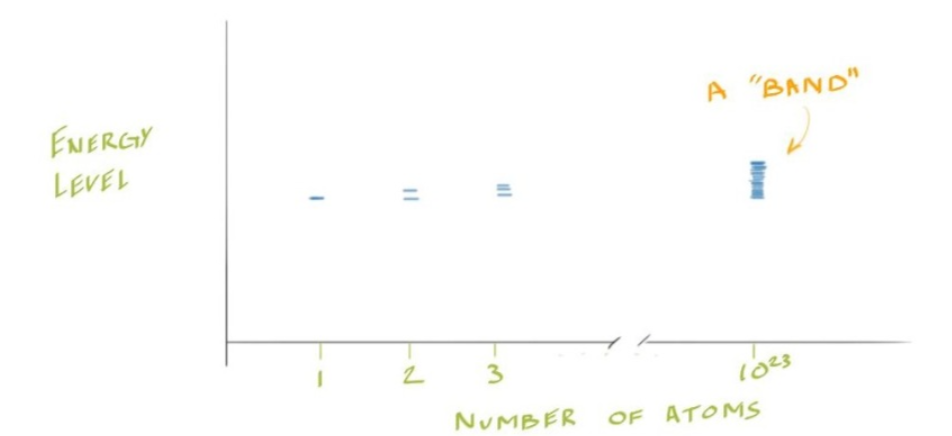
- 在固体中,原子之间的距离非常近,并且一个晶格中会有\(10^{23}\)个原子
- 原子的数量极其庞大时,原本分裂的离散能级数量非常多,且间距变得极其微小,最终看起来像是连续的能量区域——这就是能带(Energy Band)
- 原子越多,能带越“密集”
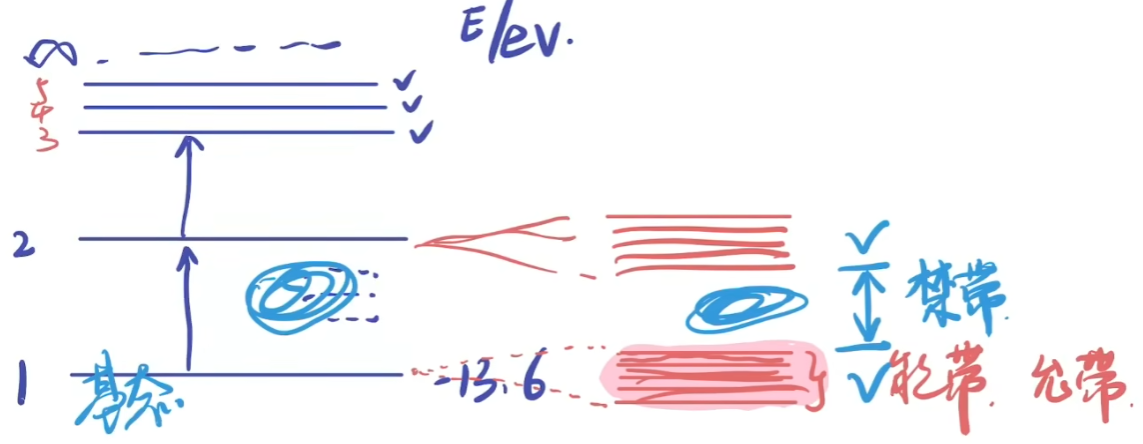
- 当对于一个原子,其存在多个能级,但当多个原子组合在一起的时候,电子的能量状态不再是离散的,而是形成了一个几乎连续的能量区域
- 孤立原子:电子有固定的、离散的能量(如轨道能级 s,p,d)
- 固体中:原子靠得很近,电子能级由于相互的排斥作用发生分裂。
- 分裂后的能量状态数量非常多,间隔非常小,看起来像是连续的,这就形成了能带
Bonding in Metals Like Copper #
- 用Copper的Electron Configuration举例 $$Cu =1s^2 , 2s^2 , 2p^6 , 3s^2 , 3p^6 , 3d^{10} , 4s^1$$
- 在4s中的两个Sublayer中只存在一个电子
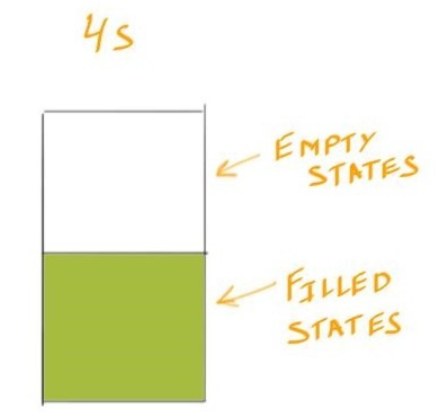
Conductivity #
- 导电的本质是低能量跃迁的累积:导电依赖于大量电子在价带和导带之间进行低能量的跃迁。如果3s电子要跃迁到4s或4p,势必要消耗更多的能量,而这在常温下不容易实现。因此,这些高能跃迁对导电贡献很小,甚至可以忽略不计。
- 所以说当一个轨道中存在Empty States的时候,Valence Electron才能在其中跃迁
Bonding in Metals Like Magnesium #
- 对于Mg来说\(Mg=1s^2 , 2s^2 , 2p^6 , 3s^2\),从表面看,3s轨道已经完全填满,因此看起来它不应该有可用的电子来参与导电
- 但是可以发现3p轨道是空的,但它并不是不可用的
- 这就像在剧院里,空座位虽然没有人坐,但仍然在那里,可以被占用
- 可以被占用。3s轨道和3p轨道的能级相互重叠,因此电子可以从3s轨道很容易地被激发到3p轨道

Bonding in Ceramics and Polymers #
- 回想一下,Ceramic往往通过Ionic Bond结合在一起,而Ionic Bond涉及Electron在Atom间的转移
- 还要记住,这种电子转移的发生是为了让每个原子都能获得填充的Valence Shell
- 由于Valence Shell是填充的,因此没有紧邻填充态的电子能态。此外,这些电子与原子核紧密结合,因此没有自由电子
- Polymer也是如此,只是他是Covalent Bond
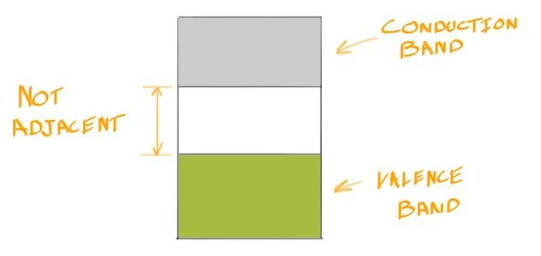
Valence Band 价带 #
- Valence Band是指电子填满的最高能量带
- 拿Si举例,其Electron Configuration为\(1s^22s^22p^63s^23p^2\)
- 其Valence Band即为\(3s^2\),3p虽然是最高能量带,但他并没有填充满
- 导电性:满带的电子不能自由流动,因为能量状态已经填满,没有空位供电子移动
Full Band满带 #
- Full Band是指电子完全填满的能量带。
- 在硅(Si)的例子中,\(1s^2 2s^2 2p^6\) 层被完全填满,这些内层电子构成了满带
- 这些满带主要是低能级的核心电子带,电子在这些带中被完全填满,无法参与到导电过程中
- 导电性:满带的电子由于能态完全填满,没有额外的空间或能级供电子跃迁,因此不参与导电。这些带在正常条件下对材料的导电性几乎没有贡献
Conduction Band 导带 #
- 导带是指紧邻满带之上的未填满能量带
- 拿Si举例,其Electron Configuration为\(1s^22s^22p^63s^23p^2\)
- 其Valence Band即为\(3p^2\)
- 当电子被激发到导带后,它们可以在材料中自由移动,从而参与导电
- Conduction Band通常是空的,或者仅有少量电子占据(在导体中可能存在部分填充)
- 导带中的电子是Valence electrons AKA Free Electrons,可以在材料中移动并产生电流
Simiconductor 半导体 #
- 一些材料,即半导体,具有的Bond Gap没有绝缘体那么大
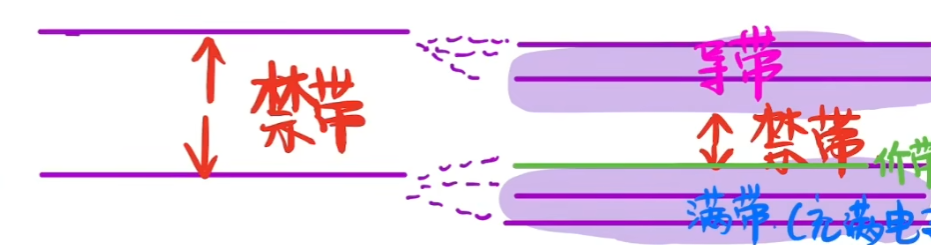
- 这很重要,因为这意味着我们可以控制这些材料中的电子流动。这是太阳能光伏、LED 照明和我们所有现代电子产品的基础
- 但大约 4 eV 通常是一个不错的数字。如果材料的带隙大于 4 eV,我们可以将其视为绝缘体,如果带隙小于 4 eV(但不为零)
Conductors, Insulators, and Semiconductors #
- 重新根据导电效率定义这三种的区别
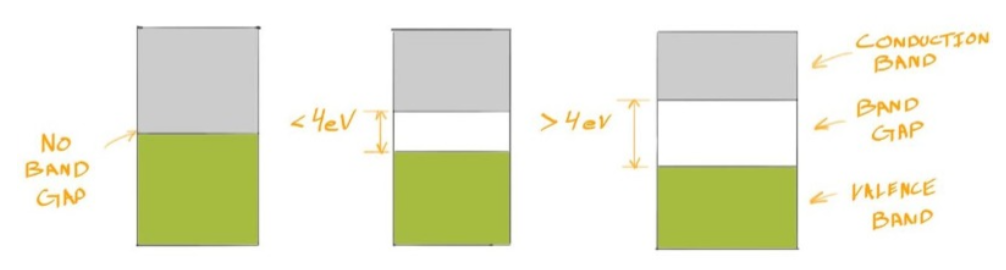
- 从左到右依次为 conductors semiconductors and insulators
Back To Light #
- 可见光由光子能量在 2-3 eV 之间的光子组成
- 如果材料的带隙大于 3 eV(例如 SiO₂,二氧化硅),那么可见光光子的能量不足以激发电子从价带跃迁到导带。
- 结果:光子通过材料时不会被吸收,因此材料对可见光是透明的。
- 举例:玻璃主要由 SiO₂ 构成,因此玻璃是透明的。
Energy efficiency of the building #
- 光穿过窗户进入室内会导致热量积聚,从而增加空调的能耗
- 解决方案:在窗户上镀金属薄层
- 金属薄层可以反射部分阳光(尤其是紫外线光子)。
- 如果金属层够薄,它仍然允许大部分可见光通过,同时减少紫外线和热量的传递。
- 优点:提高建筑的能源效率,降低室内过热问题。
Light & Metal #
- 金属的特点:没有明显的带隙(导带和价带重叠)

-
结果1:光子容易激发电子:
-
可见光光子的能量足够将金属中的自由电子激发到更高能级
-
因此,金属吸收光,并且是不透明的
-
结果2:金属的光泽(反射性):
-
被光子激发的电子会迅速返回到较低能量状态,在这个过程中重新发射光子
-
这种现象导致金属表面反射光,从而看起来有光泽(“金属光泽”)
Silicon 硅 #
- 实验表明,每个硅原子会形成 four identical bonds
- 但是,根据电子配置,3s 和 3p 轨道的能量不同,这意味着它们的性质不同
- 可以推出结论“Our model is limited. It can’t explain bonding in silicon”
sp3 Hybridization 轨道杂化理论 #
- 这里提出的解决方法是这样的:让我们只拿一个s轨道和3p轨道并将它们混合在一起
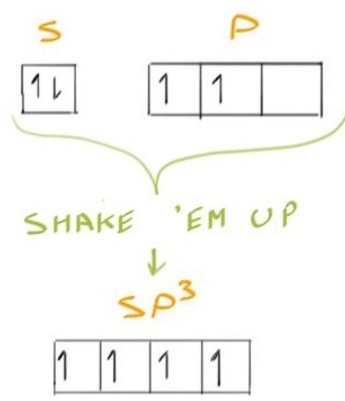
Diamond Cubic #
- 现在我们有四个等效的轨道,这些轨道的分布是对称的,彼此之间具有等价性
- it wouldn’t make sense for, say, three of them to be clumped close to one another and one bond to be all alone
- 也就是说,它们在空间中的位置分布是均匀的
Tetrahedral Configuration #
Semiconductors #
- 能够控制半导体的导电性对我们来说很重要
- 可以通过将杂质引入Semiconductors中以改变其导电性
Intrinsic Semiconductors 本征半导体 #
- 拿Silicon举例,其在3p轨道上,存在了4个Valence Electron
- 不同的Silicon则和其他的通过Covalent Bond组合成如下

- Intrinsic Semiconductors一种纯净的半导体,没有杂质掺杂
- 在Absolute Zero的时候可以形成如上图的结构
Hole 空穴 #
- 当温度上升了之后,Electrons会被Promoted进入Conduction Band导带
- 电子从Valence Band跃迁到Conduction Band后,会在原来的位置留下一个hole,即一个缺少电子的位置
- 其中,Electron和Hole空穴(电子缺失造成的正电荷)的数量是平衡的
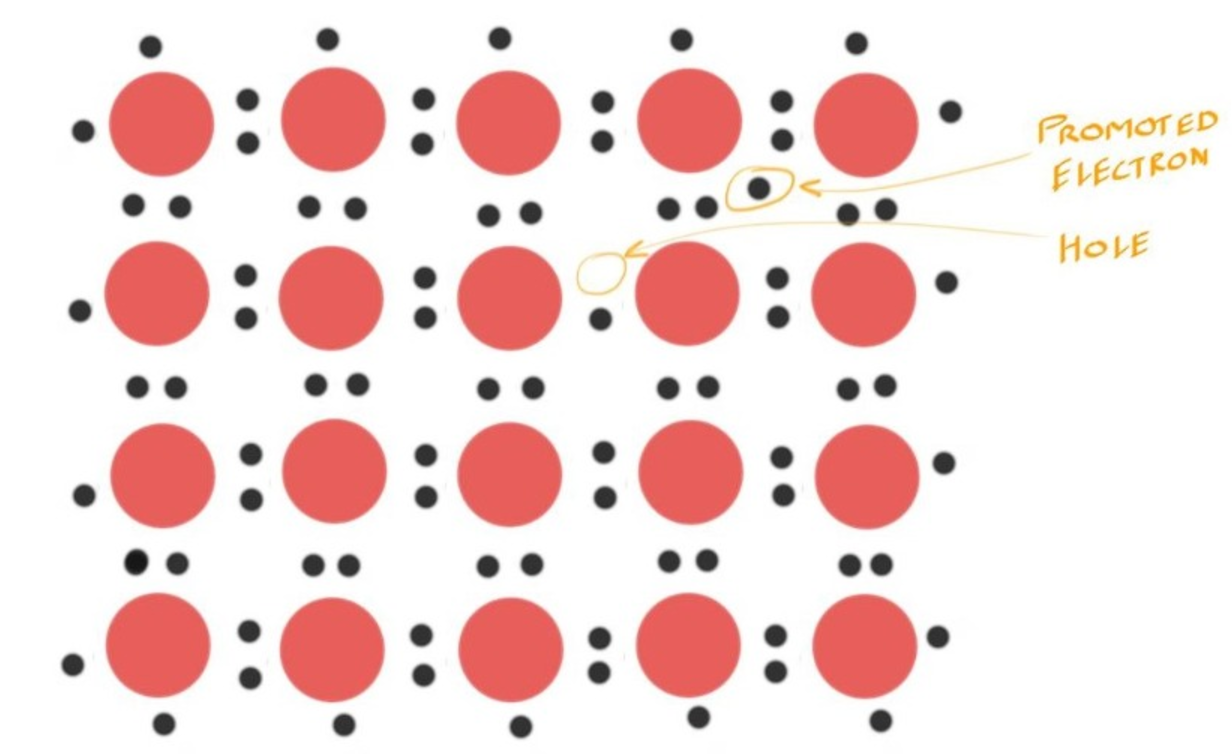
- 没多一个Electron被promote后,都会留下对应的Hole,亦可说他们是成对出现的
- 种类型的半导体称为Intrinsic Semiconductors,因为所有可用于导电的东西都来自半导体本身,而不是我们添加到其中的任何东西
- Intrinsic Semiconductors在实践中并不是特别有用,因为我们几乎总是添加杂质来控制Conductivity 电导率
Conductivity 电导率 #
- 计算一个Simiconductor的 Conductivity的公式为 $$\sigma = nq\mu_n + pq\mu_p $$
- 而对于Intrinsic Semiconductors的特殊情况来说,由于存在Concentration of holes = Concentration of electons,于是就有 $$\sigma = nq(\mu_n + \mu_p)$$
Concentration of electrons 电子浓度 n #
- Since electrons carry a negative charge
- 所以可以通过\(\frac{no
ofelectorns}{m^3}\)
Concentration of holes 空穴浓度 #
- 在本征半导体中,电子浓度(n)和空穴浓度(p)是相同的
- 这是因为Intrinsic Semiconductors中的电子和空穴都是由相同数量的价带电子激发到导带产生的
- 因此,在热平衡状态下,电子的生成和复合是平衡的,所以电子浓度和空穴浓度相等
Mobility 迁移率 #
- 对于Mobility来说存在Electron Mobility和Hole Mobility,分别通过\(\mu_n和\mu_p\)来表示
- 其单位为\(\frac{m^2}{V_s}\)
Charge 电荷 #
- Charge指的是Magnitude of the fundamental charge \(1.602\times 10^{-19}C\)
Extrinsic Semiconductors 外延半导体 #
- 本征半导体并不是特别实用,因为我们通常会向半导体中添加Impurities(称为dopants)以仔细控制其Conductivity
- 我们向半导体中添加Small amount of dopant的Dopants时,掺杂剂引入的电导率会压倒任何本征半导体,因此我们称之为Extrinsic Semiconductors
- 基本上存在两种加入Dopants的方式,使用额外的Electron或者Hole的方法
- 由于电子是Negataive Charged的,将添加Electron的叫做n- type Semiconductor
- 而Hole是Positive的(虽然其是Neutral的,但由于Hole存在于Electron的中间,所以看上去是“Positive”的),所以添加Hole的叫做p-type Semiconductor
Extrinsic n-Type Semiconductors 外本征n型半导体 #
- 想要在Intrinsic Semiconductor中添加Extra Electrons,可以通过Zero Dimension Inpurity的Point Defects来添加Inpurities Atoms,而添加的这一个Atom会带来额外的电子
- 已知对于Silicon来说其存在4个Valence Electrons:\(3s^23p^2\),一种合适的做法便是将位于元素周期表右侧的Atom加入,即一个存在5个Valence Electron的Atom,这便是P,磷
- 已知磷的Atomic Number为15,其Electron Configuration为\(1s^2 2s^2 2p^6 3s^2 3p^3\)
- 因此添加到硅晶格中时,当与相邻的硅原子形成四个共价键时,将有一个额外的电子踢来踢去
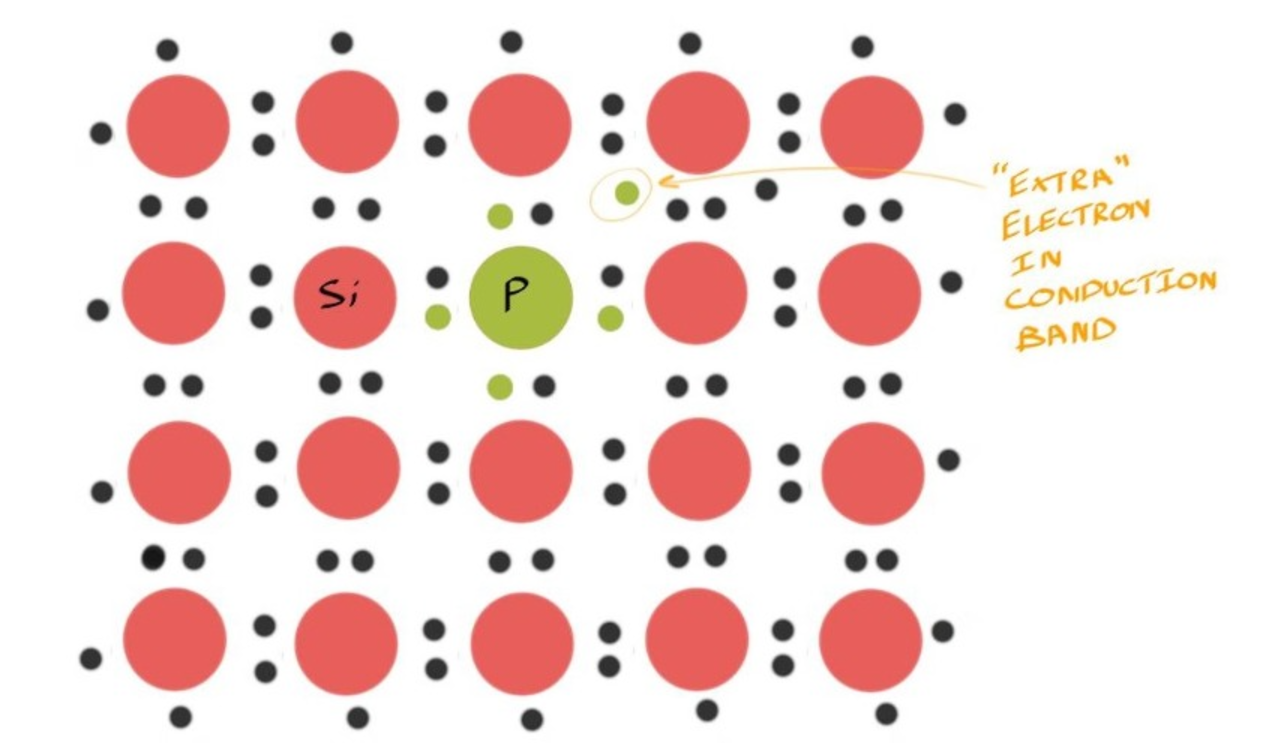
- 如上图所示,元素中出现了一个多余的电子,由于没有足够的周围硅原子来形成稳定的共价键,因此这个电子不像其他共价键中的电子那样稳定地束缚
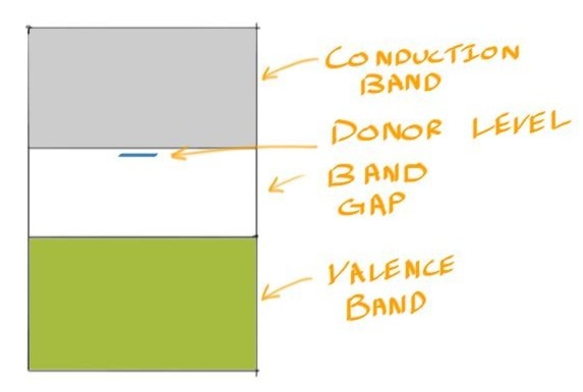
Donor Level供体能级 #
- 在Gap Band内,接近导带底部的蓝色线表示磷原子提供的额外电子的能级
- 这个能级非常接近导带,因此只需很少的能量就可以将电子激发到导带中。
- 由于Impurity P为Simiconductor贡献的 Charge carriers,亦或者说是价带比通过本征促进产生的电荷载流子多得多
- 因此我们可以忽略\(\mu_p\),只用电子浓度和迁移率来计算 n 型半导体的电导率 $$σ_{n−type}=nqμ_n$$
Extrinsic p-Type Semiconductors #
- 同理对于Silicon来说,选他左边的元素,B
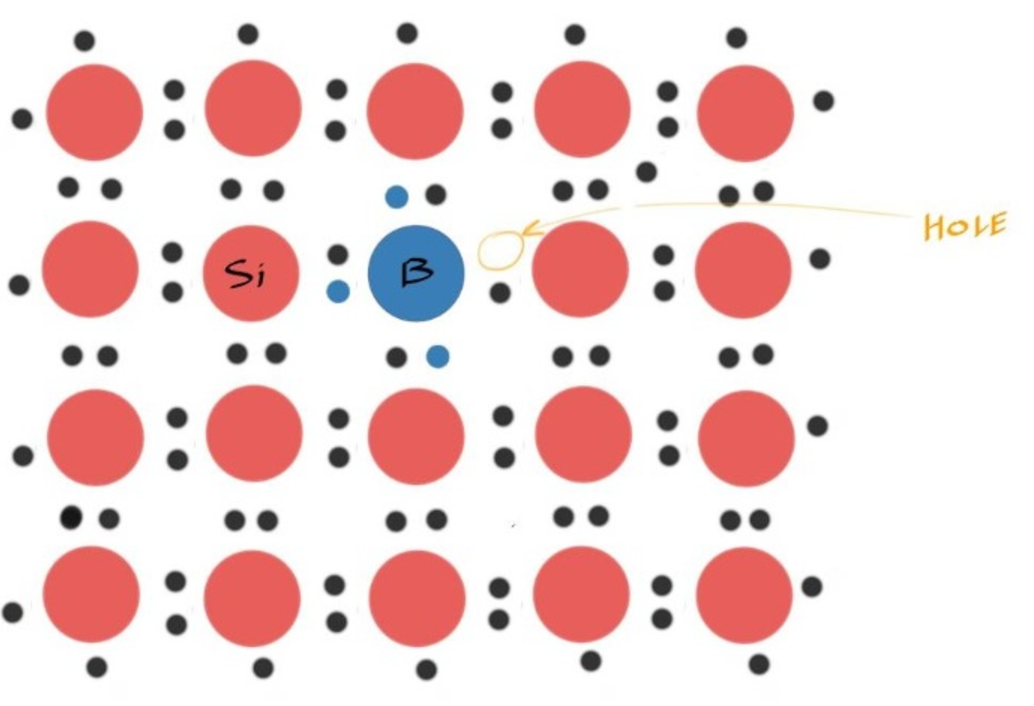
- 在Extrinsic p-Type Semiconductors中,电子不需要被激发到Conduction Band才能导电
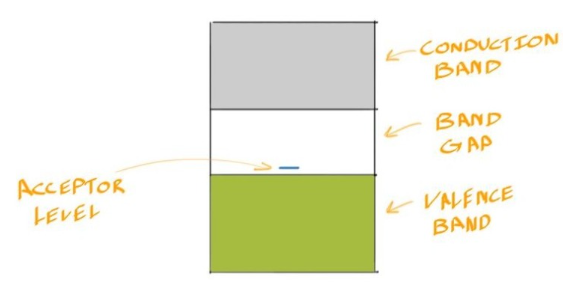
- 相反,价带中的电子可以轻易被激发到B提供的一个Hole上,从而填补那里的空穴,也就是Bnad Diagram上的Acceptor Level
- 同理可以忽略\(\mu_n\)的大小 $$σ_{p−type}=pqμ_p$$
Solid Ionic Conductivity #
- 当我们思考和谈论固体材料中的导电性时,我们会考虑电子的运动,就半导体而言,还会考虑“空穴”的运动
- 然而,导电性也可以通过Solid Ionic内的运动来实现