Last Edit: 9/25/24
Young’s modulus change with Density #
Ordered Solids #
- 大多数固体材料都是Polycrystaline 多晶体的
- 尤其是Metal在原子尺度上是按照Crystal Structure排列的
- Atomic scale尺度一般在\(10^{-10}\)的级别
Unit Cell #
- 最小的Convenient Building Block
Grains #
- 多晶材料的这些晶体被称为晶粒(grains)。每个晶粒内部的原子排列是有序的,但不同晶粒之间的原子排列方向各不相同,这种微观结构对材料的机械性能和物理性质有重要影响
Short Range Order #
- 指的是在局部区域内,原子或分子的排列是有规律的
- 玻璃、液体这样的材料,它们通常是Short Range Order的

Long Range Order #
- 在整个材料中,原子或分子的排列是有规律的,并且这种规律性会一直延续到较大的尺度(远远超过单个原子的范围)
- 晶体材料,如金属和矿物,通常具有长程有序

Simple Cubic #
- 简单的一个立方体上的八个角为Atoms的结构
- 其正方体的边长被定义为a
- n:1 Atom
- CN:6
- Side Dimension: \(a=2r\)
Hard Sphere Model #
- 所有的Atoms都被当作一个球来模拟,主要是方便描述原子在晶体结构中的排列方式
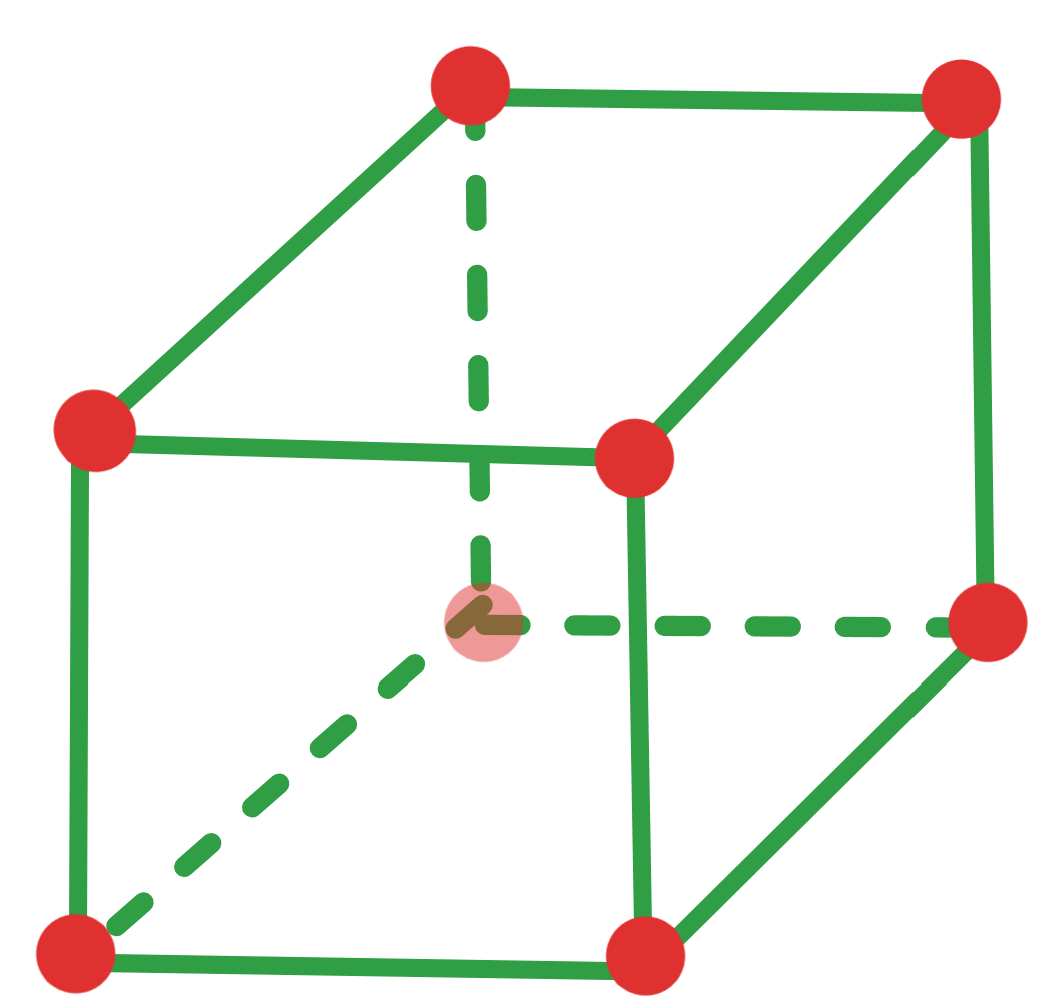
Reduced Sphere Model #
Real Graph #
- 可以发现这样的Hard Shpere Model看着实在是Messy
- 所以就将所有Atoms简化为Reduced Sphere Model
The Atomic Packing Factor 填充系数 #
- 对于一个Unit Cell,APF描述了Atom对于体积的占有率,从100%完全占据到0%一点没有 $$APF=\frac{Volume_{Spheres}}{Volumn_{Unit~Cell}}$$
- 本质上就是一个百分比或者说分数
- 现在分别计算两个体积
- 对于Spheres来说,单个的体积为\(\frac{4}{3}\pi R^3\),而将他乘上Number of Atoms后便可以得到所有的体积
- 对于Unit Cell来说,以a为边长,其体积自然为\(a^3\)
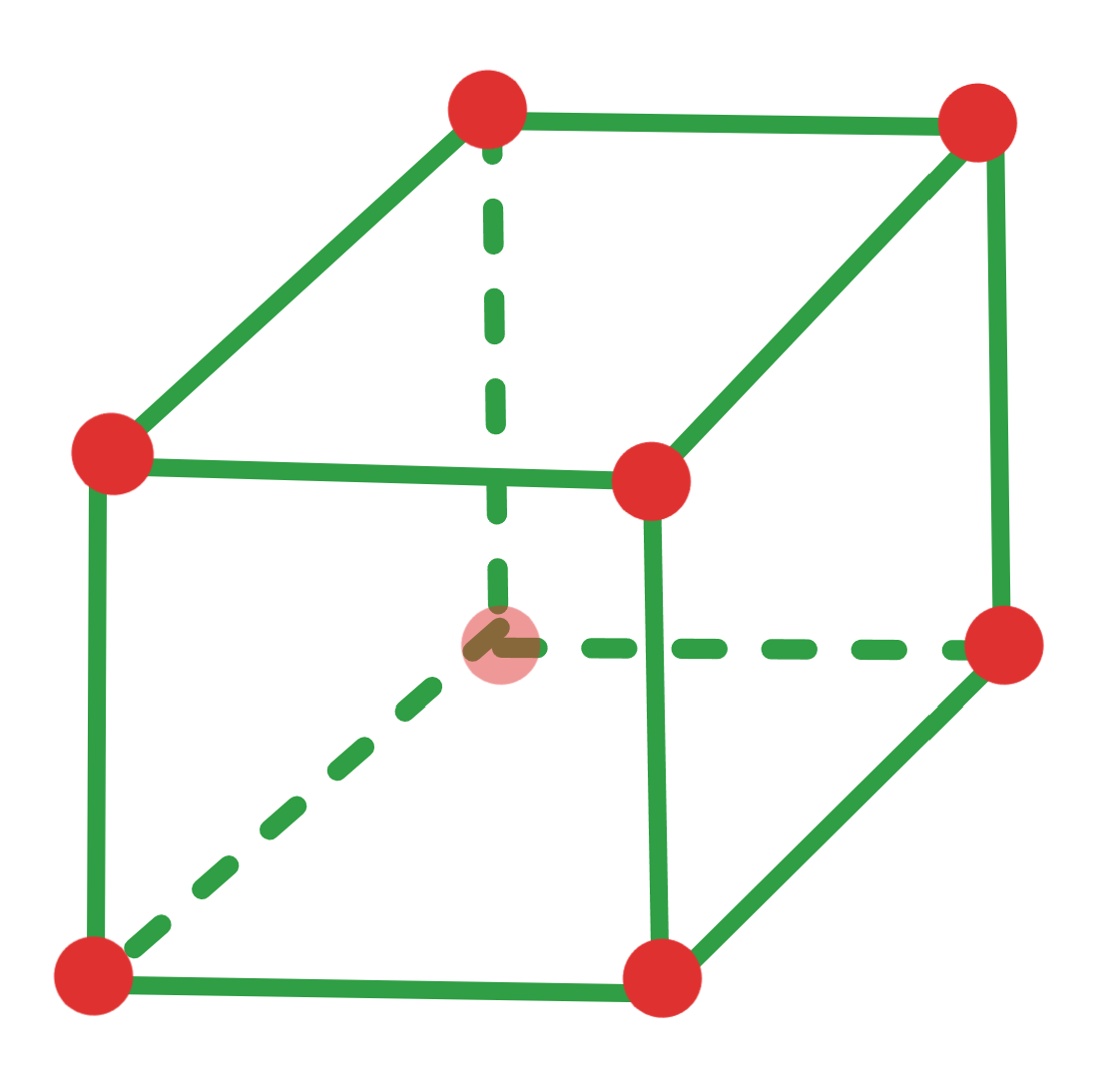
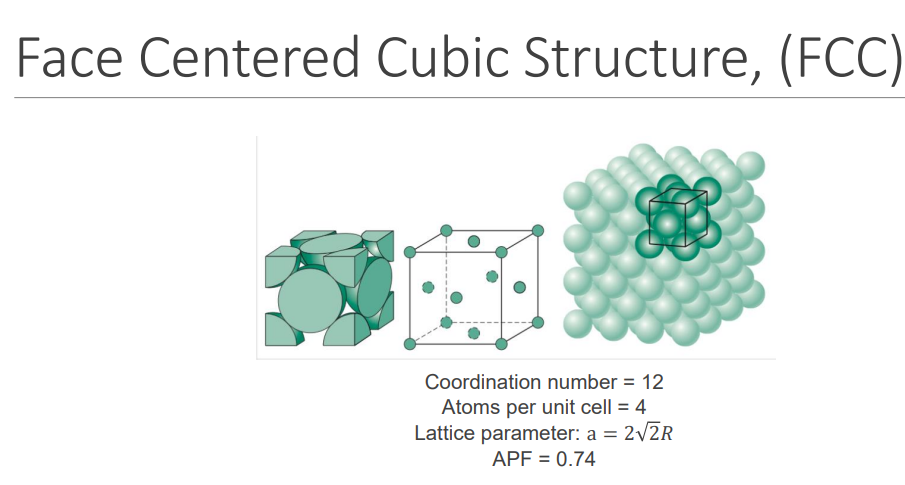
Face Centred Cubic (FCC) Structure #
- 结构特点:每个晶胞的八个顶点各有一个原子,此外每个面中心还有一个原子。
- n:每个晶胞含有 4 个原子(8 个顶点原子各占 1/8,6 个面心原子各占 1/2)。
- CN:12(每个原子有 12 个最近邻原子)。
- APF:约 74%(原子占据的体积比例)。
- 例子:铝、铜、金、银等
- 在Simple Cubic的基础上加入一些Face Centred Atoms(在每个面中心的Atom)
Number of Atoms in FCC #
- 对于FCC来说,每一个角上都是\(\frac{1}{8}\)个Atom
- 每一个面都有\(\frac{1}{2}\)个Atom
- 所以一共就是\(\frac{1}{8}*8+\frac{1}{2}*6=4\)个Atom
- 即\(n_{FCC}=4\)
Coordination Number of FCC #
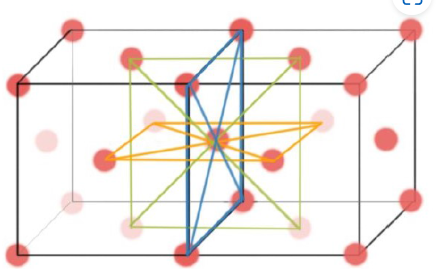
$$CN_{FCC}=12$$
Atomic Packing Factor of FCC #
- 则对于FCC Structure来说,其APF即为 $$APF=\frac{4\frac{4}{3}\pi R^3}{a^3}$$
- 现在要将Atom的radius与Unit Cell的边长a做替换好消掉其中一个
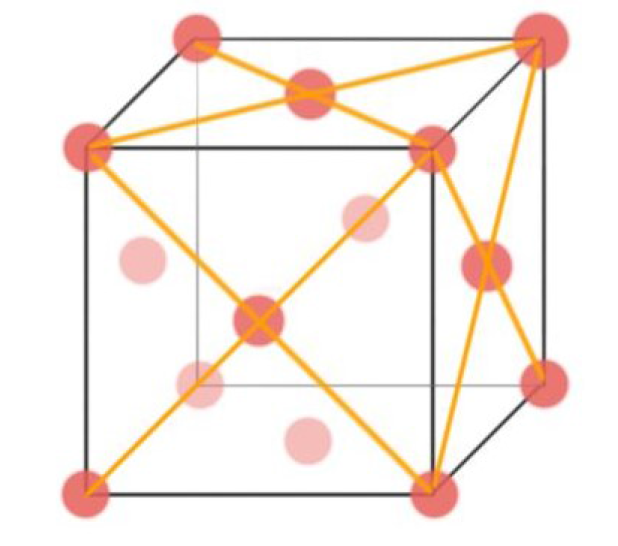
- 有\(a^2+a^2=(4R)^2\),勾股定律
- 则有\(2a^2=16R^2\),即\(a_{FCC}=2\sqrt{2}R\)
- 将a带入后便有 $$APF = \frac{4 \left( \frac{4}{3} \pi R^3 \right)}{(2\sqrt{2}R)^3} \ \Rightarrow APF_{FCC} = 0.74$$
Avogadro’s constant 阿伏伽德罗常数 #
- 通常用符号\(N_A\)表示,是指在1摩尔物质中包含的微观粒子(如原子、分子、离子等)的数量。其数值大约为:
$$N_A=6.022×10^{23 }g\cdot mol^{−1}$$
Theoretical Density 理论密度 #
$$\text{Mass}{\text{Atoms in Unit Cell}} = \text{Number}{\text{Atoms in Unit Cell}} \cdot \frac{\text{Molar Mass of Atom}}{\text{Avogadro’s Number}}$$
$$m = n \cdot \frac{A}{N_A}$$ $$\rho = \frac{nA}{V_C N_A}$$
- Density密度,即质量和体积的比值
- \(n\):Number of Atoms,一个Crystal里的完整分子个数
- A: Molar Mass(g/mol),原子相对质量
- \(V_c\):Unit Cell的体积
- \(N_A\):阿伏伽德罗常数\(mol^{-1}\)
- \(\frac{A}{N_A}\):\(\frac{g/mol}{mol^{-1}}=g\),等于一个Atom有几g,再乘上Atom Nuber得到全部的Mass
Rock Salt Structure #
- 是一个Common Ceramic的Crystal Structure
- 结构特点:这是离子晶体结构,通常由两种不同大小的离子(如Na⁺和Cl⁻)组成。大的离子(Cl⁻)形成一个面心立方(FCC)结构,小的离子(Na⁺)填充在八面体间隙中。
- A:每个晶胞含有 4 个阳离子和阴离子。
- CN:阳离子和阴离子的CN都为6。
- APF:约 67%。
- 例子:氯化钠(NaCl)、氧化镁(MgO)等。
- 对于Ceramic Structure来说,其拥有多余一种的Atom类型,具体来说有Cation和Anion两种
- 其是Ionic Compound的一种特有的Crystal Structure
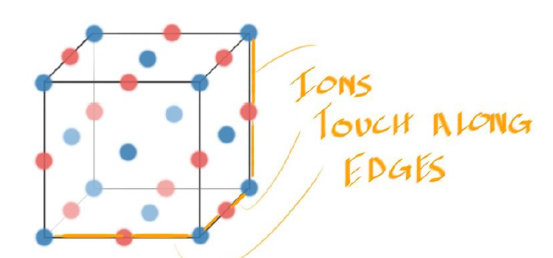
- 对于Rosk Salt Structure来说,其包含了两种Ion,即Anion(蓝色)与Cation(红色)
- Anions在Unit Cell的角上(Cation也可以在,他们描述的将是同一种结构,但一般来说体积大的Anion会先占据Unit Cell的角落,将小的Cation挤到中间去)
- 这个结构看起来像面心立方(FCC),但实际上不是纯粹的FCC,因为阳离子和阴离子之间有相互作用,会推开阴离子,使得阴离子不会像真正的FCC结构那样直接通过面对角线相互接触。
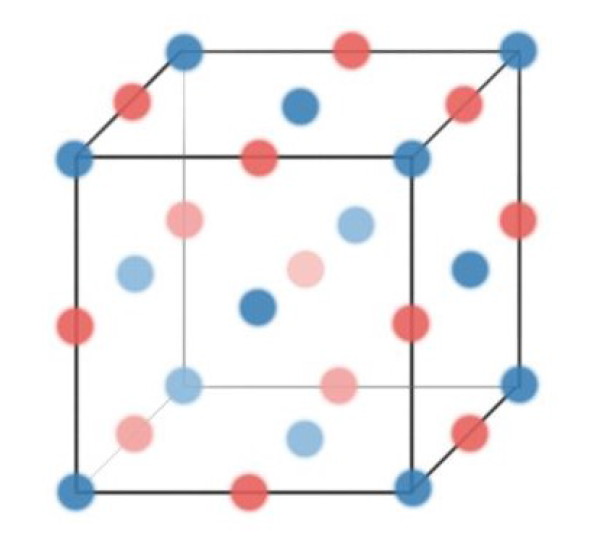
Number of Atoms in Rock Salt (Stoichiometry) #
- 对于如NaCl这样的material,其Anion:Cation比都是1:1的,但上图中明显缺少了一个Cation
- 其正确的位置应该是整个Unit Cell的正中央
Coordination Number for Cations in Rock Salt #
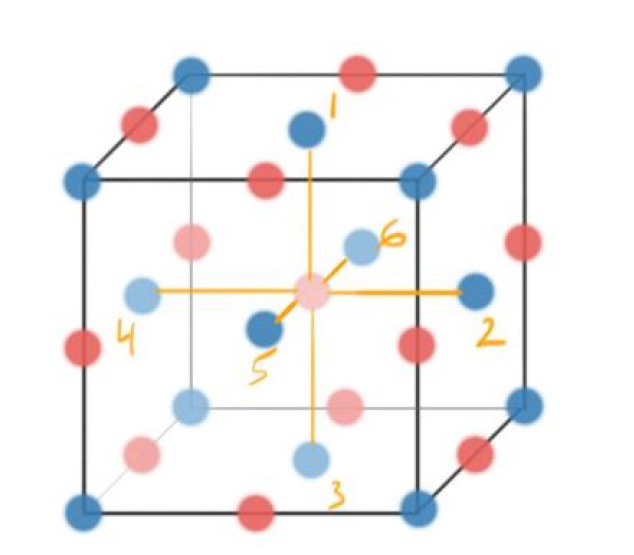
- 对于一个Rock Salt来说,拿最中间的Cation举例,可以发现与其接触的Atom有6个
- 于是就可以说\(CationCoordinationNumber_{Rock~Salt} = 6\)
Density of Rock Salt #
- 对于Rock Slat Structure来说,由于其Atom种类变为了Anion与Cation两个,其[[#Theoretical Density]]的分子也要对应的便为两个的和,即 $$\rho=\frac{n_CA_C+n_AA_A}{V_CN_A}$$
- \(n_CA_C\):Cation的Number和Moalr Mass,nA同理
- 对于Vc来说,其a变为了两个Atoms的Radus*2,有\(V_C=(2R_A+2R_C)^3\)
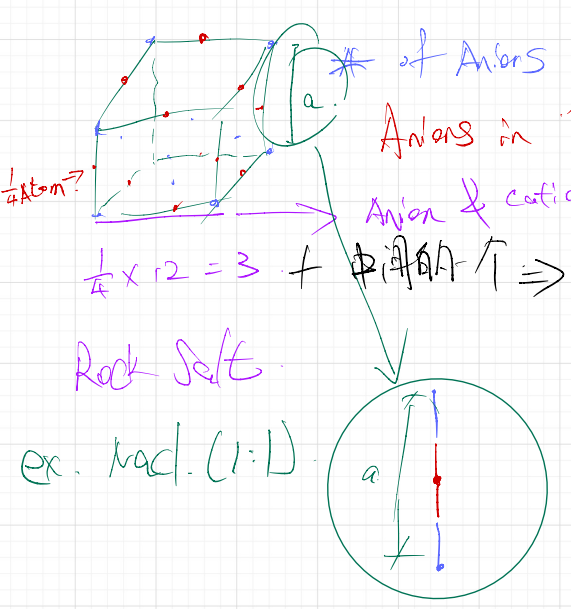
Theoretical Density of Rock Salt #
$$\rho = \frac{n_C A_C + n_A A_A}{V_C N_A}$$
Anions #
- 在Rock Salt Structure中的Anion看似处于FCC的位置中
- 但实际上由于附近的Cation和不同Anion之间的相互作用力导致Anion实际上不在精确的FCC位置上
Cations #
- the cations will always touch their nearest neighbour anions
The Body Centred Cubic Crystal (BCC) Structure #
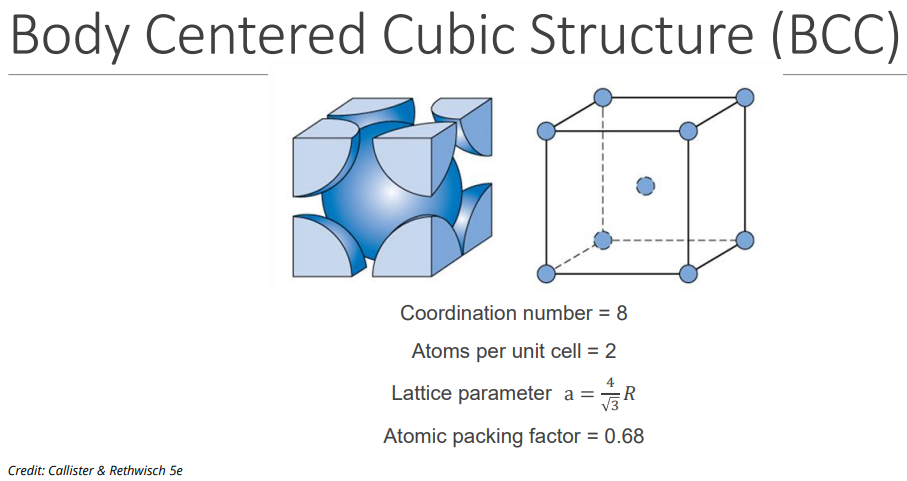
- 结构特点:每个晶胞的八个顶点各有一个原子,且晶胞中心还有一个原子。
- n:每个晶胞含有 2 个原子(8 个顶点原子各占 1/8,中心原子占 1 个)。
- CN:8(每个原子有 8 个最近邻原子)。
- APF:约 68%。
- 例子:铁、钨、铬等。
Number of Atoms in BCC #
$$\frac{1}{2}*2+\frac{1}{8}*8=2$$
Coordination Number of BCC #
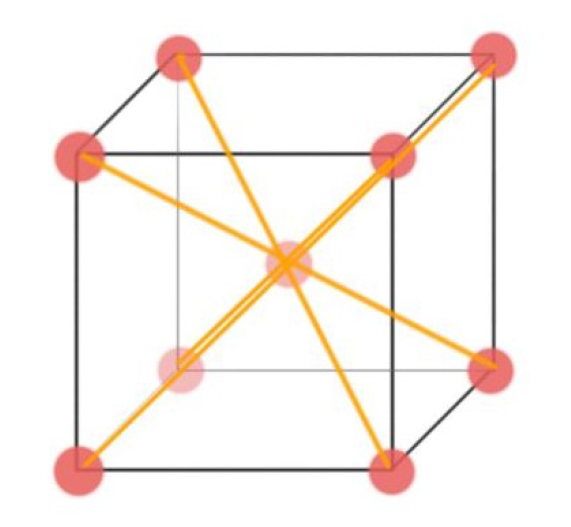
$$CoordinationNumberBCC=8$$
Atomic Packing Factor for BCC #
$$APF=\frac{Volume_{Spheres}}{Volumn_{Unit~Cell}}$$
- 对于BCC,要取其Unit Cell边长与Atom radius关系得用Cubic Diagonal,即 $$3a^2=16R^2,\Rightarrow a_{BCC}=\frac{4}{\sqrt3}R$$ $$APF = \frac{2 \left( \frac{4}{3} \pi R^3 \right)}{(\frac{4}{\sqrt3})^3} \
\Rightarrow APF_{BCC} = 0.68$$
Interstitial Sites #
- Space between other atoms
- 其体积就代表了Crystal Structure中的间隙的部分
- By convention, we name interstitial sites according to the solid geometry that they create
Octanhedron Interstitial Site #

- 对于Rock Salt中的Anion的Interstitial Sites,将他们命名为Octanhedron Interstitial Site
Coordination Number of a Interstitial Site #
- 对于Interstitial Site来说,其CN代表了Interstitial Site中心点位置的Atom与最近Atom接触的个数
- 对于Rock Salt来说,Intersitital Site CN = 6
Simple Cubic Interstitial Site #
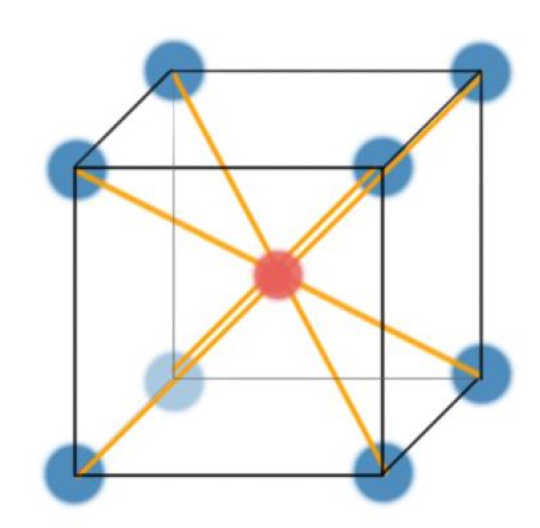
- 结构特点:每个晶胞的八个顶点各有一个原子,顶点原子通过边连接,但面心和体心没有原子。
- n:1Atom(8 个顶点原子各占 1/8)。
- CN:6(每个原子有 6 个最近邻原子)。
- APF:约 52%。
- 例子:钋(唯一的自然存在的例子)。
- 纯的简单立方晶格中,中心位置是空的(这个红点代表的就是Intersititial Site间隙位的大小
- 但在体心立方或其他某些间隙结构中,这一位置可以被其他原子或离子占据
Coordination Number of Simple Cubic #
$$CoordinationNumberSimpleCubic=8$$
The Size of Interstitial Sites #
- 就Interstitial Site来说,其具有实际大小
- 前面Rock Salt中提到过Cations will always touch their nearest neighbour anions
- 阳离子总是会接触它们最近的阴离子,因此阳离子只有在足够大时才会占据晶体结构中的间隙位。如果阳离子太小,它将无法与最近的阴离子接触,因此不会稳定地占据间隙位
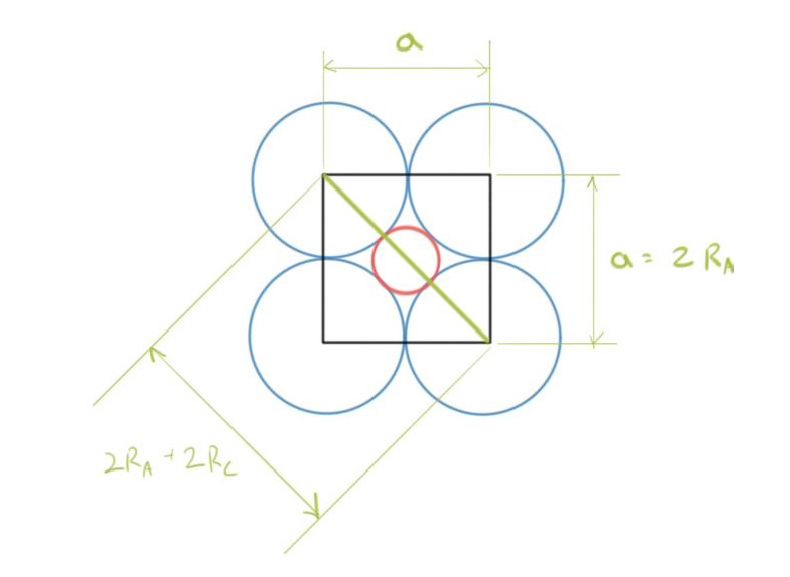
$$\sin 45 = \frac{2R_A}{2R_A + 2R_C} \
(2R_A + 2R_C)\sin 45 = 2R_A \
2R_A\sin 45 + 2R_C\sin 45 = 2R_A \
R_A\sin 45 + R_C\sin 45 = R_A \
\frac{R_A}{R_A}\sin 45 + \frac{R_C}{R_A}\sin 45 = 1 \
\sin 45 + \frac{R_C}{R_A}\sin 45 = 1 \
\frac{R_C}{R_A}\sin 45 = 1 - \sin 45 \
\frac{R_C}{R_A} = \frac{1 - \sin 45}{\sin 45}=0.414$$
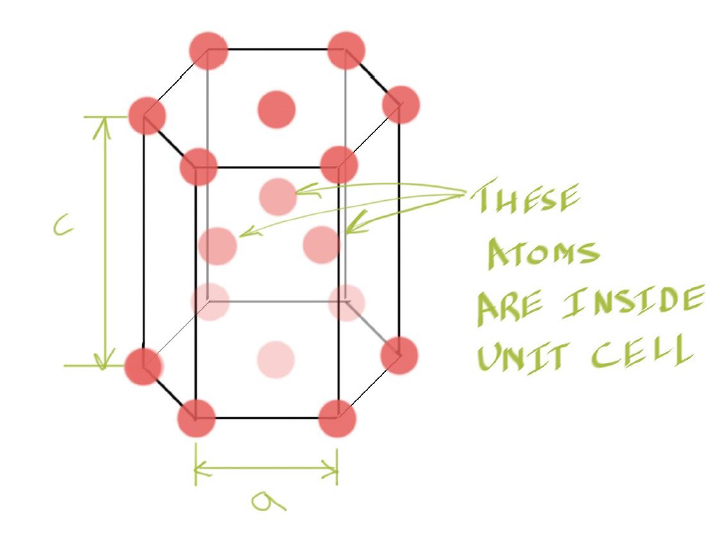
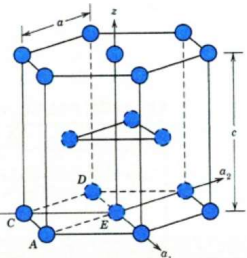
Hexagonal Close Packed (HCP) Structure #
- 结构特点:原子以六边形排列,沿c轴有堆叠的结构。原子层是按照ABAB…的顺序堆叠。
- n:每个晶胞含有 6 个原子(从整体堆叠考虑)。
- CN:12(类似于FCC,每个原子有12个最近邻原子)。
- APF:约 74%。
- ex.:镁、钛、锌等
Number of Atoms in HCP #
Coordination Number of HCP #
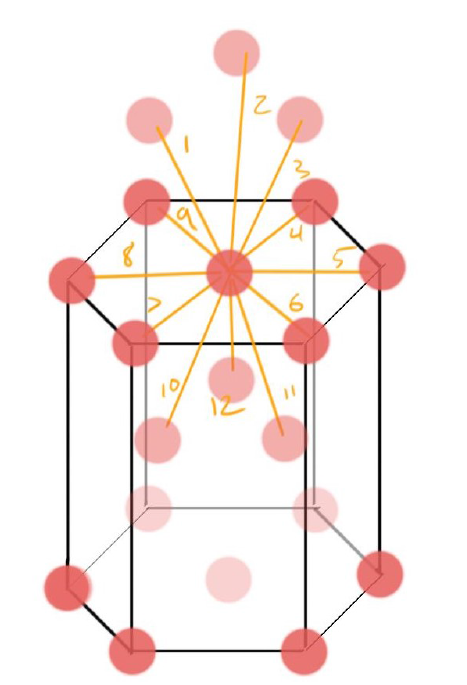
- CN = 12
Atomic Packing Factor in HCP #
- HCP有着和FCC一样的APF(都为0.74)所以FCC有时会被称为CCP
Different to FCC #
- FCC和HCP的主要区别在于原子的堆积顺序
- FCC中的原子堆积顺序是ABCABC
- 而HCP中的堆积顺序是ABAB
- 尽管它们的堆积顺序不同,但由于原子排列非常紧密,它们的APF都是0.74
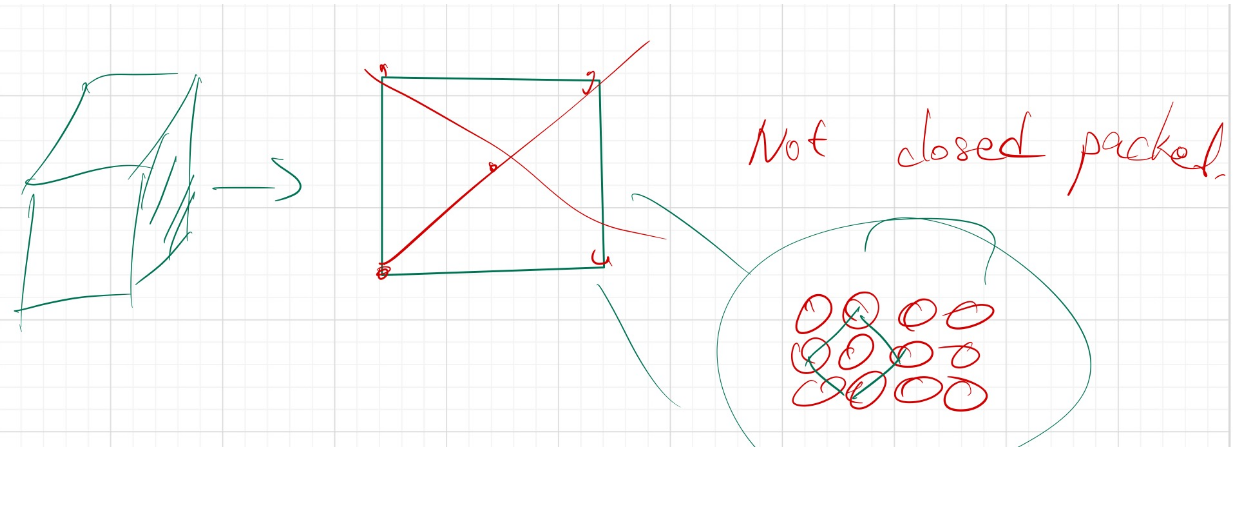
Close Packed #
- 要想让Atom排列的更加紧密,需要有Close Packed的结构
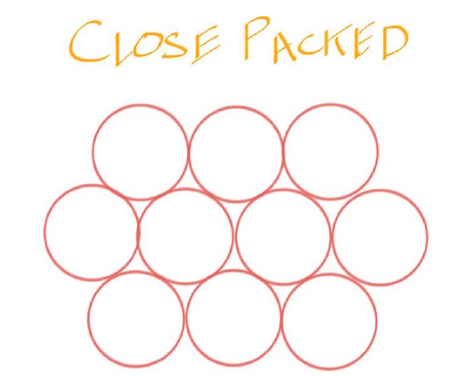
- 当Atom在这种排列下,APF才能更高
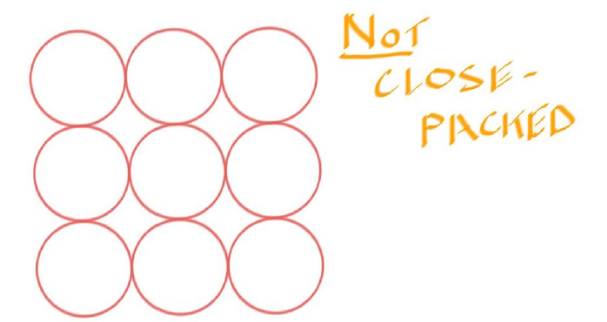
- 在Not Close Packed下,这种排列的方式更加的松散
Closed Packed Plane #
Not Closed Packed Plane in FCC #
- 对于FCC的侧面上的Atom来说,其并不处于Closed Packed状态下