EF9.ResistiveCircuits #
Last Edit: 3/3/25
Ohm’s Law #
- Ohm’s Law是以德国物理学家 Georg Simon Ohm 的名字命名的,他确立了 Voltage 和 Current 之间的关系,其发现了 Resistor 两端的 Voltage 和通过的 Current 成正比
Symbol for a Resistor #
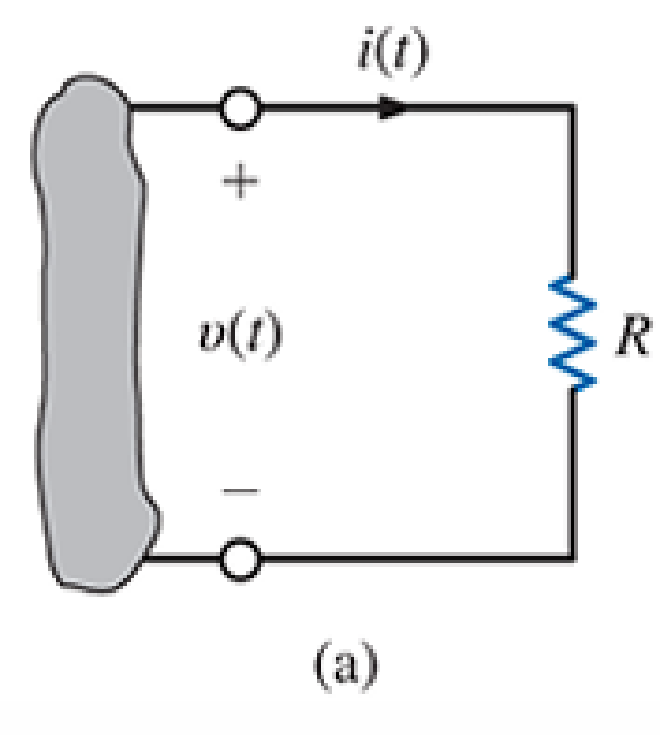
Mathematical Relationship #
- Ohm’s Law 指出
$$ v(t) = Ri(t), \text{ where } R \geq 0 $$
- 其中 Ohms 的符号为 \(\Omega,1\Omega=1V/A\)
Graphical representation of V vs. I #
- 不同用电器有着不同的 Voltage-Current Relationship
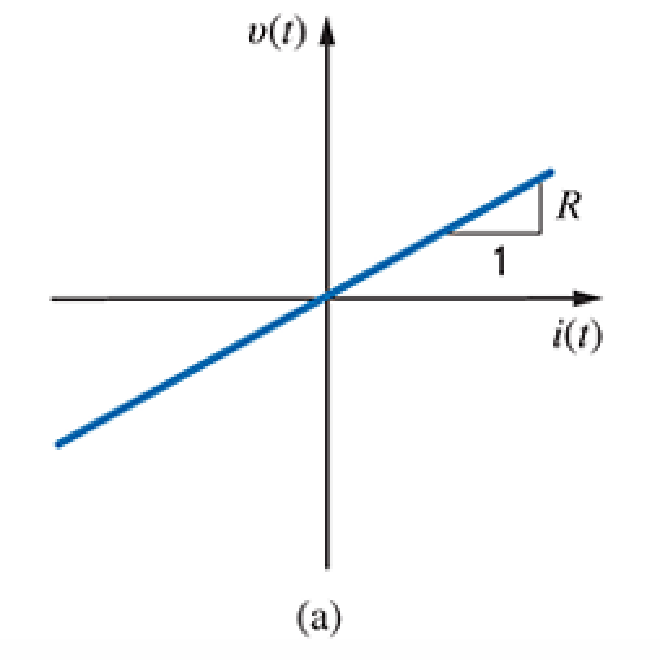
- 一个线性电阻器
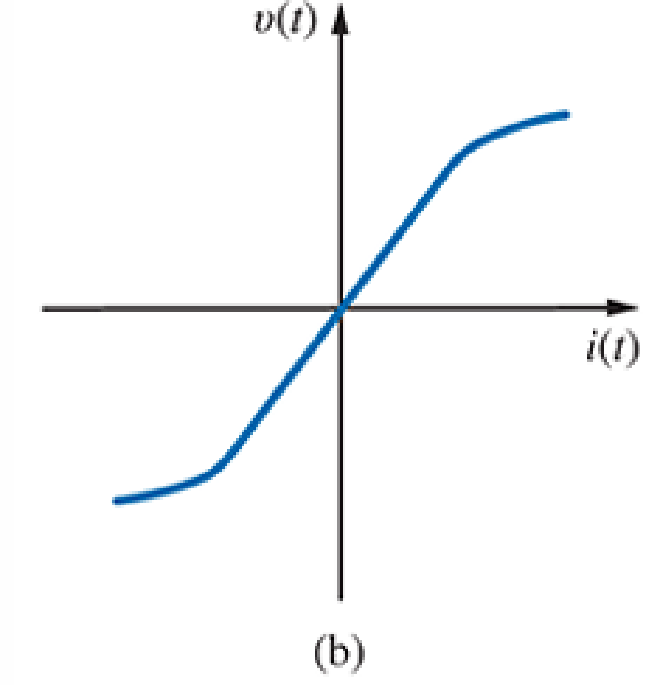
- 一个 Light Bulb 的则是非线性的关系
Conductance 电导 #
- Conductance 由符号 G 表示,其是 Resistor 的倒数
- 它的单位是 Siemens,有 \(1S=1A/V\)
Power Relationships #
- Power 的最基础的定义为 W = VI,也就是
$$ p(t) = v(t) i(t) $$
- 当把 \(V=Ri\) 带入,有
$$ p(t) = Ri^2(t) = \frac{v^2(t)}{R} $$
- 带入 Conductance \(i(t) = Gv(t)\) 可以得到
$$ p(t) = \frac{i^2(t)}{G} = Gv^2(t) $$
Conductor’s Influence in Circuit #
- 对于一个位于 Circuit 中的 Resistor 来说,其可以通过变换对 Circuit 整体造成不同的影响
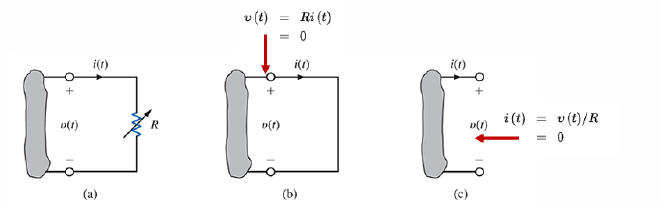
- 如上图所示,当 Resistor 减小到零的时候,电源两端直接连线,形成 Short Circuit
- 而到了 C 中,Resistor 增大到无限大时,形成 Open Circuit
Kirchhoff’s Laws #
- Kirchhoff’s Laws 具体表现为 Kirchhoff’s Current Law 和 Kirchhoff’s Voltage Law
KCL Current Law #
- 对于一个 Circuit 中的 Node 来说,其 Algebraic Sum of the Current leaving or entering a node is zero,说明从节点流出或流入的电流 之代数和为零
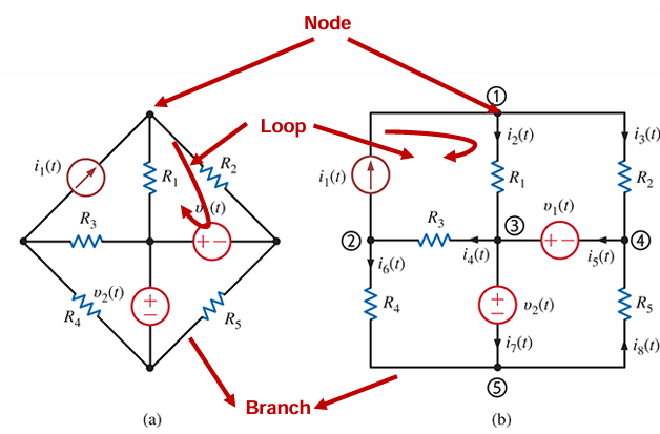
- 想要解决 Circuit 中每一个 Node 的 Current 的办法就是通过解线性方程组,而并不是每一个节点的 Equation 都在 System 中是 Linearly Independent 的,这说明仅需要选择线性独立的方程来进行分析
Kirchhoff’s Voltage Law #
- KVL 指出,在任何闭合回路中,电压的代数和必须为零
Voltage Division #
- 在 Series, Parallel Circuit 中,需要进一步通过 Current 和 Voltage 在不同情况下的性质在写出 Linear Equation 后进一步求解

- 当 Circuit 中存在一个 Series 的时候,可以得到d
$$ -v(t) + v_{R1} + v_{R2} = 0\Rightarrow v(t) = v_{R1} + v_{R2} $$
- 根据 Ohm’s Law 可以知道,\(v_{R1} = R_1i(t),v_{R2} = R_2i(t)\),有 \(v(t)=R_1i(t)+R_2i(t)\),可以解出 \(i(t) = \frac{v(t)}{R_1 + R_2}\)
- 带回 \(v_{R_1}=R_1 i(t)\) 后可以得到
$$ = R_1 \left[ \frac{v(t)}{R_1 + R_2} \right] = \frac{R_1}{R_1 + R_2} v(t) $$
Multiple-Source/Resistor Networks #
- 有的时候的 Circuit 会非常复杂,比如存在多个 Voltage Sources 的情况,这时候就需要通过 Simplified Equivalent Circuit 来分析 Circuit
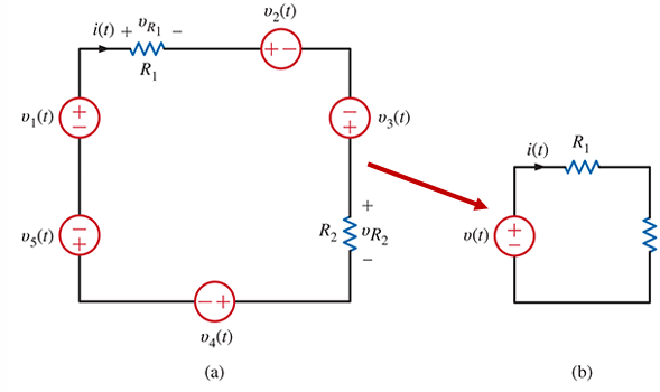
- 上图中,a 存在了多个 Voltage Sources 和 Resistors,沿着 Closed Loop 列出所有 KVL 方程 \(+vR1+v2(t)−v3(t)+vR2+v4(t)+v5(t)−v1(t)=0\),将所有非 Resistor 的 Voltage 移动到等式右边,有 \(vR1+vR2=v1(t)−v2(t)+v3(t)−v4(t)−v5(t)\)
- 根据 KVL ,就可以创建一个 \(R_S=R_1+R_2+R_3+R_4+R_5\) 的等效电路
- 于是就把整个 Circuit 化简为了 b 中的等效电路
ex. Find Voltage in a fragment #
有以下图 a,求 bd 段的等效电路
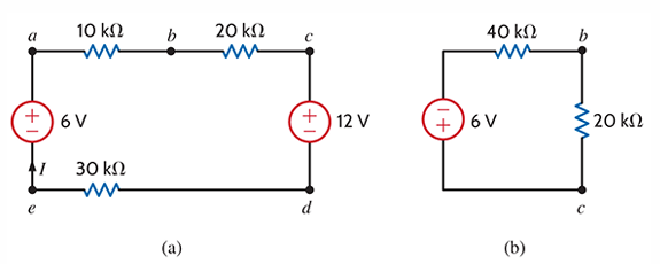
- 在同时存在 Resistor 和 Battery 的情况下,要先求得他们的 Current (串联分压不分流)
- 根据 KVL,有
$$ 10kI + 20kI + 12 + 30kI - 6 = 0\Rightarrow60kI = -6 \Rightarrow I = -0.1 , \text{mA} $$
- bd 段的 Voltage 自然可以通过 \(10kI + V_{bd} + 30kI - 6 = 0\) 得到,代入 \(I = -0.1 , \text{mA}\) 后得到 \(V_{bd}=10V\)
ex2. #
求出 \(V_S\) 段的 Voltage
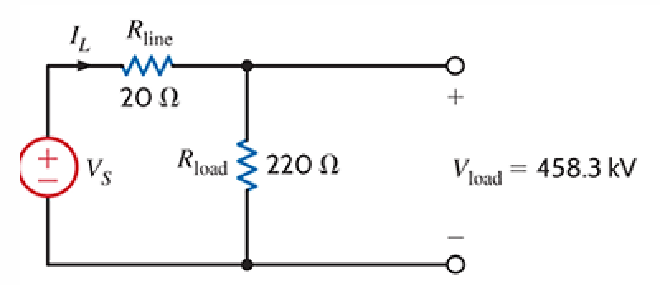
- 已知 Parallel Circuit 分流不分压,有 \(I_L=458.3/220=2.083~kA\)
- 后面又进入了一个 Series Circuit,有 \(V_{line}=20\cdot 2. 083=41.66 ~kV\)
- 根据 KVL,可以得到 \(V_S=V_{line}+V_{load}=500 ~kV\)
Single-Node-Pair Circuits #
- 串联分压,并联分流的原理也可以通过 KVL 进一步验证
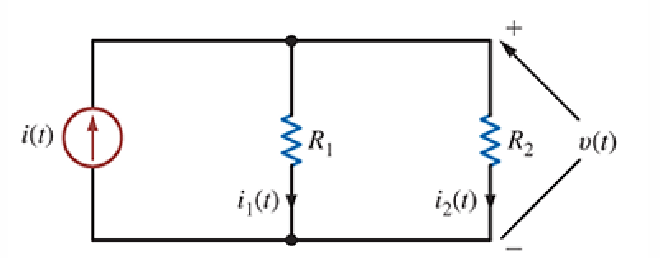
- 对于上面的电路,有
$$ i(t) = \frac{v(t)}{R_1} + \frac{v(t)}{R_2} = \left( \frac{1}{R_1} + \frac{1}{R_2} \right) v(t) = \frac{v(t)}{R_p} $$
- 能总结出公式为
$$ i_1(t) = \frac{v(t)}{R_1}\Rightarrow i_1(t) = \frac{R_2}{R_1 + R_2} i(t) $$
- 可以用于计算 Parallel Circuit 中的 Current
Multiple-Source/Resistor Networks #
- 对于具有 n 个 Parallel Resistor 的 Circuit,根据 KVL 可以得出
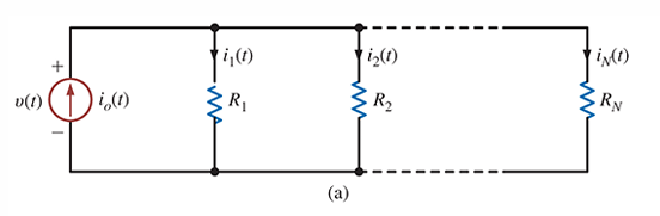
$$ i_0(t) = i_1(t) + i_2(t) + \ldots + i_N(t) = \left( \frac{1}{R_1} + \frac{1}{R_2} + \ldots + \frac{1}{R_N} \right) v(t) $$
- 其中每一个 Parallel Circuit 上的 Resistor 可以通过
$$ i_j(t) = \frac{v(t)}{R_j} \quad \quad i_j(t) = \frac{R_p}{R_j} i_o(t) $$
- 得出答案