Last Edit: 2/20/25
Faraday’s Law of Induction #
- 任何封闭电路中 Induced Current 大小,等于穿过这一电路 Magnetic Flux 的变化率
- 已知 Magnetic Flux 的定义即为 \(\Phi_B=\int B\cdot dA\)
Experiment on change of Magnetic Flux #
- 如图所示,现在有两个独立闭合电路
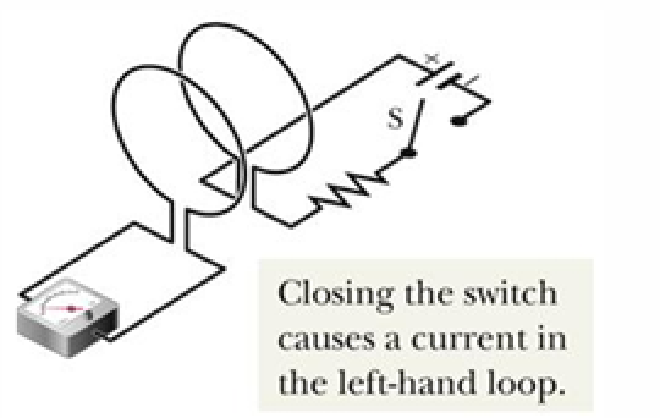
- 当开关 S 闭合后,右侧电路会生成一个 Magnetic Field,此时左侧度数瞬间有读数后消失,这表明了 Change in Magnetic Flux caused the Induced Charge in the left loop
EMF Electromotive Force #
- EMF 实际上被叫做 Electromotive Force,即电动势,虽然名字中有 Force,但其实际上是 Potenial Difference,单位是 Volt
- 在 Faraday’s Law 中,emf 由 Induced Charge 引起
EMF 来自来源于早期的电学研究,当时科学家认为电池、电机等装置“推动”电荷,所以称之为“电动势”,尽管它的单位和电压一样(伏特, V),但两者有一些区别
- Faraday’s Law 给出 EMF 的数学表达为 $$\mathcal{E} = -\frac{d\Phi_B}{dt}$$
- \(\mathcal{E}\) 是 EMF
- \(\Phi_B\) 是 Magnetic Flux
- t 是时间
- 负号(来自Lenz’s Law)表示感应电流方向总是抵抗磁通量的变化
- 也就是说当磁通量随时间变化时,就会在回路中产生 EMF,推动电荷流动,从而形成Induced Charge
Coil #
- 当存在多匝线圈的时候,Total EMF 为 $$\mathcal{E} =−N\frac{dΦB}{dt}$$
Ways of changing Magnetic Flux #
- 已知 \(ΦB=BAcosθ\),可以知道想要改变 Magentic Flux,可以改变 Magnitude of Magnetic Flux,Area of Coil & Angle Between A & B
Lenz’s Law #
- After Faraday propsed his law of induction, Heinrich Friedrich Lenz devised a rule for determinging the direction of an induced current in a loop
- 楞次定律描述了感应电流的方向,它的核心思想是 Induced Current 会产生一个 Magnetic Field 来抵抗 Magnetic Flux 的变化
- 换句话说,线圈中的 Induced Current 会尽可能 Resisit Magnetic Flux 的增加或减少
*如果磁通量增加,感应电流会产生一个相反方向的磁场来抵抗增加 如果磁通量减少,感应电流会产生一个相同方向的磁场来补偿减少
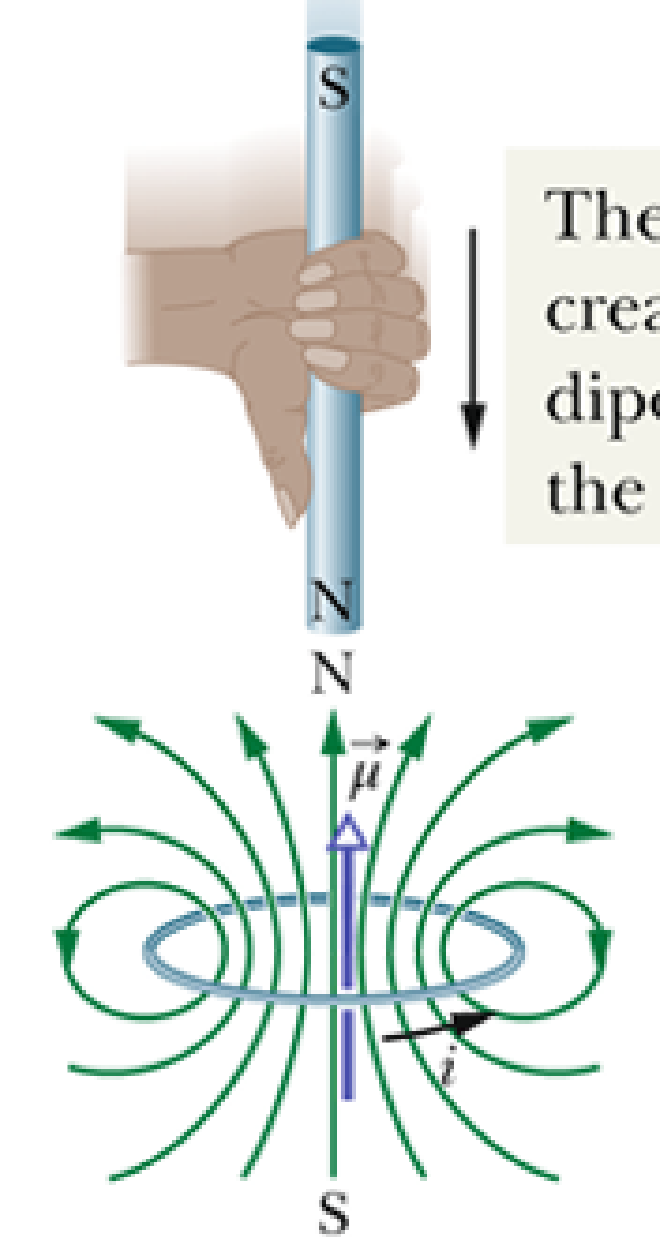
- 当 Magnet 靠近 Coil 时,Magnetic Flux 增加,Coil 会产生一个向北的 Magentic Field 以抵抗 Change in Magnetic Flux,通过 Right Hand Rule 就可以确定这一 Magnetic Field 是由 CCW 方向的 Induced Current 形成的
Induction and Energy Transfers #
- 现在有以下场景,一个闭合的导体电路在一个 Uniform Magnetic Field 中被拉出
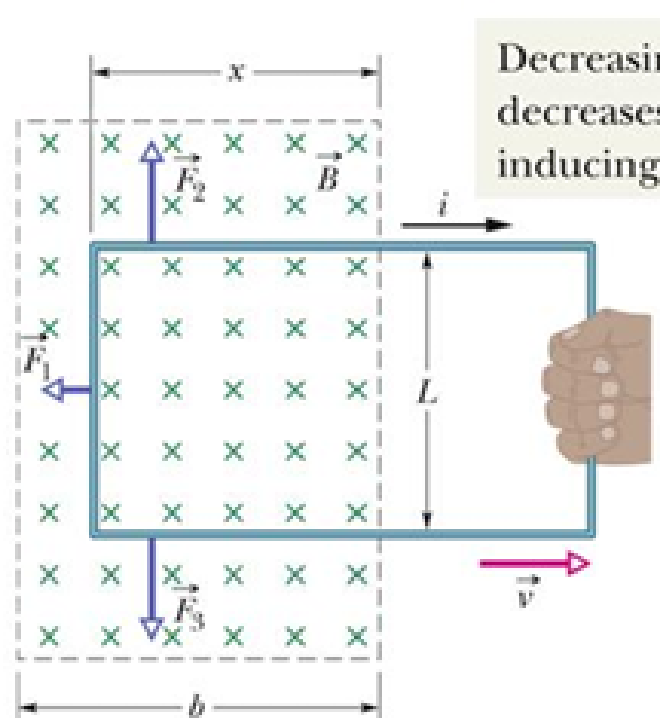
- 这一运动的结果是,Magnetic Flux 减少
- 根据 Faraday’s Law,回路中产生 Induced Current
- 根据 Lenz’s Law,Induced Current 方向会抵抗磁通量的减少,形成 CW
- 前面没有提到的是,这一个过程必然会产生一个 Force,即拉动线圈的过程中,EMF 会产生一个和拉动方向相反的 Force,而这一个 Force 于 Velocity 平行,有 \(P=Fv\),这一做功将最终转换成 Induced Current 中的 Electric Energy,即能量守恒
Induced EMF #
- 已知 \(\mathcal{E} = -\frac{d\Phi_B}{dt}\),由于上面的回路在 Magnetic Field 中被拉出,Magnetic Flux 的变化为 $$\mathcal{E}=BLv$$
Induced Current #
- 根据 Ohm’s Law, $$i=\frac{\mathcal{E}}{R}=\frac{BLv}{R}$$
Opposing Force #
- 根据洛伦兹力作用,有 $$F=iLB=\frac{B^2L^2v}{R}$$
Rate of Work #
- 与上方同理,外力做功为 $$P=Fv=\frac{B^2L^2v^2}{R}$$
Thermal Energy Dissipation #
- Current 在 Resistor 中流动的时候,一部分 Energy 会损耗为 Thermal Energy,有 $$P=i^2R=(\frac{BLv}{R})^2R=\frac{B^2L^2v^2}{R}$$
ex. Comparison of EMF #
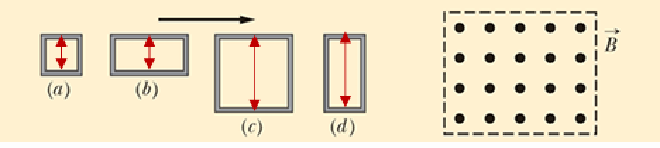
- 现在有四个 Wire Loop,依次要穿过 Magnetic Field,要求比较 EMF 大小,已知 Faraday’s Law \(\mathcal{E} =BLv\),只有垂直于运动方向的边长才决定 Induced EMF 大小,有
- (a)\(\mathcal{E} = B L v\)
- (b)\(\mathcal{E} = B L v\)
- (c)\(\mathcal{E} = B (2L) v\)
- (d)\(\mathcal{E} = B (2L) v\)
Eddy Currents #
- Eddy 涡流是闭合导体在变化的磁场中产生的环形感应电流,类似于水中的漩涡
- 假设我们用 Conductor Board 代替之前的闭合导体回路
- 由于磁通量变化,根据 Faraday’s Law,导体中会产生 Induced Current
- 但由于导体是连续的金属板,电流不会沿着单一路径流动,而是形成 Eddy Current
- 这些感应电流与磁场相互作用,产生反作用力,阻碍导体的运动
Inductors and Inductance #
- Capacitor 用于产生所需的 Electric Field,而 Inductor 用于产生所需的 Magnetic Field
- Solenoid 是最基本的电感器,当电流 i 通过其线圈时,产生磁通量 ΦB
- Inductor L 通过磁通量 \(\Phi_B\) 定义为: $$L = \frac{N \Phi_B}{i}$$
- N 是线圈的匝数
- \(\Phi_B\) 是磁通量
- i 是电流
- Inductor 的单位是亨利(Henry, H)
- 1 亨利的定义: \(1 H = 1 T \cdot m^2 / A\)
- 如果1 安培电流变化 1 秒,导致1 伏特感应电动势(EMF),则电感值为 1 亨利
- 对于 Solenoid,其单位长度的电感为: $$\frac{L}{l} = \mu_0 n^2 A$$
- \(\mu_0\) 是真空磁导率(\(4\pi \times 10^{-7} H/m\))
- n 是每单位长度的匝数(匝数密度)
- A 是螺线管的横截面积
Property of Inductance #
- 电感 L 仅取决于电感器的几何结构(类似于电容器的电容取决于板间距离和面积)
- 线圈匝数的平方关系
- 若匝数增加 n 倍,则:
- 磁通量 \(\Phi_B\) 增加 n 倍(因为磁场 B 增加)
- 电感 L 增加 \(n^2\) 倍,因为磁通量和线圈匝数同时增加
Self-Induction #
- 就像是一个具有 Mass 的物体存在惯性,抵抗瞬间产生的加速度一样,当 Current 在快速变化的时候,Inductor 会通过 Induced EMF 进行反抗
- 也就是说当 Current 变化的时候,Inductor 根据公式 \(\mathcal{E} =−L\frac{di}{dt}\) 产生一个 Induced Current Opposing the change 来 “缓冲” 这一变化
Energy Stored in a Magnetic Field #
- Inductor 在 Current 流过时会储存能量,该能量由磁场存储,并由以下公式计算 $$U_B=\frac{1}{2}Li^2$$
- \(U_B\) 是存储的 Magnetic Energy(单位: J)
- L 是 Inductor(单位: H)
- i 是线圈中的 Current(单位: A)
电容器存储电场能量(\(\frac{1}{2} C V^2\)),电感器存储磁场能量(\(\frac{1}{2} L i^2\))