Last Edit: 2/6/25
Capacitor 电容器是一种储存 Electrical Energy 的装置,由两个相互隔离的导体(即极板)组成,分别带有 +q 和 -q 的电荷
5.1 Capacitance 电容 #
- Capacitance 电容代表了导体储存 Charge 的能力,表示一个电容器在一定的电压下能储存多少电荷,其基本定义是 $$q=CV$$
- 其中 \(V\) 是两个 Plate 极板之间的 Potential Difference
Charging a Capacitor #
- 要使 Capacitor 充电,需要利用到电池两侧初始存在的 Potential Difference
- 由于电池两侧存在 Potential Difference,于是就形成了一个 Electirc Field,电场会对电荷产生一个 Force \(F=qE\) ,这使得电荷在电场中受力,正电荷从负极电极到了正极(正电荷是不会移动的,只有负电荷会,这里的“移动”是假设”,负电核到了正极
- 举一个例子就是假设一开始电池具有 10 V 的电压,充电完成后正极板上有 +10V,负极则有 0V,此时由于两个电极板之间是绝缘的,电荷会积累到电极板表面并形成 Electric Field,从正极指向负极,此时电路中的电极板电压等于电池电压,电荷不在移动,电极板完成整个充电的过程
类比一个水流抽水的过程,电池就是水泵推动水在管道中移动
Property of Capacitance #
- 与电阻一样,电容是一个电容器的特性,其即使公式为 \(q=CV\) ,但实际上其并不依赖于储存的电荷量 q
- 真正影响电容的因素为形状,尺寸,相对位置以及介质
也就是说 q = CV 这个公式真正定义的是 q 和 V 之间的系数关系
5.2 Calculating The Capacitance #
不同类型的电容器,其电容值的计算方式不同,具体取决于几何结构和极板之间的介质
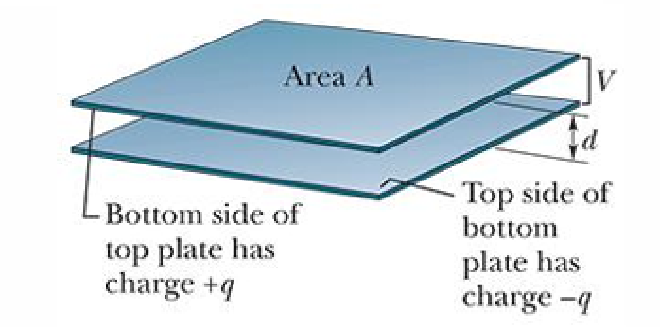
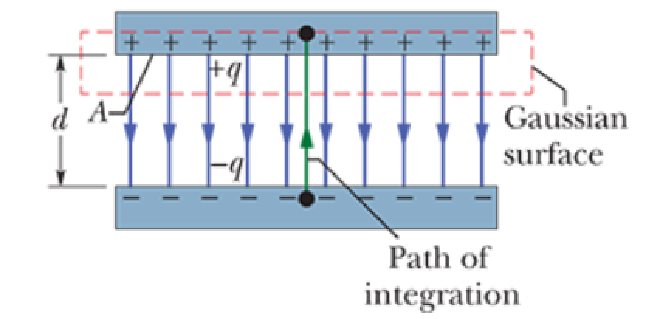
Parallel-Plate Capacitor 平行板电容器 #
-
当有两个面积为 A 的平行导体板相距为 d 的时候,其电容有 $$C=\frac{\varepsilon_0 A}{d}$$
-
可以看出面积增大、电极板距离减小时,电容增大
Cylindrical Capacitor 圆柱形电容器( #
- 两个同轴圆柱导体,内外圆柱的半径分别为 a 和 b,长度为 L $$C = 2 \pi \varepsilon_0 \frac{L}{\ln(b/a)}$$
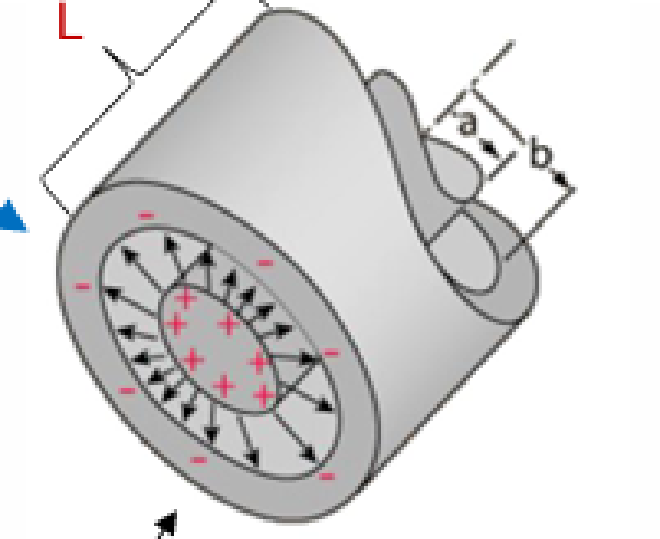
- 电容与圆柱长度 L 成正比,内外圆柱半径比值决定了电容大小。
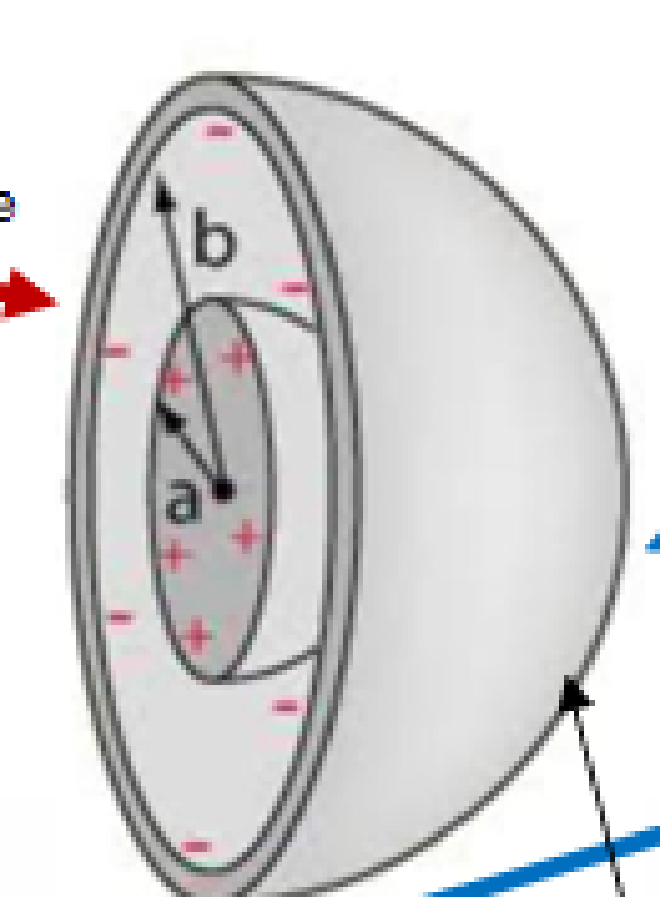
Spherical Capacitor 球形电容器 #
- 两个同心球形导体,内外球半径分别为 a 和 b
$$C = 4 \pi \varepsilon_0 \frac{ab}{b - a}$$
Isolated Spherical Capacitor 孤立球形电容器 #
- 仅有一个孤立的球体,半径为 R $$C = 4 \pi \varepsilon_0 R$$
- 孤立球体的电容只与球体半径有关
ex. Change in Capacitance when change in radius #
A drop of mercury is an isolated sphere with radius R= 3.83. What is the capacitance of a drop that results from three drops of mercury combined, each with the same radius R
- 三个球的总体积为: $$V_{\text{total}} = 3 \times \frac{4}{3} \pi R^3 = 4 \pi R^3$$
- 此时可以求出新半径 \(R’ = \sqrt[3]{3} R = 1.442 , R\)
- 将 R=3.83R = 3.83 代入: $$R’ = 1.442 \times 3.83 \approx 5.524$$
- 已知孤立球体的电容公式为: $$C = 4 \pi \varepsilon_0 R$$
- 带入半径之后得到 $$C≈6.14×10−10 FC \approx 6.14 \times 10^{-10} , \text{F}$$
5.3 Capacitors in parallel and in series #
- 电路中的电容器也将遵循并联和串联的特性
5.3.1 Capacitors in Parallel #
- 对于一个电路,其中三个 Capacitors 并联放置,有 $$\ q_1 = C_1 V, \ q_2 = C_2 V, \mbox{ and } \ q_3 = C_3 V$$
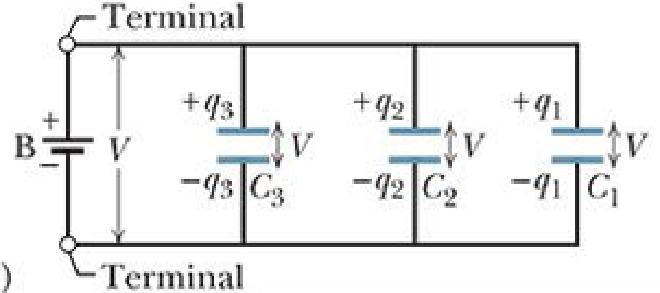
- 根据串联分压,并联分流的特性,说明并联的时候每个电容器 V 相等,有 $$q = q_1 + q_2 + q_3 = (C_1 + C_2 + C_3) V$$ $$C_{eq} = \frac{q}{V} = C_1 + C_2 + C_3$$
- 也就是说电容器并联时,总电容 \(C_{\text{eq}}\) 增大
5.3.2 Capacitors in Series #
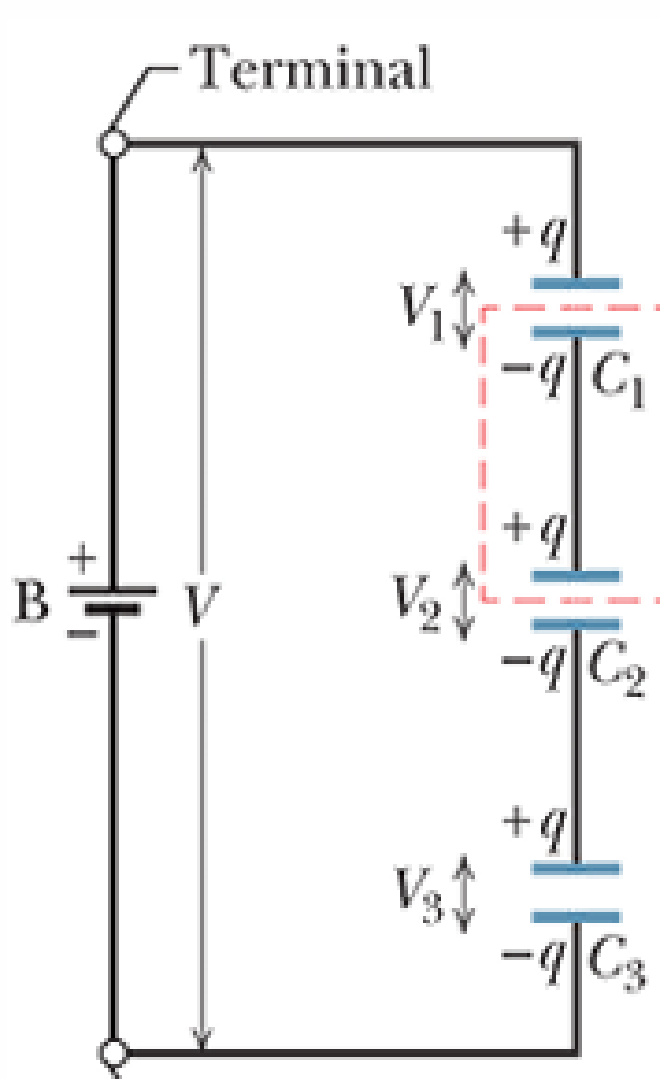
- 到了串联的时候,每个电容器电流相同,也就是 q 一致,有
$$V_1 = \frac{q}{C_1}, \quad V_2 = \frac{q}{C_2}, \text{ and } \quad V_3 = \frac{q}{C_3}$$
ex. Capacitors in both Parallel and Series #
Find charge on C1

- 首先计算 C1 和 C2 两个 Parallel Capacitor 的总电容,有并联电路 $$C=C_1+C_2=17.3$$
- 之后这个 17.3 再和 4.5 串联,有 $$\frac1C=\frac{1}{17.3}+\frac{1}{4.5}\Rightarrow C=3.57$$
5.4 Energy Stored in an Electric Field #
当外部装置(如电池)对电容器充电时,做的功以势能 U 的形式储存,有 $$U=\frac{q^2}{2C}$$
- 当带入 \(q =cv\) 的时候,得到另一种形式 $$U=\frac 12CV^2$$
- 做的功主要是由 Electric Field Strength \(F=qE\) 提供,具体来说是将负电荷从一个极板移动到另外一个极板所做的功,完整推导如下
- 当少量电荷 dq 从一个极板到达另一个的时候,两个极板之间形成一个初始电场 E,导致极板之间产生 Potential Difference \(V=\frac qC\)
- 想要在移动电荷,则需要 Electric Field Strength,F 做功,有 \(W=Fd\),其中 F就是电场力,那么就有 \(dW= Fdl\),用了 l 替换 d,同时因为 \(F=qE\),有 \(dW=qE\cdot dl\)
- 现在知道电势差 V 与电场的关系为 $$V=-\int^b_a\vec E\cdot dl$$
积分在均匀电场和点电荷电场等对称电场中简化,有 \(V_{AB} = - \int_A^B \vec{E} \cdot d\vec{l} = - E \int_A^B \cos \theta , dl\),\(V_{AB} = - \int_A^B \frac{kq}{r^2} , dr = kq \left( \frac{1}{r_A} - \frac{1}{r_B} \right)\) 等
- 从上面的 V 中可以推导出 \(dV=-E \cdot dl\),带回做功的公式中有 \(dW=q\cdot dv\),观察此时的公式,它描述的是一个电荷在经过路径上不同的 V 的时候产生的功,也就是一个电荷在不同电势的路径下的功
- 而我们像描述的是一个充电,也就是电荷累加到极板上的一个过程,此时的瞬时电势 V 将会是一个 Constant,但是电容器极板上的 Charge 则会随时间增加,即每增加一个微小的电荷 dq,电场力都要做一个微小功为 \(dW=V\cdot dq\)
- 两边积分得到 $$W=U=\int^Q_0 V\cdot dq=\int^Q_0\frac{q}{C}\cdot dq=\frac{q^2}{2C}$$
为什么 W = U 我也不知道
Distance between plates and Capacitance #
- 已知\(U = \frac{q^2}{2C}\) ,将 \(C = \frac{\varepsilon_0 A}{d}\) 带入,有 \(U = \frac{q^2}{2 \frac{\varepsilon_0 A}{d}}\),整理得到 $$U = \frac{dq^2}{2 \varepsilon_0 A}$$
Energy Density #
- 能量密度由总能量除以体积得到,有 $$u = \frac{U}{Ad} = \frac{CV^2}{2Ad}$$
- 带入 \(C = \frac{\varepsilon_0 A}{d}\) 得到 $$u = \frac{1}{2} \varepsilon_0 \left( \frac{V}{d} \right)^2= \frac{1}{2} \varepsilon_0 E^2$$
Dielectric #
- 介电材料是绝缘的材料,其填充在电容器板之间提高电容
- Michael Faraday 于1837年发现了此规律,并且定义加入介电材料后的电容值将会增加一个比例因子 \(\kappa\) ,其中真空中的介电常数默认为 1
Breakdown Potential #
- 在电容器中加入了介电材料后,这个材料会存在一个 Maximum Potential (Breakdown Potentioal),当电压超过这个值,Dielectirc 会被 Break Down 击穿并变为导体
| Material | Dielectric Constant ( \kappa ) | Dielectric Strength (kV/mm) |
|---|---|---|
| Air (1 atm) | 1.00054 | 3 |
| Polystyrene | 2.6 | 24 |
| Paper | 3.5 | 16 |
| Transformer oil | 4.5 | |
| Pyrex | 4.7 | 14 |
| Ruby mica | 5.4 | |
| Porcelain | 6.5 | |
| Silicon | 12 | |
| Germanium | 16 | |
| Ethanol | 25 | |
| Water (20°C) | 80.4 | |
| Water (25°C) | 78.5 | |
| Titania ceramic | 130 | |
| Strontium titanate | 310 | 8 |
For a vacuum, ( \(\kappa = 1\) ).*
Capacitor with a Dielectric #
- 当加入了 Dielectric 后,电容公式改变为 $$C = \kappa \frac{\varepsilon_0 A}{d}$$
- 同时可以定义一个 \(l=\frac{A}{d}\),公式就变为 \(C = \kappa \varepsilon_0 \ell\)
- 电压 V 保持恒定(并联电容器)**: $$q = CV = \kappa \varepsilon_0 \ell V$$
- 电荷 q 保持恒定(串联电容器) $$V = \frac{q}{C} = \frac{q}{\kappa \varepsilon_0 \ell}$$
Super Capacitor #
对比了超级电容器(Supercapacitor)与锂离子电池(Lithium-ion battery)的性能和特性:
| 功能 | 超级电容器 | 锂离子电池(通用) |
|---|---|---|
| 充电时间 | 1 – 10 秒 | 10 – 60 分钟 |
| 循环寿命 | 100 万次或 30,000 小时 | 500 次及以上 |
| 单元电压 | 2.3 至 2.75 伏 | 3.6 至 3.7 伏 |
| 比能量 (Wh/kg) | 5(典型值) | 100 – 200 |
| 比功率 (W/kg) | 高达 10,000 | 1000 – 3000 |
| 每 Wh 成本 | 约 20 美元 | 0.50 – 1.00 美元(大系统) |
- 超级电容器充电快、循环寿命长、比功率高,但能量密度低,成本较高
- 锂离子电池有较高的能量密度和较低的成本,但充电时间长,循环寿命较短
ex. Energy change when insert an Dielectirc #
- 平行板电容器的电容为 \(C = 13.5 , \text{pF}\),通过电池充电到电压 \(V = 12.5 , \text{V}\)
- 断开电池后,插入介电常数 \(\kappa = 6.50\) 的瓷板。
- 问题:
a) 插入前的电容器电势能是多少?
b) 插入后的电容器电势能是多少? - 插入前的电势能 \(U_i\) 为 \(U_i = \frac{1}{2} C V^2\) $$U_i = \frac{1}{2} \times 13.5 \times 10^{-12} , \text{F} \times (12.5 , \text{V})^2 = 1.055 \times 10^{-9} , \text{J} \approx 1100 , \text{pJ}$$
- 插入后的电势能 \(U_f\) $$U_f = \frac{q^2}{2 \kappa C} = \frac{U_i}{\kappa}$$ 插入介电材料后,能量减少,损失的能量为: $$W = U_i - U_f = 1055 , \text{pJ} - 162 , \text{pJ} = 893 , \text{pJ}$$
- 插入介电材料后,电势能因介电常数 \(\kappa\) 的影响减少。
- 损失的能量可被视为在插入过程中施加的机械功。