Last Edit: 1/23/25
4.1 Electric Potential #
- 对于一个重力场,其Field Strength为g,而Gravity所做的功则为\(W=mgh\)
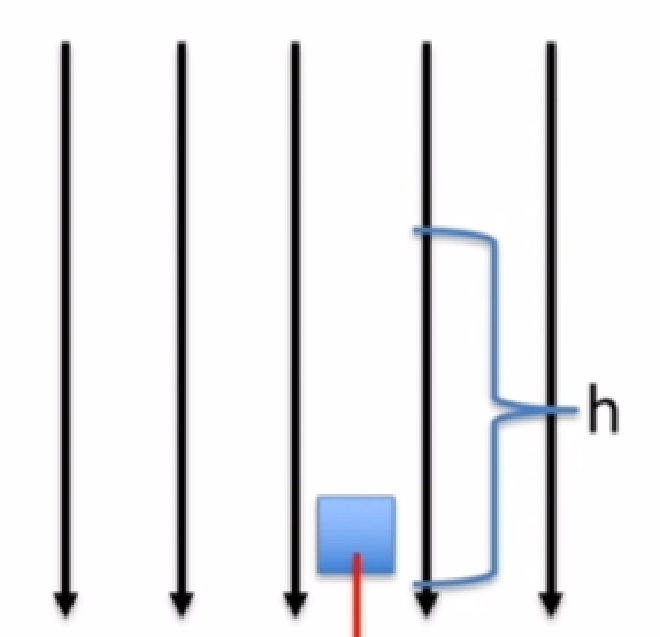
- 可以发现这一个Work Done只和高度差有关,与路径无关(也就是说即使在途中左右摇摆,重力做的功依然不变)
- 同理可以类比到Electric Field中,电场力做功为\(W=Eqh\),并且同样的与路径无关
Electrical Potential Energy 电势能 #
- Electrical Potential Energy 是带电粒子由于其位置处于电场中而具有的能量
- 如果Charge在Electric Field中做了Negative的Work,其就是在Electric Field中积累了Electric Potential Energy,于是就有公式 $$U=-W$$
- 其中U就是Electric Potential Energy 电势能
- 具体来说定义Electric Potential Energy的办法就是通过Test Charge的两个参考点,一个是无穷远处电荷之间相互作用力忽略不记的地方,到另一个参考点,Test Charge在这两个点之间做的功便为电势能
Electrical Potential 电势 #
- Electrical Potential 指的是电场中某一点单位电荷所具有的电势能 $$V=\frac{U}{q}$$
- 当Paritical从Electrical Field中的初始点移动到终点时,电势发生变化,用公式表示为 $$\Delta V = V_f - V_i$$
- 电势能的变化可以用公式计算,由于Paritcal的Charge并不发生改变,有 $$\Delta U = -W=q \Delta V = q(V_f - V_i)$$
- 在这一过程中,总能量是守恒的,这意味着动能和势能之和保持不变
- 从初始点 i 移动到终点 f 时,机械能守恒关系表示为: $$U_i + K_i = U_f + K_f 或\Delta K = -\Delta U$$
4.2 Equipotential Surfaces 等势面 #
- Equipotential Surfaces 指的是一个Electrical Potential 相等的区域,Partical沿着这一个Surface移动的时候不需要做功
Calculating the Potential from the Field #
- 根据Electric Field Magnitude可以计算出Partical移动后的Potential Difference
- 由于Partical在Electric Field中需要克服电场力做功,则有 $$dW=\vec E \cdot d\vec s\Rightarrow \int dW= V_f - V_i = -\int_i^f \vec{E} \cdot d\vec{s}$$
4.3 Electrical Potential Due to a Charged Particle #
- Charged Particle在空间中会形成一个Electrical Field,\(\vec{E} = \frac{1}{4\pi \epsilon_0} \frac{q}{r^2} \hat{r}\),将其代入积分 $$V = -\int_\infty^r \frac{1}{4\pi \epsilon_0} \frac{q}{r^2} dr= \frac{1}{4\pi \epsilon_0} \frac{q}{r}$$
A positively charged particle produces a positive electric potential. A negatively charged particle produces a negative electric potential.
ex. Rank the Electral Potential #
Assume all dots are Protons
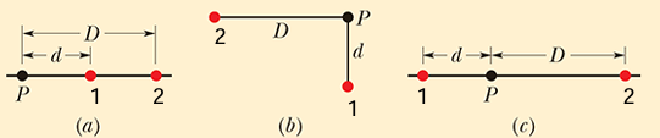
- 根据\(V= \frac{1}{4\pi \epsilon_0} \frac{q}{r}\),r越小V越大,有
- a) Proton 1 has more Electric Potential (v) than Proton 2, since D > d
- b) Proton 1 has more Electric Potential (v) than Proton 2, since D > d
- c) Proton 1 has more Electric Potential (v) than Proton 2, since D > d
4.7 Electrical Potential Energy of a system of charged Particles #
- 对于空间中的两个Particle,他们之间的距离为 r ,则由他们之间的Electrical Field相互作用而具有的Energy被称为他们的Potential Energy,前面已经提到了一个Partical在空间中会形成一个Electrial Potential \(V = \frac{1}{4\pi \epsilon_0} \frac{q}{r}\) ,而U是Partical在电场中所具有的能量,就有 $$U = \frac{1}{4\pi \epsilon_0} \frac{q_1 q_2}{r}$$
- U:两电荷之间的Electrical Potential Energy
- \(q_1、q_2\):两个电荷的电荷量(C)
- \(r\):两电荷之间的距离
- \(\varepsilon_0\):真空介电常数(\(8.85 \times 10^{-12} , \text{F/m}\))
Sign Convention #
- 已知2个Partical可能出现三种不同的系统
- 如果两电荷都是正电荷,它们会排斥,电势能 U>0
- 如果两电荷都是负电荷,它们同样会排斥,但电势能公式保持不变,因为两个负电荷相乘仍为正数,因此 U>0
- 如果两个电荷符号不同(例如,一个是正电荷,另一个是负电荷),它们会吸引,表示系统释放能量
ex. Potential Energy of a system of three charged particles #
有一个等边三角形的电荷系统,包含三个带电粒子:q1=+q,q2=−4q,q3=+2q,分别间隔12cm,求这个系统的Total Potential Energy
- 已知两个电荷之间的电势能为: \(U_{ij} = \frac{1}{4\pi \epsilon_0} \frac{q_i q_j}{d}\),总电势能是所有电荷对之间电势能的总和: \(U = U_{12} + U_{13} + U_{23}\) $$U = U_{12} + U_{13} + U_{23}$$ $$U = -\frac{4q^2}{4\pi \epsilon_0 d} + \frac{2q^2}{4\pi \epsilon_0 d} - \frac{8q^2}{4\pi \epsilon_0 d} $$ $$U = -\frac{10q^2}{4\pi \epsilon_0 d}$$
- 代入数据后可以得到 $$U = -\frac{10 (150 \times 10^{-9})^2}{4\pi \epsilon_0 \times 0.12}\Rightarrow U = -1.7 , \text{J} = -1.7 , \text{mJ}$$
负电势能意味着这个带电系统更稳定,或者说如果你想把这些电荷分开到无限远,就需要额外做功才能克服它们之间的相互作用。负值越大,系统的束缚越强。