Last Edit: 3/7/25
Node Analysis #
- 在 Kirchhoff’s Voltage Law, KVL 中,规定了在一个完整的 Closed loop 中,所有 Voltage rises 和Voltage drops 的代数和必须等于零
- 这是因为电压是势能差,一个完整的回路回到起点后,总能量变化应该为零,这是电荷守恒和能量守恒的直接体现
- 然而,对于 Partial path 或 Non-closed segment 非闭合段,其电压之和不一定为零,而是等于这些局部路径两端 Node 的电压差
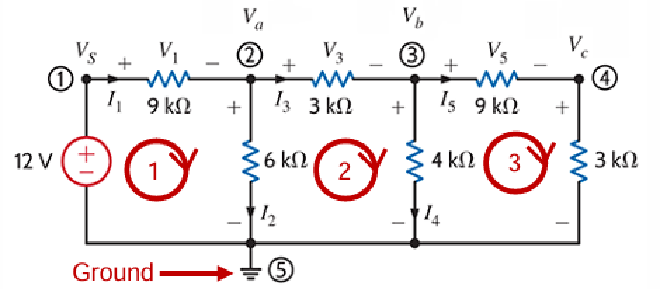
- 以上图为例,在 Node 1 到 2 之间,Potential Difference 为 \(V_s=V_1+V_a\)
- 而需要注意的是,在 Node Analysis 中,由 Battery 提供的初始 Voltage 被视为负值,有 \(-V_s+V_1+V_a=0\)
- 这是因为,当电路闭合的时候,Battery 推动 Electron 从负极向正极移动,并且在到达正极的时候获取了最高的 Electric Potential,之后在通过 Resistor 和其他负载的时候,Electron 会消耗这些 Potential Energy 以克服阻力,这视为 Potential 的下降
- 但是规定的符号与能量变换相反,即 Battery 提供 Electric Potential 的过程视为负号,用电器小号 Potential 的过程视为正号
- 总结上图中的 \(V_1,V_3,V_5\),可以得出
$$ I_1 = \frac{V_1}{9k} = \frac{V_s - V_a}{9k},I_3 = \frac{V_3}{3k} = \frac{V_a - V_b}{3k},I_5 = \frac{V_5}{9k} = \frac{V_b - V_c}{9k} $$
- 对于 \(6k\Omega\) 和 \(4k\Omega\) 来说,由于 Ground 是电路中所有 Node Potential 的参考零点,所以其本身为 0 V,也就是说 \(0=V_a-V_{6k\Omega}\),而它所对应的 Current 也就是
$$ I_2=\frac{V_{6k\Omega}}{6k}=\frac{V_a-0}{6k} $$
PD & Current Direction #
- 现在有以下 Circuit

- Voltage 即 Potential Difference 是一个参考量,即根据参考点的不同具有不同的数据,图中的 4 V 和 -2 V 即为相较于 Ground 也就是 0 V 参考的
- 而 Current 的 Direction 又和 Fragment 两端的 Node 的 Potential Difference 有关,呈现出的规律为 Current Will flow from higher to lower potential
- 在这张图中即为,R1 从上往下,R2 从左往右,R3 从下往上
Circuits containing only Independent Current Sources #
- 在没有 Voltage Source 而是 Current Source 的时候,Circuit 的行为主要由 Current Source 驱动,而不是 Voltage Source

- 上图中即存在两个 Current Source,\(i_A\) 和 \(i_B\)
- 而对于 Node 来说,Node 1 根据 KCL 有 \(i_A=i_1+i_2\),Node 2 有 \(i_2=i_B+i_3\)
- 现在进一步假设 \(I_A = 1,mA, R_1 = 12,k\Omega, R_2 = 6,k\Omega, I_B = 4,mA, R_3 = 6,k\Omega\)
- 已知 \({i}_1 = \frac{v_1}{R_1},{i}_2 = \frac{v_1 - v_2}{R_2},{i}_3 = \frac{v_2}{R_3}\),将他们带入原来的 Equation 中,有
$$ i_A = \frac{v_1}{R_1} + \frac{v_1 - v_2}{R_2},i_B = \frac{v_1 - v_2}{R_2} + \frac{v_2}{R_3} $$
- 带入数据得到
$$ 1\times 10^3=\frac{v_1}{12k}+\frac{v_1-v_2}{6k},-4\times10^3=\frac{v_1-v_2}{6k}=\frac{v_2}{6k} $$
- 解方程组后可以得到 \(V_1=-6V,V_2=-15V\),也就可以对应解出 \(I_1,I_2\) 了
同时也可以发现,如果一个 Circuit 中有 N 个 Node,则对应存在 N-1 个 Equation 需要解