Last Edit: 3/21/25
Coulomb’s Law 库仑定律 #
- 电荷之间相互作用力遵循的公式
- Coulomb’s Law 描述了两个 Charged Partials 之间的 Electrostatic Force(或Electric Force)
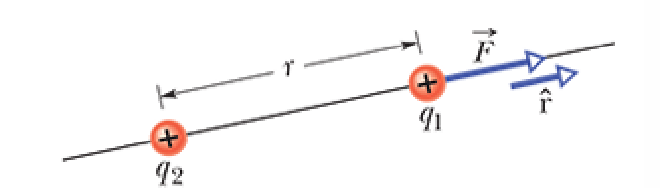
Electrostatic Force专指静止或相对静止的电荷之间的作用力 Electric Force则为更广义的术语,指电场对电荷施加的作用力
$$ F = \frac{1}{4 \pi \varepsilon_0} \frac{|q_1||q_2|}{r^2} \quad (\text{Coulomb’s law}) $$
- \(\varepsilon_0 = 8.85 \times 10^{-12} , \text{C}^2/\text{N} \cdot \text{m}^2\) Vacancies Permittivity Constant 真空介电常数
Permittivity Constant 体现了材料对电场的响应能力。真空介电常数是固定值,而不同材料的介电常数决定了其在电场中的行为特性
- \(\frac{1}{4πε0}=k = 8.99 \times 10^9 , \text{N} \cdot \text{m}^2/\text{C}^2\) 通常被 Electrostatic constant 静电常数 \(k\) 替代
- 由于两个Charged Particle之间的作用力是一条直线,所以其Electrostatic Force Vector 要么直接指向第二个Particle(相反的电荷符号),要么直接远离第二个粒子(相同的电荷符号)
- 如果多个 Electrostatic Force 作用在一个粒子上,则 Net Force 是各个力的 Vector Sum
ex. Electrostatic Force’s Net Force #
In the figure four particles form a square with edge length \(a = 3.64 × 10⁻²\) m. The charges are \(q₁ = q₄ = 1.77 × 10⁻¹⁵\) C and \(q₂ = q₃ = q\)
(a) What is q if the net electrostatic force on particle 1 is zero?

Shell Theorem 壳定理 #
Shell Theorem #1 #
- 对于一个带电粒子,如果它位于一个带电球壳的外部,且球壳的电荷均匀分布在表面上,该粒子受到的力等效于球壳的电荷全部集中在球壳的中心(即外部粒子感受到的电场与球壳的半径无关,只与球壳的总电荷有关)
Shell Theorem #2 #
- 对于一个带电粒子,如果它位于一个带电球壳的内部,且球壳的电荷均匀分布在表面上,那么该粒子不会受到来自球壳的净电场作用力。 (即在球壳内部,电场为零)
Charge on Conducting Spherical Shell 导体球壳 #
- 一个中空的球形壳体,由导电材料制成
- 在一个导体球壳上,Charges会均匀地分布在其外表面,而不是内表面,这是因为导体内电荷会相互排斥,最终达到平衡分布
Conductor & Insulator 导体和绝缘体 #
- 我们通常可以根据Charge穿过它们的能力对材料进行分类
Conducting Path 传导路径 #
- 用羊毛摩擦铜棒时,电荷会从羊毛转移到铜棒,使铜棒带电。
- 如果此时握着铜棒,并接触一个与金属管道相连的水龙头,那么铜棒cannot be charged,这是因为人、铜棒、水龙头与地球表面通过管道形成了一条导电路径。多余的电荷会通过这条路径流向地球(地球是一个巨大的导体)。因此,铜棒上的电荷会扩散到地球表面,最终使铜棒变得电中性。
Grounding 接地 #
- 通过设置一条导体路径连接物体和地球,可以消除物体上的多余电荷,这个过程称为Grounding
Discharge 放电 #
- 这一个Grounding的将Exceed的Charge Neutralize的过程被称为Discharge
Charged Particles 带电粒子 #
- 原子由带正电的质子、带负电的电子和电中性中子组成
- 质子和中子紧密地堆积在一个原子核中
- 单个电子的电荷和单个质子的电荷具有相同的大小,但符号相反
Conduction electrons 价电子 #
- 在导体中Conduction electrons(价电子)因其与原子核的吸引力较弱而变得自由移动。
- 当导体原子形成固体结构时,这些导电电子在导体中形成“电子海”,可以在整个导体内自由流动
- 而在在绝缘体中,原子的电子与原子核结合得非常紧密,几乎没有自由电子
Induced Charge 感应电荷 #
- Induced Charge指的是由于邻近电荷的影响,导体内的电荷重新分布,形成正负电荷分离的现象
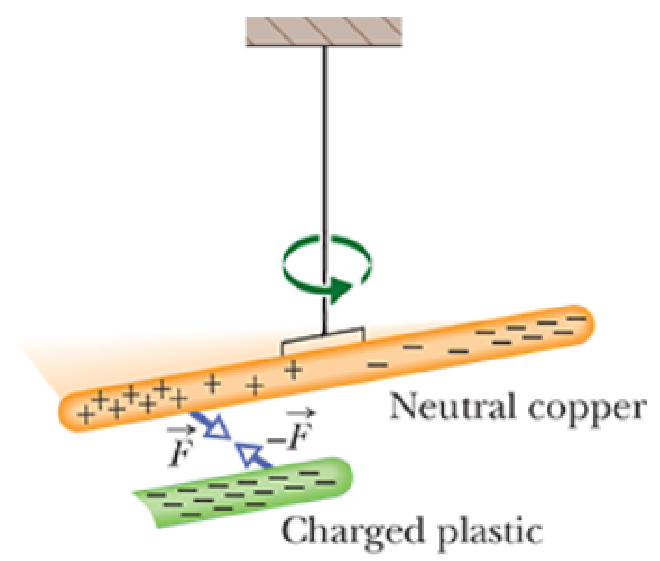
- 如图将一个Charged Plastic Rod放置到Neutral的Copper Rod旁边,Positive Charge将会被吸引到Copper Rod的左侧,Negative Charge则会被排斥到右侧,此时虽然Copper Rod是Neutral的,但其有一个 Induced Charge 感应电荷
- 需要注意的是,在Induced Charge形成的过程中,并不是Positive Charge移动了,而是因为原来均匀分布在整个Copper Rod上的Positive & Negative Charge中的Negative Charge移动了,所以才会有Positive Charge的出现
- 换句话说,Positive Charge不是“增加”来的,而是因为失去了Negative Charge,所以显得“正”
Charge is Quantized 量化电荷 #
- 在Benjamin Franklin的时代,电荷被认为是一种连续的流体——这个想法有很多用途。然而,我们现在知道流体本身,例如空气和水,不是连续的,而是由原子和分子组成的;物质是离散的
- 实验表明,Electrical fluid也不是连续的,而是由某种基本电荷的倍数组成。任何可以检测到的正电荷或负电荷 q 都可以写成
$$ q = n e, \quad n = \pm 1, \pm 2, \pm 3, \ldots $$
Charge of three Particles #
| Particle | Symbol | Charge | Antiparticle | Symbol | Charge |
|---|---|---|---|---|---|
| Electron | e or e⁻ | -e | Positron | e⁺ | +e |
| Proton | p | +e | Antiproton | p̅ | -e |
| Neutron | n | 0 | Antineutron | n̅ | 0 |
Electron的Symbol为e是因为其通常表示电子作为一种粒子的名称,而不特别强调它的电荷性质
Charge on two quarks #
| Quark | Symbol | Charge | Antiparticle | Symbol | Charge |
|---|---|---|---|---|---|
| Up | u | \(+\frac{2}{3}e\) | Antiup | \(\bar{u}\) | \(-\frac{2}{3}e\) |
| Down | d | \(-\frac{1}{3}e\) | Antidown | \(\bar{d}\) | \(+\frac{1}{3}e\) |
- 由于Quark不能单独存在(被限制在强相互作用中),我们通常不将它们的电荷视为基本电荷
Charge is Conserved 电荷守恒 #
- 摩擦不会产生电荷,而只会将其从一个物体转移到另一个物体,从而在此过程中破坏每个物体的电中性
- 任何孤立系统的净电荷总是守恒的,无论系统内部发生什么变化(如粒子的生成、湮灭或分裂),系统的总电荷量不会改变,下面给出一些常见的例子说明这一现象
Electron Capture 电子捕获 #
- 母核中的质子“捕获”原子的一个内部电子以形成中子(保留在子核中)并释放中微子
$$ p + e^- \rightarrow n + \nu $$