Last Edit: 3/24/25
Why N-T #
- 当已知了物体运动的轨迹的时候,可以更加简便的通过 Normal 法线,和 Tangential 切线坐标来描述粒子的运动
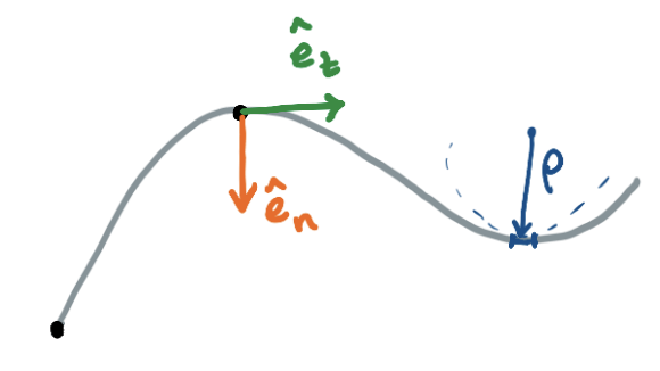
- t -axis:切线方向,与粒子所在位置的曲线切线方向一致,并且方向为粒子运动的正方向
- n -axis:法线方向,垂直于 t 轴,正方向指向曲线的曲率中心
- eₙ 和 eₜ:分别是法线和切线方向的单位向量
Radius of curvature 曲率半径 #
- Radius of Curvature 曲率半径是描述曲线在某点处弯曲程度的量度,具体来说,它是通过该点的曲线能够最佳拟合的圆的半径来定义的
$$ \rho = \frac{(1 + y’^2)^{3/2}}{|y’’|} $$
Distance in n-t System #
- 在一个 Circular Motion 中,物体移动的距离由 Radius of curvature 和滑过角度的积分得出,因为 Radius of Curvature 描述的就是在一点的曲线的完整圆的半径,半径乘以距离就得到了 Arc Length,具体来说有
$$ ds=\rho d \beta $$
Velocity in n-t System #
- 在 n-t 系统中,Velocity 的方向永远指向 Path of motion 的 tangent 方向,也就是说 V 就是 Tangent 方向上 V 的 Magnitude
$$ \vec{v} = v \vec{e}_t $$
- 同理在上面描述了 n-t System 中的 Distance,Velocity 也可以通过对其求导得到,有
$$ v = \dot{s} = \frac{ds}{dt} = \frac{\rho d\beta}{dt} = \rho \dot{\beta} \Rightarrow \vec{v} = v \vec{e}_t = \rho \dot{\beta} \vec{e}_t $$
- 这一个公式同时又可以推导出 Angle 关于 time 的导数,有
$$ \frac{d\theta}{dt} = \dot{\theta} = \frac{v}{\rho} $$
Acceleration in n-t System #
- 再次对 Velocity 求导就可以得到
$$ \vec{a} = \frac{d\vec{v}}{dt} = \frac{d \left( v \hat{e}_t \right)}{dt} = \dot{v} \hat{e}_t + v \frac{d\hat{e}_t}{dt} $$
- 其中,因为 Velocity 方向的导数由 Angle 的变化量决定,因为其本身 Magnitude 并不会发生改变,一直都是一,并且方向是圆心方向,所以有 \(d\hat{e}_t = d\theta \hat{e}_n\),带入得到
$$ \vec{a} = \dot{v} \hat{e}_t + v \frac{d\theta}{dt} \hat{e}_n = \dot{v} \hat{e}_t + \frac{v^2}{\rho} \hat{e}_n $$
- 而 a 的 Magnitude 就可以通过勾股定律得到
Tangential Acceleration #
- 总结上面的所有公式,可以得到
$$ a_t = \frac{dV}{dt} $$
Normal Acceleration #
- 同理对于 Normal 方向上的,有
$$ a_n = V \dot{\theta}=\rho \dot{\theta}^2 = \frac{V^2}{\rho} $$