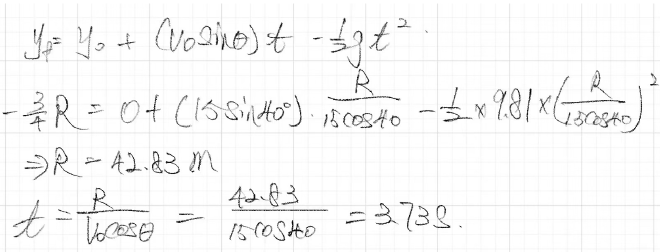Last Edit: 3/24/25
Assumptions #
- 斜抛运动其实就是在分析物体在两个自由度上的运动
- 现在为了简化问题,做出以下假设,忽略空气阻力,地球自转,并令重力为常数
Velocity #
- 于是有以下两个方向的初速度为
| Axis | Initial Velocity | Acceleration |
|---|---|---|
| x | \(v_0 \cos \theta\) | 0 |
| y | \(v_0 \sin \theta\) | \(\downarrow g, , -g \uparrow\) |
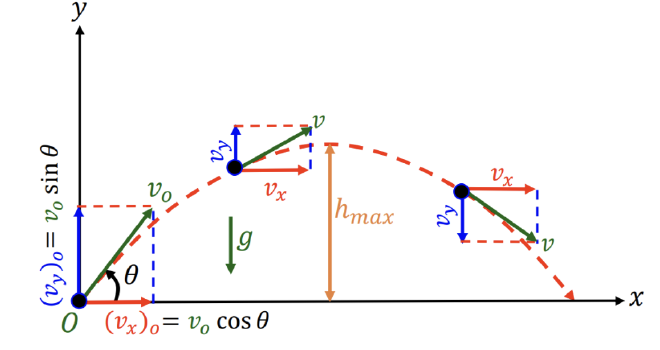
- 总结便可以得出以下表格
| Axis | Velocity (\(v = v_0 + at\)) | Position (\(s = s_0 + v_0t + \frac{1}{2}at^2\)) | No “t” (\(v^2 = v_0^2 + 2a\Delta s)\) |
|---|---|---|---|
| x | \(v_x = v_0 \cos \theta\) | \(x = x_0 + (v_0 \cos \theta)t\) | N/A |
| y | \(v_y = v_0 \sin \theta - gt\) | \(y = y_0 + (v_0 \sin \theta)t - \frac{1}{2}gt^2\) | \(v_y^2 = (v_0 \sin \theta)^2 - 2g\Delta y\) |
- 可以发现之所以x的第三列为 N/A 是因为 x 方向的加速度为零
Maximum Height #
- 通过分析这里的公式就可以得出一些二级结论
- 物体在 Projectile Motion 中到达最高点后的Velocity会降到0
- 到达这一点的时间可以通过 \(0=v_y-gt\) 得到,有
$$ t=\frac{v_y}{g} $$
- 其高度则是根据 \(v^2 = v_0^2 + 2a\Delta s\) 解得
$$ \Delta y = \frac{v_{y0}^2}{2g} $$
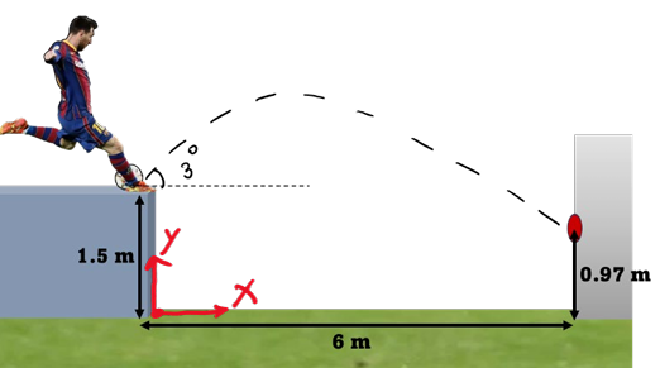
ex. Messi kicks the ball #
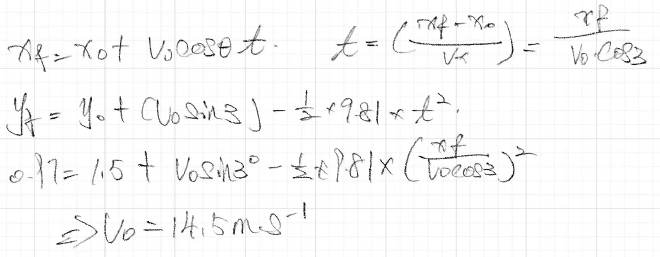
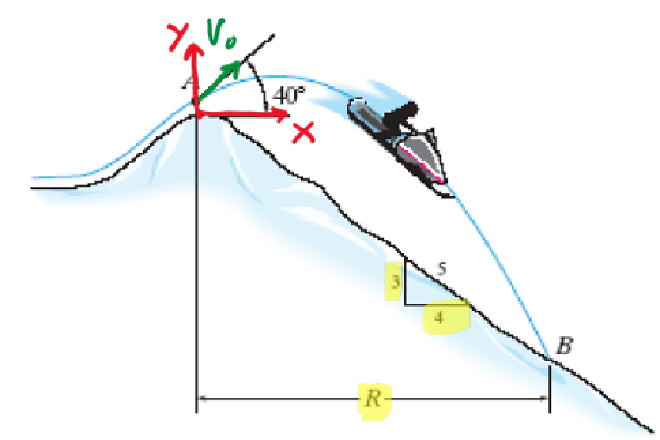
ex. Snowmobile #
Snowmobile is going 15 𝑚/𝑠 at point A. Find: The horizontal distance it travels (𝑅) and the time (𝑡) in the air