Last Edit: 3/24/25
Plane Curvilinear Motion #
- Plane Curvilinear Motion 是指物体在二维平面内沿曲线路径的运动。这种运动比直线运动复杂,因为物体的速度向量不仅大小可能变化,方向也在不断变
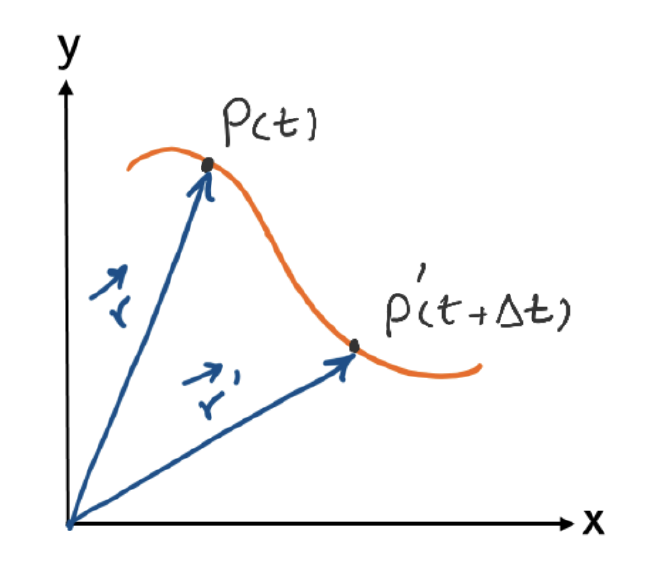
- 物体的运动轨迹是一条二维曲线,表示物体在x-y平面中的运动。
- 位置矢量 \(\vec{r}(t)\) 的是物体在时间t的时候从原点到物体当前所在位置的 Vector
- 轨迹点 P(t) 和 \(P’(t + \Delta t)\) 是物体在时刻t的位置
- 当时间t改变时,物体沿着曲线移动,位置矢量 \(\vec{r}\) 也会随时间变化
- 曲线运动中的速度和加速度是通过 \(\vec{r}(t)\) 的导数来确定的
$$ \vec{r}(t) = x(t)\hat{i} + y(t)\hat{j} $$
$$ \vec{v}(t) = \frac{d\vec{r}(t)}{dt} = \frac{dx(t)}{dt}\hat{i} + \frac{dy(t)}{dt}\hat{j} $$
$$ \vec{a}(t) = \frac{d\vec{v}(t)}{dt} = \frac{d^2x(t)}{dt^2}\hat{i} + \frac{d^2y(t)}{dt^2}\hat{j} $$
- 如果Velocity的Magnitude没有发生改变,其加速度依然存在,具体来说速度不仅与速度的大小变化相关,还与速度的方向变化相关
Instantaneous Direction 瞬时方向 #
- 对于曲线运动中的物体,当 \(\Delta t\rightarrow 0\) 的时候,其Displacement Vector和Velocity Vector总是与物体运动轨迹的 Tangent 方向一致
ex. Collision Problem in Plane #
The motions of two particles (A and B) are described by the position vectors. Find the point at which the particles collide and their speeds just before the collision
$$ \vec{r}_A = \left[ 3t , \hat{i} + 9t(2 - t) , \hat{j} \right] , \text{m} ,\vec{r}_B = \left[ 3(t^2 - 2t + 2) , \hat{i} + 3(t - 2) , \hat{j} \right] , \text{m} $$
- 想要做到碰撞,令i和j分别相等就行,之后就是求解了
Rectangular Coordinate System #
- 对于3D的情况,就是多了一个Freedom of motion其Position Vector以及Magnitude为
$$ \vec{r} = x\hat{i} + y\hat{j} + z\hat{k},|\vec{r}| = \sqrt{x^2 + y^2 + z^2} $$

Velocity #
- 同理只要对Position对时间t求导就是速度了
$$ \vec{v} = \frac{d\vec{r}}{dt} = \frac{d}{dt} \left( x\hat{i} + y\hat{j} + z\hat{k} \right) $$
$$ \vec{v} = \left( \frac{dx}{dt}\hat{i} + x\frac{d\hat{i}}{dt} \right) + \left( \frac{dy}{dt}\hat{j} + y\frac{d\hat{j}}{dt} \right) + \left( \frac{dz}{dt}\hat{k} + z\frac{d\hat{k}}{dt} \right) $$
- 由于i,j,k是Unit Vector,其不受时间影响,所以可以去掉
$$ vec{v} = \frac{dx}{dt}\hat{i} + \frac{dy}{dt}\hat{j} + \frac{dz}{dt}\hat{k} $$
Acceleration #
- 同理对速度求导就有
$$ \vec{a} = \frac{dv_x}{dt} \hat{i}+ \frac{dv_y}{dt} \hat{j} + \frac{dv_z}{dt} \hat{k} $$