D2L 3.1 Linear Regression
Last Edit 4/15/24
Regression 回归,是能为一个或多个自变量与因变量之间关系建模的一种方式
- [[Regression 回归]]
3.1.1 线性回归的基本元素 #
- Linear Regression 线性回归可以追溯到19世纪,其基于几个基本的假设
- 假设自变量与因变量之间为线性关系
- 假设噪声正常,如遵循正态分布
3.1.1.1 线性模型 #
- [[线性模型]]
- 线性假设是指目标可以表示为特征的加权和,如下例子
E.X. $$Price=w_{area}\cdot area+w_{age}\cdot age+b$$
- w称为Weight权重
- b称为Bias,Offset或者Intercept偏置,即特征为0时的预测值
严格来说,上式为输入特征的一个[[Affine Transformation 仿射变换]]
- 给定一个数据集,我们的目标即为寻找模型的Weight和Offset
高维数据集 #
- 在Deep Learning 领域,我们通常使用的是高纬数据集,建模时采用[[2.3 线性代数]]的表示方法会比较方便。
- 当我们的输入包含多个特征时,我们将预测结果表示为\(\hat{y}\)
点积形式 #
- 可以用点积形式来简洁的表达模型\(x\in R^d,w\in R^d\) $$\hat{y}=w^Tx+b$$
Model Parameters 模型参数 #
- 在开始寻找最好的模型参数前,我们还需要两个东西
一种模型质量的度量方式 #
一种能更新模型以提高预测质量的方式 #
3.1.1.2 损失函数 #
- 在开始考虑如何用模型Fit 拟合数据之前,我们需要一个拟合程度的度量
Loss Function 损失函数 #
- 量话目标的实际值和预测值之间的差距
- 通常选用非负数作为Cost,并且数值越小损失越小
平方误差函数 #
- 回归问题中最常用的Cost Function是平方误差函数 $$l^{(i)}(w,b)=\frac{1}{2}(\hat{y}^{(i)}-y^{(i)})^2$$
- 常数\(\frac{1}{2}\)的存在不会带来本质的差别,但当我们对这一方程求导后由于\(\frac{1}{2}\)的存在会使常数等于1
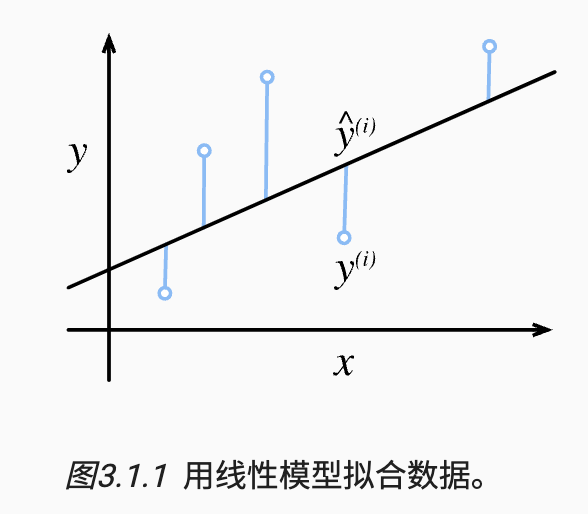
- 由于平方误差函数中的二次方项,会导致估计值和观测值之间较大的差异造成更大的损失。
- 为了度量模型在整个数据集上的质量,我们需要计算训练集上的样本损失均值 $$L(w,b)= \frac{1}{n}\Sigma^n_{i=1}l^{(i)}(w,b)=\frac{1}{n}\Sigma^n_{i=1}\frac{1}{2}(w^Tx^{(i)}+b-y^{(i)})^2$$
- 总的来说训练模型就是为了找到一组参数\(w^,b^\),其 $$w^,b^=argmin~L(w,b)$$
3.1.1.3 解析式 #
- 线性回归是一个很简单的优化问题,与大部分模型不同,其解可以用一个公式简单的表达出来,这类解便称为Analytical Solution 解析解
3.1.1.4 随机梯度下降 #
- 即使在无法得到解析解的情况下,我们可以有效的训练模型
Gradient Descent 梯度下降 #
- 最简单的方法就是计算Cost Function关于模型参数的导数(梯度)
- 但由于每次操作前都需要遍历整个数据集,导致执行速度非常之慢
- 所以通常会在每次更新时候抽取一小批样本,即为Minibatch Stochastic Gradient Descent 小批量随机梯度下降
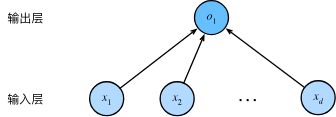
SGD #
- Minibatch Stochastic Gradient Descent 小批量随机梯度下降
- 每次迭代中,我们首先随机抽样一个小批量B, 它是由固定数量的训练样本组成的。 然后,我们计算小批量的平均损失关于模型参数的导数(也可以称为梯度)。 最后,我们将梯度乘以一个预先确定的正数,并从当前参数的值中减掉 $$(w,b)\leftarrow(w,b)-\frac{\eta}{|B|}\Sigma_{i\in B}\partial_{w,b}l^{(i)}(w,b)$$
- 初始化模型参数的值
- 从数据集中随机抽取小批量样本在负梯度方向上更新参数,并一直迭代
- \(\eta\)表示Learning Rate 学习率
- B表示Batch Size 批量大小
Hyperparameter 超参数 #
- 这些可以调整但不在训练过程中更新的参数称为超参数
- Hyperparameter Tuning为调整Hyperparameter的过程
- 而训练迭代结果是在独立的验证数据集(validation dataset)上评估得到的
收敛 #
- Linear Regression只会让预测值无限接近于实际值而却不能在有限的步数内非常精确地达到最小值
Generalization 泛化 #
- 寻找到一组合适的Hyperparameter纵然困难,但更加困难的是找到一组参数,这组参数能够在我们从未见过的数据上实现较低的损失, 这一挑战被称为Generalization 泛化
3.1.1.5 用模型进行预测 #
- 需要指出的是,Deep Learning对于实际值的接近更多是一种Prediction预测而非Inference推断
3.1.2 矢量化加速 #
- 为了同时处理整个小批量的样本,同时防止在python中编写开销高昂的for循环
矢量化性能测试 #
- 实例化两个全为1的10000维向量,采取两种处理方式,Python的for循环和对+的调用
###初始化两个Tensor
n = 10000
a = torch.ones([n])
b = torch.ones([n])
###用for循环完成一次
c = torch.zeros(n)
timer = Timer()
for i in range(n):
c[i] = a[i] + b[i]
f'{timer.stop():.5f} sec'
###用线性代数完成矢量化运算
timer.start()
d = a + b
f'{timer.stop():.5f} sec'
- 得到的结果为 0.167sec 和0.00042 sec
3.1.3 正态分布与平方损失 #
- 接下来,我们通过对噪声分布的假设来解读平方损失目标函数
正态分布 #
- [[Normal Distribution 正态分布]]
均方误差损失函数 #
- 均方损失可以用于线性回归的一个原因是:我们假设了观测中包含噪声,其中噪声服从正态分布,如下 $$y=w^Tx+b+\epsilon$$
- \(\epsilon\)代表了噪声
Likehood 似然 #
- [[Likehood 似然]]
- 通过给定的x观测到特定y的似然(likelihood) $$p(y|x)=\frac{1}{\sqrt{2\pi \sigma^2}}exp(-\frac{1}{2\sigma^2}(y-w^Tx-b)^2)$$
- 对于似然函数\(L(\theta|data)=P(data|\theta)= \Pi^N_{i=1}P(x_i|\theta)\)
- 已知x的正态分布密度函数,也就是x(\(\theta\)取每个值的概率)
- 要求得给定x(\(\theta\))(其不固定,但遵循正态分布)观测到特点y的似然,得到公式 \(L(x|y)=P(y|x)\)
- 已知\(p(y|x)=\frac{1}{\sqrt{2\pi \sigma^2}}exp(-\frac{1}{2\sigma^2}(y-w^Tx-b)^2)\)
- 由于\(P(y|x)=\Pi^N_{i=1}P(y^{(i)}|x^{(i)})\)(由x的参数条件下观测到y的可能性为独立的N个子事件的乘积)
- 根据[[Maximum Likehood Estimation 极大似然估计]],参数w和b的最优值是使整个数据集的[[Likehood 似然]]最大的值
- 但又因为乘积最大化问题十分复杂,并且由于历史遗留问题,优化常说的不是最大化,而是最小化
- 所以我们需要通过最小化对数似然\(-logP(y|x)\),由此可以得到的数学公式为 $$-logP(y|x)=\sum\limits^n_{i=1}\frac{1}{2}log(2\pi\sigma^2)+\frac{1}{2\sigma^2}(y^{(i)}-w^Tx^{(i)}-b)^2$$
- 推导如下
- \(-logP(y|x)=-log\sum\limits^n_{i=1}\frac{1}{\sqrt{2\pi \sigma^2}}exp(-\frac{1}{2\sigma^2}(y-w^Tx-b)^2)\)
\(=-log\sum\limits^n_{i=1}\frac{1}{\sqrt{2\pi \sigma^2}}e^{(-\frac{1}{2\sigma^2}(y-w^Tx-b)^2)}\) \(=-log(\sum\limits^n_{i=1}\frac{1}{\sqrt{2\pi \sigma^2}})+\frac{1}{2\sigma^2}(y-w^Tx-b)^2\) \(=-log\sum\limits^n_{i=1}(2\pi\sigma^2)^{-\frac{1}{2}}+\frac{1}{2\sigma^2}(y-w^Tx-b)^2\) = \(\sum\limits^n_{i=1}\frac{1}{2}log(2\pi\sigma^2)+\frac{1}{2\sigma^2}(y-w^Tx-b)^2\) - 现在我们只需要假设�是某个固定常数就可以忽略第一项\(\sum\limits^n_{i=1}\frac{1}{2}log(2\pi\sigma^2)\),因为第一项不依赖于w和b
- 对于第二项,除了常数\(\frac{1}{\sigma^2}\)外,其余部分与[[#平方误差函数]]是一样的
平方误差函数 #
$$l^{(i)}(w,b)=\frac{1}{2}(\hat{y}^{(i)}-y^{(i)})^2$$
- 幸运的是,上面式子的解并不依赖于\(\sigma\)
- 因此,在高斯噪声的假设下,最小化均方误差等价于对线性模型的极大似然估计
3.1.4 从线性回归到深度网络 #
- 到目前,我只谈论了线性模型,而神经网络涵盖了更为丰富的模型,并且我们也可以用描述神经网络的方式来描述线性模型,从而把线性模型看作一个神经网络。可以用“层”符号来重写这个模型
3.1.4.1 神经网络图 #
-
制图表可以可视化模型中正在发生的事情,但该图只显示了链接模式,而不包含权重和偏置的值
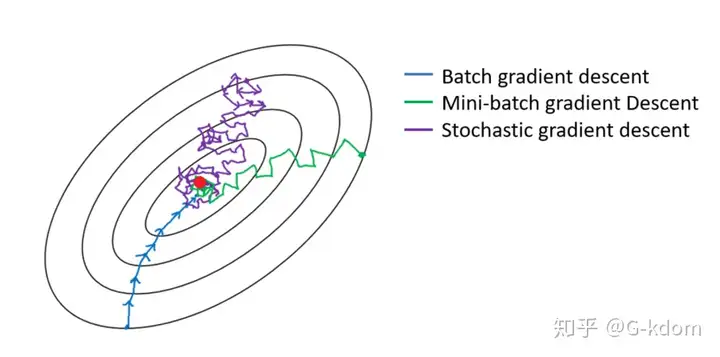
-
在上图中,输入为\(x_1,\dots x_d\),可知输入层的Feature Dimensionality 输入数(或称为特征维度)为d
-
网络的输出层为\(o_1\),因此输出层的输出数为1
-
需要注意的是,输入值都是已经给定的,并且只有一个_计算_神经元。 由于模型重点在发生计算的地方,所以通常我们在计算层数时不考虑输入层。
Fully-Connected Layer 全连接层 #
- 对于线性回归,每个输入都与每个输出(在本例中只有一个输出)相连, 我们将这种变换称为全连接层(Fully-connected layer)或称为稠密层(dense layer)。
3.1.4.2 生物学 #
-
即使观察真实的神经元,但当今大多数深度学习的研究几乎没有直接从神经科学中获得灵感
-
我们援引斯图尔特·罗素和彼得·诺维格在他们的经典人工智能教科书 Artificial Intelligence:A Modern Approach (Russell and Norvig, 2016) 中所说的:虽然飞机可能受到鸟类的启发,但几个世纪以来,鸟类学并不是航空创新的主要驱动力。 同样地,如今在深度学习中的灵感同样或更多地来自数学、统计学和计算机科学。