在了解多层感知机前,需要先了解[[Perceptron 感知机]]
4.1.1 隐藏层 #
- 在[[3.1_LinearRegression#3.1.1.1 线性模型]]中我们描述了[[Affine Transformation 仿射变换]],如一次函数一般是一种带有偏置项的线性变换
- 如果预测值在仿射变换后确实与输入数据有线性关系,那么这种方式确实够用
- 可是大部分情况下,仿射变换中的线性是一个很强的假设
4.1.1.1 线性模型可能会出错 #
- 线性意味着单调假设,权重w在正的情况下,任何特征的增大都会导致模型输出的增大
E.X.
- 如果我们试图预测一个人是否会偿还贷款,我们可以认为收入较高的申请人比收入较低的申请人更有可能偿还贷款
- 但上述例子只阐明了单调性而非线性
- 收入从0到5万会带来比100万到105万更大的还款可能性
- 在上例中,我们任然可以通过[[2.2 数据预处理]]的方式使线性更加合理,如对数化处理
- 但一个违反单调性的例子比如体温和死亡率的关系
- 对于体温高于37度的人来说,温度越高风险越高
- 而对于体温低于37度的人来说,温度越低风险就越低
- 这种情况也可以使用理37度的距离作为特征
- 分类问题,如对于猫狗分类问题,在位置(13,17)处像素强度进行添加,是否整个图像描绘狗的[[Likehood 似然]]会增加?
- 这一评估标准注定会失败,如倒置图像后,类别依然保留
- 对于上面两个例子来说,猫狗的分类问题无法通过简单的预处理解决
- 对于[[深度神经网络]],我们将使用隐藏层
4.1.1.2 在网络中加入隐藏层 #
-
我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制, 使其能处理更普遍的函数关系类型
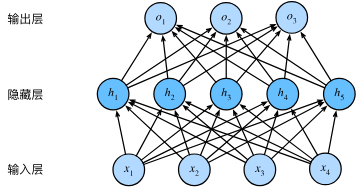
-
有全连接层的多层感知机的参数开销可能会高得令人望而却步。 即使在不改变输入或输出大小的情况下, 可能在参数节约和模型有效性之间进行权衡
4.1.1.3 从线性到非线性 #
-
同之前的章节一样,我们通过矩阵\(X\in R^{n\times d}\)来表示n个样本的小批量,其中每个样本具有d个输入特征
-
对于具有h个隐藏单元的单隐藏层多层感知机,用\(H\in R^{n\times h}\)表示隐藏层的输出,称为Hidden Representatiosn 隐藏表示
-
因为隐藏层和输出层都是全连接的, 所以我们有隐藏层权重\(W^{(1)}\in R^{R\times h}\)和隐藏层偏置\(b^{(1)}\in R^{1\times h}\)以及输出层\(W^{(2)}\in R^{h\times q}\)和输出层偏置\(b^{(2)}\in R^{1\times q}\)
-
所以形式上,对于单隐藏层的多层感知机的输出\(O\in R^{n\times q}\),有 $$\begin{align} \ H=WX^{(1)}+b^{(1)} \ O=HW^{(2)}+b^{(2)} \end{align}$$
-
现阶段,隐藏层为输入层的放射函数,而输出层为隐藏层的放射函数,即$$O=(XW^{(1)}+b^{(1)})W^{(2)}+b^{(2)}=XW+b$$
-
注意到现在在多层感知机的单隐藏层下,模型依然只做到了线性的放射函数
-
所以为了发挥多层架构的潜力,我们需要添加一个额外的关键要素:[[Activation Function 激活函数]],激活函数的输出则称为Activations 活性值
-
一般来说,有了激活函数,模型就不会退化成线性模型 $$\begin{align} \ H=\sigma(XW^{(1)}+b^{(1)}) \ O=HW^{(2)}+b^{(2)} \end{align}$$
-
为了构建更通用的多层感知机,我们可以继续堆叠这样的隐藏层,从而产生更有表达能力的模型
4.1.1.4 通用近似定理 #
- 多层感知机可以通过隐藏神经元,捕捉到输入之间复杂的相互作用, 这些神经元依赖于每个输入的值。 我们可以很容易地设计隐藏节点来执行任意计算
- 即使是网络只有一个隐藏层,给定足够的神经元和正确的权重, 我们可以对任意函数建模,尽管实际中学习该函数是很困难的
- 而且,虽然一个单隐层网络能学习任何函数, 但并不意味着我们应该尝试使用单隐藏层网络来解决所有问题。 事实上,通过使用更深(而不是更广)的网络,我们可以更容易地逼近许多函数。 我们将在后面的章节中进行更细致的讨论
4.1.2 激活函数 Activation Function #
- [[Activation Function 激活函数]]