QEC1.Rates&Returns
QEC1.Rates&Returns #
Last Edit: 9/8/25
1.1 Interest Rates & Return Measurement #
Interest Rates 利率 #
- Interest Rate measure the time value of money 衡量了货币的时间价值
Equilibrium Interest Rates 必要的回报率 #
- 对于某项投资,Equilibrium Interest Rates 反映了投资人期望的市场回报率
- 也代表了投资人为了出借资金所要求的 Return
Discount Rate 贴现率 #
- Discount Rate 可以被理解为衡量未来资金的现在价值的利率
- 因为有 Interest 的存在,未来的钱会增加,假设当前有 100 元,年利率为 5%,那么一年后 100 元会变成 105元
- 反过来说,如果希望一年后拿到 105 元,今天的价值则是 100 元,而这一比值就是 Discount Rate,把未来的钱转换成今天的价值的比率,有以下公式
$$ ⁍ $$
- PV(Present Value)= 现值,即今天的钱
- FV(Future Value)= 未来值,即未来的钱
- r(Discount Rate)= 贴现率
- t = 未来的时间(通常按年计算)
和 Interest Rate 的关系就是一个是顺着时间推移,一个是逆时间的反过程
Opportunity Cost 机会成本 #
- 例如一个一年期利率为 5%,投资者选择了消费而非储蓄,则 5% 就是放弃储蓄的 Opportunity Cost
Real Risk-Free Rate 无风险实际利率 #
- 定义:是单期贷款的 Theoretical Interest Rate,不考虑 Inflation 通货膨胀 或 Default risk 违约风险
- 经济学意义:衡量当前消费相对于未来消费的 Time Preference 时间偏好,也就是说同样的钱,不同时间下的价值就不同,Real Risk-Free Rate 就很好的衡量了不同时间下的价值
Time Preference 时间偏好 #
- 指的是人们对于“现在消费”和“未来消费”的偏好程度
- High Time Preference 更倾向现在消费放弃未来的收益
Real Rete of Return 实际收益率 #
- 定义:经过 Adjusting for inflation 通货膨胀调整后的投资者实际购买力收益
Nominal Risk-Free Rate 名义无风险利率 #
- 指的是没有 Default Risk 违约风险的金融工具,但其回报仍受 Inflation 通货膨胀影响
- 例如,美国国库券(T-bills)的利率属于 Nominal Risk-Free Rate,但包含 Inflation Premium 通胀溢价
- 也就是说 Nominal Risk-Free Rate 和 Real Risk-Free Rate 和 Expected Inflation Rate 有关
$$ (1 + \text{Nominal Risk-Free Rate}) = (1 + \text{Real Risk-Free Rate}) \times (1 + \text{Expected Inflation Rate}) $$
- 这一关系有时候可以被近似为
$$ \text{Nominal Risk-Free Rate} \approx \text{Real Risk-Free Rate} + \text{Expected Inflation Rate} $$
Inflation Premium 通胀溢价 #
- 是投资者要求的额外回报,用于补偿未来 Inflation 可能带来的货币购买力下降,这个额外的回报,就是 Inflation Premium,有
$$ \text{Inflation Premium} = \text{Nominal Risk-Free Rate} - \text{Real Risk-Free Rate}⁍ $$
ex. Inflation Premium at 3 inflation Rate #
- 存 100 元到银行,银行给 5% 的 Nominal Risk-Free Rate,但如果 Inflation Rate 是 3%,那么真正的购买力只增加了 2%(实际收益),这里的 Inflation Premium 就是 3 %
Risks 风险 #
- 对于一个投资,总结来说存在各种风险,其中的每一个风险都与一个 Risk Premium 所绑定,并会被夹到 Nominal Risk-Free Rates 上,于是 Nominal Risk-Free Rate 就变成了
$$ \text{nominal risk-free rate} \approx \text{real risk-free rate} + \text{expected inflation rate} $$
Default Risk 违约风险 #
- 当 Borrower 无法按时 make the promised payments 的风险
Liquidity Risk 流动性风险 #
- 当 Investment 无法 Sold Quick for cash 套现时所面临的风险
Maturity Risk 到期风险 #
- 债券的到期日越远,其价格对利率变动的敏感性越高,也就具有更高的 Maturity Risk
Holding Period Return HPR 持有期收益率 #
- HPR 计算出了投资在给定时间内价值的 Percentage Increase
$$ \text{holding period return} = \frac{\text{end-of-period value}}{\text{beginning-of-period value}} - 1 $$
- 单个持有期的HPR计算方法如下:
$$ \text{HPR} = \frac{P_t + \text{Div}}{P_0} - 1\frac{P_t - P_0 + \text{Div}}{P_0} $$
- \(P_t\) 表示持有期末的股票价格
- \(P_0\) 表示持有期初的股票价格
- \(\text{Div}\) 表示在持有期间支付的股息
Dividend 股息,指的公司盈利后把赚到的一部分分给 Shareholders 的形式
- 举例来说,如果一支股票在期初价格为20欧元,在持有期间支付了 1 欧元股息,期末价格为22欧元,那么HPR计算如下:
$$ \text{HPR} = \frac{22 + 1}{20} - 1 = 0.15 $$
- 这表明投资者在这个持有期间内的总回报率是15%
22 欧元是股票结束时候的市场价值
- 当考虑多个持有期的回报时,我们使用复合回报的概念,公式如下:
$$ \text{HPR} = (1 + \text{HPR}{\text{Year 1}})(1 + \text{HPR}{\text{Year 2}})(1 + \text{HPR}_{\text{Year 3}}) - 1 $$
- 这里,每个年度的HPR分别加1后相乘,然后再减1,这样可以计算出整个三年期间的总复合回报率
- 例如,如果第一年的回报率是5%,第二年是3%,第三年是7%,那么三年的总HPR计算如下:
$$ \text{HPR} = (1 + 0.05)(1 + 0.03)(1 + 0.07) - 1 \approx 0.1571 \text{ 或 } 15.71% $$
Annualized Return 年化回报率 #
- 最后,如果回报需要跨多年计算,通常会使用年化回报率而不是简单的HPR
- 年化回报率考虑了投资期间的具体长度,并将回报率调整为年度等效值,使得不同期间长度的投资回报率可以公平比较
Average Returns #
- 一般来说存在两种计算 Average Returns 的方式,Arithmetic 和 Geometric Mean,也就是算术和几何平均收益率
Arithmetic Mean Return 算数平均收益 #
- 最简单的计算 Average 的方式
$$ \text{arithmetic mean return} = \frac{R_1 + R_2 + R_3 + \dots + R_n}{n} $$
- 直接计算所有值的总和,然后除以总个数。
- 适用于独立数据的均值,例如考试成绩、股市单日涨跌平均值等。
Geometric Mean Return #
- 当每个 Period 的 Rate of return 不同的时候,Geometric Mean Return 可以用来计算 Compound Rate,当每个 Period 回报率波动比较大的时候,GM 通常小于 AM
$$ \text{geometric mean return} = \sqrt[n]{(1 + R_1) \times (1 + R_2) \times (1 + R_3) \times \dots \times (1 + R_n)} - 1 $$
- 先将所有值相乘,再开 n 次方(对数平均)
- 适用于复利增长或波动性较大的数据,例如投资回报、人口增长率等
| 类型 | 适用情况 | 示例 |
|---|---|---|
| 算术平均数(AM) | 适用于加法关系的数据,求一组数值的直接平均 | - 计算学生考试平均分- 计算不同年份的气温平均值 |
| 几何平均数(GM) | 适用于乘法关系的数据,求一组数的复合增长率 | - 计算股票的年均回报率- 计算 GDP 增长率 |
ex. Calculate Geometirc Mean #
Acme 公司普通股在过去三年的回报率分别是 -9.34%、23.45%、8.92%,求该股票的Compound annual rate of return
$$ R_G = \sqrt[3]{(1 - 0.0934) \times (1 + 0.2345) \times (1 + 0.0892)} - 1 $$
- 因此,该股票的几何平均回报率约为 6.825%
ex. Calculater GM in shorter period #
- 给出四个 Semiannual periods 的回报率分别为 2.0%、0.5%、-10.0%、1.5%
$$ \text{Geometric mean} = \sqrt[4]{(1 + 0.02)(1 + 0.005)(1 - 0.10)(1 + 0.015)} - 1 = 0.7435% $$
- 几何平均回报约为 0.7435%,这是6个月持有期的回报。
- 由于四个半年期等于两年,为了获得 Annual return ,我们需要取 2 作为开方的根数:
$$ \text{Annual return} = \sqrt[2]{(1 + 0.02)(1 + 0.005)(1 - 0.10)(1 + 0.015)} - 1 = 1.49\ % $$
- 最终,年化回报为 1.49%
Harmonic Mean 调和平均数 #
- Harmonic Mean 常常用在速率,比率这类场景中,例如计算股票购买的平均成本,有
$$ X_H = \frac{N}{\sum \frac{1}{X_i}} $$
- 其中 N 为数据个数,\(X_i\) 为各个数值
ex. Harmonic Mean #
- 一位投资者每月投资 1,000 购买股份。在过去三个月内,每股支付的价格分别为 8、\(9、\)10,求 Harmonic Mean
$$ X_H = \frac{3}{\frac{1}{8} + \frac{1}{9} + \frac{1}{10}} = 8.926 $$
- 平均成本价约为 $8.926 每股。
- 验证方法:计算总购买股份数
$$ \frac{1,000}{8} + \frac{1,000}{9} + \frac{1,000}{10} = 336.11 \text{ shares} \frac{3,000}{336.11} = 8.926 \text{ per share} $$
- 对于上面的三个 Mean Values,他们之间有一个数学关系,即
$$ \text{Arithmetic mean} \times \text{Harmonic mean} = (\text{Geometric mean})^2 $$
- 同时,HM<GM<AM
1.2 Time-Weighted And Money-Weighted Returns #
- 比较 Money-Weighted Rate of return 资金加权收益率,和 Time Weighted Rate of Return 时间加权收益率,来评估投资组合的表现
Money-weighted Rate of Return 资金加权收益率 #
- MWRR 和 IPR 实际上使用的是相同的计算公式,两者仅在语境上不同,IPR 多用在项目,公司投资商,MWRR 则是个人投资中用的多,但两者都计算了资金投入时间的加权效果
- IPR 即内部收益率,是一种衡量投资收益的方式
- 其核心思路是:找出一个年收益率,使得“所有现金流”的现值加起来刚好等于 0
投资的钱是流出,收到的钱是流入。把这些现金流按照某个收益率来“折现”之后,加起来为 0,那这个收益率就是 IRR
ex. #
- 举例来说,在 t = 0 时,投资者买入 1 股,花了 100 这是流出,\(C(0)=-100\)
- t = 1 时,再次买入 1 股,花了 120,同时在年末收到了 2 的 Dividend(股息),\(C(1)=-120+2=-118\)
- t = 2 时,卖出 2 股,收到 130,同时受到每股 2 的 Share Dividend(股息),\(C(3)=1302+22=264\)
| 年份(t) | 现金流(Cash Flow) |
|---|---|
| 0 | -100 |
| 1 | -120 |
| 2 | +134 |
- 到了这一步后,就可以开始求 IPR 了,回顾 IPR 含义,一个能使得“所有现金流”的现值(向前贴现)加起来刚好等于 0 的年收益率
- 也就是说要求一个 r,让下面这个等式成立:
$$ -100 + \frac{-118}{(1 + r)} + \frac{264}{(1 + r)^2} = 0 $$
- 把所有的现金流都 Discount(折现)回 t = 0 时刻,使总和为 0
- 这个 r,就是 money-weighted rate of return(货币加权收益率),也就是投资的 IRR
- 最后可以解出 \(r\approx13.86%\)
- 这个 r 的含义就是,整体的投资等同于把两笔钱在两个时间,2 年前和 1 年前的时候分别放入一个年收益率为 13.86 的账户中
Time-weighted Rate of Return #
- 衡量的是 投资组合本身的复利增长率,不受资金流入流出时机的影
- 在实际应用中,这个指标常用于评价 Fund Manager(资金经理)的投资能力,因为 Fund Manager 无法控制投资者何时申购或赎回
-
分段计算(每次有资金流入或流出时,把整个期间拆开)
-
算每一段的持有期收益率(HPR, Holding Period Return 持有期收益率)
$$ HPR = \frac{期末价值 + 分红}{期初价值} - 1 $$
-
几何平均:
$$ (1+TWRR)^n = \prod (1+HPR_i) $$
Ex. #
-
用和 MWRR 一样的例子
-
第一年 (t=0 → t=1)
- 初始:100 美元
- 年末:120 美元市值
- 股息:2 美元
- \(HPR₁ = (120 + 2) / 100 - 1 = 22%\)
-
第二年 (t=1 → t=2)
- 初始:240 美元(两股,每股120)
- 年末:260 美元市值
- 股息:4 美元
- \(HPR₂ = (260 + 4) / 240 - 1 = 10%\)
-
总收益率(Geometric Mean)
$$ (1+TWRR)^2 = (1.22)(1.10) $$
$$ TWRR = \sqrt{1.342} - 1 = 15.84% $$
MWRR V.S. TWRR #
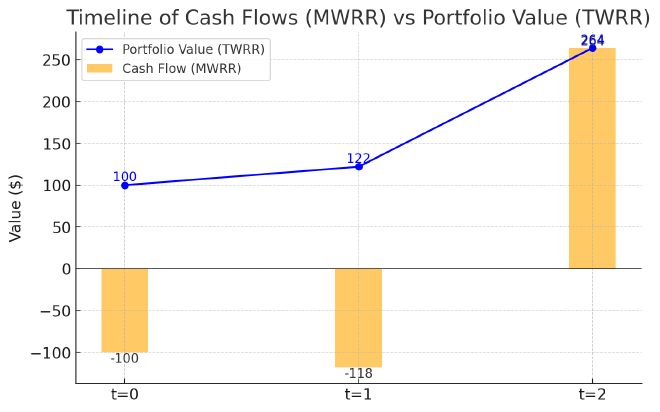
- Money-weighted return (MWRR) = 13.86%
- Time-weighted return (TWRR) = 15.84%
- 差异原因:
- MWRR 给了 更多权重 给 第二年,因为在第二年时资金更多(两股)
- 第二年收益率只有 10%,低于第一年的 22%,所以 MWRR < TWRR
- TWRR 完全去掉了资金流入流出的影响,只反映投资本身的复利效果
- MWRR(13.86%):体现的是投资者个人的真实收益体验,取决于资金投入的时机
- TWRR(15.84%):体现的是投资本身的表现,不受投入时机影响,更适合评价基金经理
1.3 Common Measures of Return #
- Return 收益率存在多种度量方式
Annualized Return(年化收益率) #
-
定义:把一个 HPR, Holding Period Return 持有期收益率换算成一年期的等效收益率
-
公式:
$$ \text{annualized return} = (1+HPR)^{365/days} - 1 $$
-
例子 1(不足一年):
存 100 美元,90 天后变 100.75 美元
- \(HPR = (100.75 − 100)/100 = 0.75%\)
- \(年化 = (1 + 0.0075)^{(365/90)} − 1 ≈ 3.08%\)
-
例子 2(超过一年):
买一张 500 天国债,970 → 1000。
- \(HPR = (1000 − 970)/970 = 3.09%\)
- \(年化 = (1 + 0.0309)^{(365/500)} − 1 ≈ 2.25%\)
👉 作用:不同持有期的收益率可以统一比较
Compounding Frequency(复利频率) #
-
名义年利率 r(quoted annual interest rate)不变,但复利次数 m 越多,有效利率越高
-
现值公式:
$$ PV = FV \cdot (1 + r/m)^{-mN} $$
PV:Present Value,FV:Future Value
例子:未来一年收到 1000 美元,贴现率 6%
- 年复利 (m=1): \(PV = 943.40\)
- 半年复利 (m=2): \(PV = 942.60\)
- 季度复利 (m=4): \(PV = 942.18\)
- 月复利 (m=12): \(PV = 941.91\)
- 日复利 (m=365): \(PV = 941.77\)
👉 复利次数越多,现值越低(贴现率并不变)
Continuously Compounded Return(连续复利收益率) #
-
定义:当复利频率趋近于无穷时,得到连续复利收益率。
-
公式:
$$ R_{cc} = \ln(1+HPR) = \ln\left(\frac{\text{ending value}}{\text{beginning value}}\right) $$
-
例子:100 → 120
- \(HPR = 20%\)
- \(连续复利收益率 = ln(1.2) = 18.232%\)
👉 好处:连续复利收益率是 可加的,多个区间的连续收益率可以直接相加,便于计算
Comparing #
| 指标 | 特点 | 公式 | 适用场景 |
|---|---|---|---|
| HPR(持有期收益率) | 不考虑时间长短 | \((期末价值 + 分红) / 期初价值 - 1\) | 单一投资期间 |
| Annualized Return(年化收益率) | 统一成一年期 | \((1+HPR)^{(365/days)} - 1\) | 跨不同持有期比较 |
| 有限复利 | 考虑 m 次复利 | \((1+r/m)^(mN)\) | 银行利率、债券 |
| 连续复利 (Rcc) | 极限情况,可加性 | \(ln(1+HPR)\) | 数学推导、衍生品定价 |
以上三个 Returns 主要看时间维度的收益率变化,接下来要研究的是可能造成收益率变化的因素
Gross return vs Net return #
-
Gross return(毛收益率)
投资组合的总回报,在扣除交易佣金和费用之前
-
Net return(净收益率)
扣除了佣金、管理费等必要费用后的回报
👉 更能反映投资者最终拿到的收益。
Pretax nominal return vs After-tax nominal return #
-
Pretax nominal return(税前名义收益率)
投资在交税之前的收益,比如股息、利息、资本利得
-
After-tax nominal return(税后名义收益率)
扣除了税收之后的收益,才是真正到手的部分
Real return(实际收益率) #
- 定义:名义收益率剔除通货膨胀(inflation)后的收益率,代表 购买力的实际增长
公式:
$$ 1+ \text{real return} = \frac{1+\text{nominal return}}{1+\text{inflation rate}} $$
例子:
- \(名义收益率 = 7%\)
- \(通胀率 = 2%\)
- \(实际收益率 = (1.07 / 1.02) − 1 = 4.9%\)
👉 投资赚了 7%,但通胀吞掉了 2%,所以实际购买力只提高了约 5%
Leveraged return(杠杆收益率) #
- 定义:当投资者使用借贷(leverage)来放大投资时,得到的收益率
公式:
$$ \text{leveraged return} = \frac{r \times (V_0 + V_B) - r_B \times V_B}{V_0} $$
其中:
- \(V_0\):自有资金
- \(V_B\):借入资金
- \(r\):投资收益率
- \(r_B\):借款利率
👉 杠杆放大了风险和收益:涨的时候收益率更高,跌的时候亏损更惨
Comparing #
| 指标 | 关注点 | 是否考虑通胀 | 是否考虑税收 | 是否考虑杠杆 |
|---|---|---|---|---|
| Gross return | 毛收益率,不含费用 | 否 | 否 | 否 |
| Net return | 扣费后的收益率 | 否 | 否 | 否 |
| Pretax nominal return | 税前名义收益率 | 否 | 否 | 否 |
| After-tax nominal return | 税后名义收益率 | 否 | 是 | 否 |
| Real return | 实际收益率(剔除通胀) | 是 | 可加上 | 否 |
| Leveraged return | 杠杆收益率 | 可包含 | 可包含 | 是 |
✅ 一句话总结:
- 毛/净收益率 → 是否扣费用
- 税前/税后收益率 → 是否扣税
- 名义/实际收益率 → 是否剔除通胀
- 杠杆收益率 → 是否使用杠杆