Last Edit: 1/22/25
Sequences #
- Sequence是按照一定顺序排列的一列数。序列可以是有限的也可以是无限的,通常表示为\(a_1, a_2, a_3, \ldots\),其中\(a_n\)表示序列的第n项
Limit of a Sequence #
- 对于一个Sequence,如果有 $$\lim_{n\rightarrow\infty}a_n=L,L\in \mathbb R$$
- 则该Sequence的Limit为L
- 如果存在这个L,也可以说Sequence是Converge 收敛的
- 如果不存在,则Sequence Diverge 发散
ex. Nature Number #
- 找到Sequence \(a_n = \left(1 + \frac{1}{n}\right)^n\)的Limit $$\lim_{n \to \infty} a_n = \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n = e$$
Properties of Limits of Sequences #
- Let \(\lim_{n \to \infty} a_n = L \text{ and } \lim_{n \to \infty} b_n = K\) $$\lim_{n \to \infty} (a_n \pm b_n) = L \pm K$$ $$\lim_{n \to \infty} c a_n = cL$$ $$\lim_{n \to \infty} (a_n b_n) = LK$$ $$\lim_{n \to \infty} \frac{a_n}{b_n} = \frac{L}{K}$$
Squeeze Theorem for Sequences #
- Squeeze Theorem也可以用来解Sequence的Convergence,其通常用在 \((-1)^n, \sin(x)\)等在\(n\rightarrow \infty\)时oscillate的函数中
ex. Sequence Convergence by Squeeze Theorem #
- 证明Sequence \({ c_n } = \left{ (-1)^n \frac{1}{n!} \right}\)收敛
- 使用两个序列\(a_n=\frac{1}{2^n}\),已知Factorial的扩散速度小于Exponential,有 $$-\frac{1}{2^n} \leq (-1)^n \frac{1}{n!} \leq \frac{1}{2^n}, \quad n \geq 4$$
Monotonic Sequences #
- 当一个Sequence的每一项都单调递增或单调递减时,该Sequence被称为Monotonic Sequence
Bounded Sequence #
Bounded Above #
- 当存在一个\(M\in \mathbb R\)使得\(a_n\leq M\)时,称该Sequence Bounded Above
Bounded Below #
- 当存在一个\(M\in \mathbb R\)使得\(a_n\geq M\)时,称该Sequence Bounded Below
Bounded #
- 当一个Sequence同时Bounded Above和Below的时候,其Bounded
Theorem - Convergent Sequence are Bounded #
- 如果一个Sequence Convergent,则其一定Bounded
- 同理也可以反推,如果一个Sequence Bounded并且是Monotonic 单调的Sequence的话,该Sequence Convergent 收敛
Series (Infinite Series) #
- 对于Sequence来说,它的所有项相加的和便成为了Series $$S_n=\sum_{n=1}^{\infty} a_n = a_1 + a_2 + a_3 + \cdots + a_n + \cdots$$
Convergent of Series #
- 对于一个Series \(\sum^\infty_{n=1}a_n\)来说,如果其Partial Sum(前n项之和)等于S,则该Series Converge,反则Diverge
Telescoping Series 列项级数 #
- 通过将级数的两个项组合得到一个新的通项公式求得级数的解
ex. Finding Series Convergency by Telescoping #
- 求解\(\sum_{n=1}^{\infty} \frac{2}{4n^2 - 1}\) $$a_n = \frac{2}{4n^2 - 1} = \frac{2}{(2n - 1)(2n + 1)} = \frac{1}{2n - 1} - \frac{1}{2n + 1}$$
- 通过观察规律可以看出 $$S_n = \left( \frac{1}{1} - \frac{1}{3} \right) + \left( \frac{1}{3} - \frac{1}{5} \right) + \cdots + \left( \frac{1}{2n-1} - \frac{1}{2n+1} \right) = 1 - \frac{1}{2n+1}$$
- 最终得出 $$\sum_{n=1}^{\infty} \frac{2}{4n^2 - 1} = \lim_{n \to \infty} S_n = \lim_{n \to \infty} \left(1 - \frac{1}{2n+1}\right) = 1$$
Geometric Series #
- 形如\(\sum_{n=0}^{\infty} ar^n\)的Series被称为Geometric Series,其完整形式为 $$\sum_{n=0}^{\infty} ar^n = a + ar + ar^2 + \cdots + ar^n + \cdots, \quad a \neq 0$$
Convergenvce of Geometric Series #
- 当Geometric Series的的敛散性高度取决于其公比r的取值
- 具体来说当\(0<|r|<1\) Geometric Series Converge ,当\(|r|\geq 1\),其Diverge
The Value Geometric Series Converge to #
- Geometric Sereis是很特别的一个Series,于大部分Series不同,当其Converge的时候可以简单的求出Series的值为 $$\lim_{n \to \infty} S_n = \lim_{n \to \infty} \left[ \frac{a(1 - r^n)}{1 - r} \right] = \frac{a}{1 - r} \lim_{n \to \infty} (1 - r^n) = \frac{a}{1 - r}$$
Property of Infinite Series #
- 如果\(\sum a_n\)和\(\sum b_n\)都是Converge的Series,并且分别收敛到A和B,则有 $$\sum_{n=1}^{\infty} c a_n = cA$$ $$\sum_{n=1}^{\infty} (a_n + b_n) = A + B$$ $$\sum_{n=1}^{\infty} (a_n - b_n) = A - B$$
p-Series and Harmonic Series #
$$\sum_{n=1}^{\infty} \frac{1}{n^p} = \frac{1}{1^p} + \frac{1}{2^p} + \frac{1}{3^p} + \cdots$$
Convergence of p-Series #
- 当 \(p>1\) 的时候Converge,\(0<p\leq 1\) 的时候Diverge
Harmonic Series #
- 当p=1时,p-Series变成其特殊形式,即Harmonic Series
Alternating Series #
- 到目前为止的Series都只含有Postitive的Terms
- Alternating Series 交错级数指的是一正一负(一负一正)的Terms的级数
Alternating Series Remainder #
- 如果一个收敛的交错级数满足以下条件:
- \(a_{n+1} \leq a_n\)(即正项部分单调递减),\(\lim_{n \to \infty} a_n = 0\),
- 那么,当用第N项部分和\(S_N\)来近似整个级数的和 SS 时,有 $$|S - S_N| = |R_N| \leq a_{N+1}$$ 换句话说,误差的绝对值小于等于被忽略的第一个正项\(a_{N+1}\)
Absolute and Conditional Convergence #
- 有的Series可能含有正负项,但他们不已一定规律出现
- 这时候就需要利用Absolute and Conditional Convergence
- 如果一个级数 \(\sum |a_n|\) Convergence Absolutly(即级数的项的绝对值构成的级数收敛),则原级数 \(\sum a_n\) 也一定Converge
Conditionally Converge #
- 对于一个Series,当\(\sum |a_n|\) Diverge但是\(\sum a_n\) converge的时候,其Conditionally Converge 条件收敛
Tests for Convergency #
- 对于Series存在许多的判断其是否收敛的办法
The Integral Test #
- 如果函数f(x)满足以下条件:f(x)在 \(x \geq 1\) 上是positive,continuous,decreasing的,则: $$\sum_{n=1}^\infty a_n与\int_{1}^\infty f(x), dx$$
- 的收敛性是一致的: 要么两者都收敛,要么两者都发散
Direct Comparison Test #
- 假设存在两个正项级数 \(\sum a_n\) 和 \(\sum b_n\),并且对所有n都满足 \(0 < a_n \leq b_n\),则有:
- 如果 \(n\sum b_n\) Converge,则 \(\sum a_n\) 也Converge
- 如果 \(\sum a_n\) Diverge,则 \(\sum b_n\) 也Diverge
Limit Comparison Test #
- 对于Direct Comparison能做的,Limit都能做到并且会更加简单 假设存在两个正项级数 \(\sum a_n\) 和 \(\sum b_n\),并且满足:
\(a_n > 0\) 和 \(b_n > 0\) 对所有n成立,存在极限: \(\lim_{n \to \infty} \frac{a_n}{b_n} = L\) 其中\(0 < L < \infty\)
- 如果 \(\sum b_n\) Converge,则 \(\sum a_n\) 也Converge
- 如果 \(\sum b_n\) Diverge,则 \(\sum a_n\) 也Diverge
Throrem - nth Test #
- If \(\lim_{n \to \infty} a_n \neq 0\), then \(\sum_{n=1}^{\infty} a_n\) diverges
Alternating Series Test #
- 对于形式为交错级数的两个级数: $$\sum_{n=1}^\infty (-1)^n a_n \quad \text{和} \quad \sum_{n=1}^\infty (-1)^{n+1} a_n$$
- 如果满足以下两个条件,则级数收敛:
- \(\lim_{n \to \infty} a_n = 0\),\(a_{n+1} \leq a_n\) 对所有n成立(即\({a_n}\)是单调递减的正项数列)。
Ratio Test #
- Let \(\sum a_n\) be a series with nonzero terms
- 当\(\lim_{n \to \infty} \left| \frac{a_{n+1}}{a_n} \right| < 1\),级数Converges Absolutely
- 当\(\lim_{n \to \infty} \left| \frac{a_{n+1}}{a_n} \right| > 1 \text{ or } \lim_{n \to \infty} \left| \frac{a_{n+1}}{a_n} \right| = \infty\),级数Diverge
- 当\(\lim_{n \to \infty} \left| \frac{a_{n+1}}{a_n} \right| =1\)时,Ratio Test失效
简单解释一下原理就是通过转化为Geometric Series后计算公比
The Root Test #
- Let \(\sum a_n\) be a series with nonzero terms
- 当\(\lim_{n \to \infty} \sqrt[n]{|a_n|} < 1\)时,级数Converge Absolutely
- 当\(\lim_{n \to \infty} \sqrt[n]{|a_n|} > 1 \text{ or } \lim_{n \to \infty} \sqrt[n]{|a_n|} = \infty\)时,Diverge
- 同理\(\lim_{n \to \infty} \sqrt[n]{|a_n|} = 1\)时失效
Taylor Polynomials and Approximations #
- 想要通过一个Polynomial来近似一个function,首先找到一点c,其在function的domain中,再给与\(p(c)\)和\(f(c)\)相同的值,就可以说这个Polynomial是以c点为中心近似function的
- 由于过一个点的Polynomial非常之多,所以更一步的近似就是同时令function和polynomial在点c处的slope也相似,有\(p’(c)=f’(c)\)满足了以上两个条件,就获得了一个简单的对于function的近似
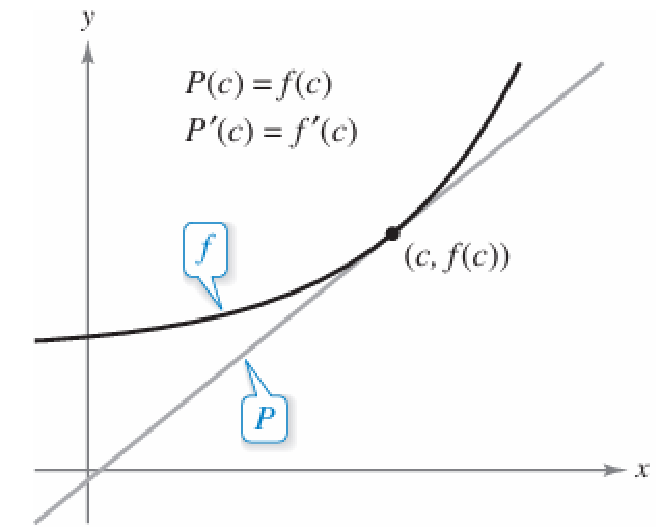
ex. First Degree Approximation for e^x #
- \(f(x)=e^x\) 存在一个特殊的性质,就是其derivate等于原函数,于是有 $$f(0)=f’(0)=e^0=1$$
- 现在拿出一个One degree polynomial \(p(x)=a_0+a_1x\),分别对齐\(p(0)\)和\(p’(0)\)
- \(p(0)=a_0+0=1\Rightarrow a_0=1\),\(p’(0)=a_1=1\Rightarrow = a_1 =1\)
- 可以得到\(p(x)=1+x\),就这样逐渐的往高阶逼近,Polynomial和Function以c为中心的逼近也会越来越精确
Taylor Polynomials #
- 在上面的例子中,多项式是以\(c=0\)为中心approximate function的,而这一个c可以根据需要进行调整,具体来说这个多项式在n阶下应该为 $$P_n(x) = a_0 + a_1(x-c) + a_2(x-c)^2 + a_3(x-c)^3 + \cdots + a_n(x-c)^n$$
- 这一个polynomial中存在三个参数,其中c为常数,x为variable,于是就要求解a的值
- 在前面的例子中提到了求解\(a_0,a_1\)的办法,具体就是令\(p_n^{(n)}(c)=f_n^{(n)}(c)\)
- 观察polynomial求到第n阶导数的样子,有 $$P_n’’’(x) = 2(3a_3) + \cdots + n(n - 1)a_n(x - c)^{n-3}$$ $$P_n^{(n)}(x) = n(n - 1)(n - 2) \cdots (2)(1) a_n$$
- 可以发现求解\(a_n\)的关键就在于当P求到第n阶导数的时候\((x-c)^n\)这一项会只剩下系数(z)乘以\(a_n\),也就是\(za_n(x-c)^0\)(具体系数等于多少稍后讨论),那么这时候令\(x=c\),所有高次的项均会被消去只剩下\(p_n(x)\)原本的第n项系数,这时候有 $$p_n^{(n)}(c)=f_n^{(n)}(c)=za_n$$
- 这就可以得出 $$a_n=\frac{f_n^{(n)}(c)}{z}$$
- 那么问题就来到了z等于多少上,已知到这一步时,\(P_n(x)\)已经被求导了n次,也就是说这一项的幂减去了n次1,而系数乘上了\(n(n-1)(n-2)(n-3)\ldots 1=n!\),总结得出 $$a_n=\frac{f_n^{(n)}(c)}{n!}$$
- 将其带入Polynomial有 $$P_n(x) = f(c) + f’(c)(x - c) + \frac{f’’(c)}{2!}(x - c)^2 + \cdots + \frac{f^{(n)}(c)}{n!}(x - c)^n$$
Maclaurin Polynomial #
- 麦克劳林级数是Taylor Series的特殊情况,其发生在\(c=0\)的时候,有 $$P_n(x) = f(0) + f’(0)x + \frac{f’’(0)}{2!}x^2 + \frac{f’’’(0)}{3!}x^3 + \cdots + \frac{f^{(n)}(0)}{n!}x^n$$
ex. Finding a 3 degrees Taylor Polynomial for sin x at pi/6 #
以\(\pi/6\)为中心找到sinx的泰勒多项式
- 找Taylor Polynomial实际上只用求原函数在各阶导数下的值就行
- \(f(x) = \sin x \quad f\left(\frac{\pi}{6}\right) = \sin\left(\frac{\pi}{6}\right) = \frac{1}{2}\)
- \(f’(x) = \cos x \quad f’\left(\frac{\pi}{6}\right) = \cos\left(\frac{\pi}{6}\right) = \frac{\sqrt{3}}{2}\)
- \(f’’(x) = -\sin x \quad f’’\left(\frac{\pi}{6}\right) = -\sin\left(\frac{\pi}{6}\right) = -\frac{1}{2}\)
- \(f’’’(x) = -\cos x \quad f’’’\left(\frac{\pi}{6}\right) = -\cos\left(\frac{\pi}{6}\right) = -\frac{\sqrt{3}}{2}\) $$P_3(x) = f\left(\frac{\pi}{6}\right) + f’\left(\frac{\pi}{6}\right) (x - \frac{\pi}{6}) + \frac{f’’\left(\frac{\pi}{6}\right)}{2!} (x - \frac{\pi}{6})^2 + \frac{f’’’\left(\frac{\pi}{6}\right)}{3!} (x - \frac{\pi}{6})^3 $$ $$= \frac{1}{2} + \frac{\sqrt{3}}{2} \left(x - \frac{\pi}{6}\right) - \frac{1}{2(2!)} \left(x - \frac{\pi}{6}\right)^2 - \frac{\sqrt{3}}{2(3!)} \left(x - \frac{\pi}{6}\right)^3$$
Remainder of a Taylor Polynomial #
- 作为一个逼近,其总是存在Error,而Error与实际值之间的差值就是Remainder,有 $$\text{Error} = |R_n(x)| = |f(x) - P_n(x)|$$
Taylor’s Theorem #
- 如果一个函数n+1阶可导在一个包含了c的区间I中,则每一个I中的x都有一个\(z\in [x,c]\)使得 $$f(x) = f(c) + f’(c)(x - c) + \frac{f’’(c)}{2!}(x - c)^2 + \cdots + \frac{f^{(n)}(c)}{n!}(x - c)^n + R_n(x)$$
- 其中 $$R_n(x) = \frac{f^{(n+1)}(z)}{(n+1)!} (x - c)^{n+1}$$
- 以上就是Taylor’s Theorem的完整定理,其可以被总结为一个更加易懂的二级结论,有 $$|R_n(x)| \leq \frac{|x - c|^{n+1}}{(n+1)!} \max |f^{(n+1)}(z)|$$
- 简单来说,直接找到Taylor’s Theroem中的z是十分困难的,这使得其更多像是一个存在性定理,所以实际上这个定理想表达的是这个z的存在使得Remainder能别限制在一个区间
ex. Determing Accuracy of Approximation #
有Thrid Degree Maclaurin Polynomial \(P_3(x) = x - \frac{x^3}{3!}\),求近似\(x=0.1\)时的误差 $$\sin x = x - \frac{x^3}{3!} + R_3(x) = x - \frac{x^3}{3!} + \frac{f^{(4)}(z)}{4!}x^4$$
- 在\(0<z<0.1\)的区间中,\(\sin(0.1)\)有着最大的值,于是有 $$0 < R_3(0.1) = \frac{\sin z}{4!} (0.1)^4 < \frac{0.0001}{4!} \approx 0.000004 $$
ex. Approximating a Value to a Desired Accuracy #
Determine the degree of the Taylor polynomial expanded about c=1 that should be used to approximate \(\ln(1.2)\) so that the error is less than 0.001
- 既然求的是Error Value,直接用Remainder $$|R_n(1.2)| = \left| \frac{f^{(n+1)}(z)}{(n+1)!} (1.2 - 1)^{n+1} \right| = \frac{n!}{z^{n+1}(n + 1)!} (0.2)^{n+1} = \frac{(0.2)^{n+1}}{z^{n+1}(n + 1)}$$
- 要让这玩意小于0.001,由于在\(1<z<1.2\)的区间中 $$\frac{(0.2)^{n+1}}{z^{n+1}(n + 1)}<\frac{(0.2)^{n+1}}{n + 1}<0.001$$
- 最终可以得到 \(n=3\)
Power Series #
- Power Series 幂级数是一种形式为无穷多项式的Series,通常用来近似函数,其表示为 $$\sum_{n=0}^{\infty} c_n (x-a)^n$$
- 其中,\(c_n\)是系数,x是变量,a是幂级数展开的中心点
Center of Power Sereis #
- 中心点的选择是为了确定一个近似最精确的点,如果想要用Power Series来近似\(e^x\),并且对于\(x=1\)这一点的函数更加关心时,就可以选择\(a=1\)为展开的中心点,这使得x=1周围的对于函数的逼近更加精确
Radius and Interval of Convergency #
- 对于一个Power Series来说,只存在三种收敛的情况
-
- Converges at center 只在中心收敛
-
- Converges within a radius R 收敛于一定半径R之间
-
- Converges absolutely for all x 收敛于任意\(x\in R\)
- 通过计算Power Series的Ratio或者Radius Test后便可以知道Radius of Convergency
ex. Finding the radius of Convergence (R=1) #
- 对于Series \(\sum_{n=0}^{\infty} 3(x-2)^n\),找到他的Radius of Convergence
- 利用Ratio Test得到 $$\lim_{n \to \infty} \frac{u_{n+1}}{u_n} = \lim_{n \to \infty} \frac{3(x-2)^{n+1}}{3(x-2)^n} = \lim_{n \to \infty} |x-2| = |x-2|$$
- 已知当这一个极限\(\lim_{n \to \infty} \left| \frac{a_{n+1}}{a_n} \right| < 1\)的时候Series Converge,则有 $$|x-2|<1\Rightarrow -1<x-2<1\Rightarrow 1<x<3\Rightarrow R=1$$
ex. Finding the radius of Convergence (\(R=\infty\)) #
- 判断Series \(\sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{(2n+1)!}\) $$\lim_{n \to \infty} \frac{u_{n+1}}{u_n} = \lim_{n \to \infty} \frac{(-1)^{n+1} x^{2n+3}}{(2n + 3)!} \div \frac{(-1)^n x^{2n+1}}{(2n + 1)!} = \lim_{n \to \infty} \frac{x^2}{(2n + 3)(2n + 2)}=0$$
- 这个情况下,无论x取什么值都有\(\lim_{n \to \infty} \left| \frac{a_{n+1}}{a_n} \right| < 1\),所以R也为\(\infty\)
End Point Convergence #
- 在判断了Convergency Radius后,还需要判断两个End Point的取值情况,这是因为在End Point位于\(\lim_{n \to \infty} \left| \frac{a_{n+1}}{a_n} \right| = 1\)的点,前面提到了这个点处Ratio Test是失效的,所以需要单独计算
ex. Finding Interval of Convergence #
- 判断Series \(\sum_{n=1}^{\infty} \frac{x^n}{n}\)的Interval of Convergence (注意问题变了) $$\lim_{n \to \infty} \frac{u_{n+1}}{u_n} = \lim_{n \to \infty} \frac{x^{n+1} / (n+1)}{x^n / n} = \lim_{n \to \infty} \frac{nx}{n+1} = |x|$$
- 知道了Convergence Radius\(R=1\)后分析两个End Point的Behavior
$$when
x=1:\sum_{n=1}^{\infty} \frac{1}{n} = \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \cdots$$ $$whenx=-1:\sum_{n=1}^{\infty} \frac{(-1)^n}{n} = -1 + \frac{1}{2} - \frac{1}{3} + \frac{1}{4} - \cdots$$ - 最终得到完整Interval of Convergence为 \([-1,1)\)
Properties of Functions Defined by Power Series #
- 如果用一个Power Series来拟合一个function,有 $$f(x) = \sum_{n=0}^{\infty} a_n (x - c)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + a_3 (x - c)^3 + \cdots$$
- 这个function的Derivative的Integral同样也可以用一个Taylor Polynomial表示 $$f’(x) = \sum_{n=1}^{\infty} n a_n (x - c)^{n-1} = a_1 + 2a_2(x - c) + 3a_3(x - c)^2 + \cdots$$ $$\int f(x) , dx = C + \sum_{n=0}^{\infty} a_n \frac{(x - c)^{n+1}}{n+1} = C + a_0 (x - c) + \frac{a_1 (x - c)^2}{2} + \frac{a_2 (x - c)^3}{3} + \cdots$$
- 其Integral和Derivative会有和原函数相同的Radius of convergency,但是由于Series本身发生了改变,导致End Point Behavior可能不同 $$$$
Representation of Functions by Power Series #
- 考虑一个function \(f(x) = \frac{1}{1 - x}\)
- 这个function长得非常像在前面所提到的Geometric Series的Partial Sum,具体来说一个Geometric Series会在\(0<|r|<1\)的时候有 $$\sum_{n=0}^{\infty} ar^n = \frac{a}{1 - r}$$
- 而对于上面的\(f(x)\),当 \(a=1,r=x\) 的时候就有 $$\frac{1}{1 - x} = \sum_{n=0}^{\infty} ar^n = \sum_{n=0}^{\infty} x^n = 1 + x + x^2 + x^3 + \cdots, \quad |x| < 1. $$
- 当然要知道一个Power Series存在Convergence Radius,这使得这个Series仅在\((-1,1)\)的区间上拟合了function,如果需要研究函数在其他区间的拟合,则可以更改Power Series的c
- 比如当 \(c=-1\) 的时候就有 $$\frac{1}{1 - x} = \frac{1}{2 - (x + 1)} = \frac{\frac{1}{2}}{1 -\frac{(x + 1)}{2}} = \frac{a}{1 - r}$$
- 于是可以得出 \(a= \frac{1}{2},r=\frac{x+1}{2}\),带入Power Series中有 $$\frac{1}{1 - x} = \sum_{n=0}^{\infty} \left(\frac{1}{2}\right)\left(\frac{x+1}{2}\right)^n = \frac{1}{2} \left[ 1 + \frac{x+1}{2} + \left(\frac{x+1}{2}\right)^2 + \left(\frac{x+1}{2}\right)^3 + \cdots \right], \quad |x+1| < 2$$
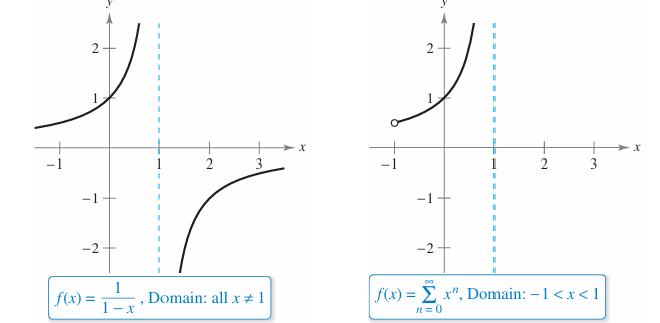
Power Series仅在Convergence Interval中拟合Function
ex. Find Geometeric Power Sereis Centerd at 0 #
找一个拟合function \(f(x) = \frac{4}{x + 2}\) 的Power Series
- 将function写成 \(\frac{a}{1-r}\) 的形式 $$\frac{4}{2 + x} = \frac{2}{1 - \left(-\frac{x}{2}\right)} = \frac{a}{1 - r}$$
- 有 \(a=2,r=\frac{-x}{2}\)
- 于是可以写出Power Series $$\frac{4}{x + 2} = \sum_{n=0}^{\infty} a r^n = \sum_{n=0}^{\infty} 2 \left(-\frac{x}{2}\right)^n = 2 \left(1 - \frac{x}{2} + \frac{x^2}{4} - \frac{x^3}{8} + \cdots \right)$$
Operations with Power Series #
$$f(x) = \sum_{n=0}^{\infty} a_n x^n \text{ and } g(x) = \sum_{n=0}^{\infty} b_n x^n$$ $$f(kx) =\sum_{n=0}^{\infty} a_n (kx)^n$$ $$f(x^N) =\sum_{n=0}^{\infty} a_n (x^N)^n$$ $$f(x) \pm g(x) = \sum_{n=0}^{\infty} (a_n + b_n) x^n$$
ex. Finding Power Series by Integration #
- 前面提到了Power Series的Integral和Derivative也都还是Power Series,于是当一个函数的积分或者导数可以被整理为一个Geometric Power Series时,该函数也可以用Power Series来表示
找到Power Series Representation of \(f(x)=\ln x\)
- 已知\(\int f(x)dx=\frac1x+C\),有 $$\frac{1}{x} = \sum_{n=0}^{\infty} (-1)^n (x - 1)^n$$
- 这是一个 \(a=1,r=-(x-1)\) 的Power Series,对这个Power Series积分有 $$\ln x = \int \frac{1}{x} , dx + C = C + \sum_{n=0}^{\infty} (-1)^n \frac{(x - 1)^{n+1}}{n+1}= \frac{(x-1)}{1} - \frac{(x-1)^2}{2} + \frac{(x-1)^3}{3} - \frac{(x-1)^4}{4} + \cdots $$
ex. 2. Finding a Power Series by Integration #
找到 \(g(x)=\arctan x\) 的Power Series
- 已知\(\arctan(x)\)的Derivative为\(\frac{1}{1+x^2}\),令\(x^2\)为r,就可以写出他的Power Series有 $$f(x^2) = \frac{1}{1 + x^2} = \sum_{n=0}^{\infty} (-1)^n x^{2n}$$
- 再对这玩意积分,有 $$\arctan x = \int \frac{1}{1 + x^2} , dx + C = C + \sum_{n=0}^{\infty} (-1)^n \frac{x^{2n+1}}{2n+1}$$
- 令 \(x=1\) 可以知道 \(C=0\),有 $$= \sum_{n=0}^{\infty} (-1)^n \frac{x^{2n+1}}{2n+1} = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots$$
Taylor and Maclaurin Series #
- 在前面通过了使用Geometric Series的Partial Sum找到了很多函数对于的Power Series,通过Taylor Series则可以找到那些可以被求导n次的函数的Power Series
- 前面提到了Taylor Polynomial拟合的function在他的Radius of Convergence中可以表示为 $$f(x) = f(c) + f’(c)(x - c) + \frac{f’’(c)}{2!}(x - c)^2 + \cdots + \frac{f^{(n)}(c)}{n!}(x - c)^n + \cdots$$
- 这个Polynomial也是不同Power的和,当\(n=\infty\)的时候,其也可以被当作一个Series,有 $$\sum_{n=0}^{\infty} \frac{f^{(n)}(c)}{n!} (x - c)^n = f(c) + f’(c)(x - c) + \cdots + \frac{f^{(n)}(c)}{n!}(x - c)^n + \cdots $$
- 这时候只要Taylor Series Converge,其就完全的拟合了Function
Binomial Series #
- 对于形如 \(f(x)=(1+x)^k\) 的function,可以通过Binomial Serises逼近,因为其本身就是一个Binomial 二项式,当然可以同Series来表示他的二项式展开,经典二项式定理为 $$(1+x)^k = \sum_{n=0}^k \binom{k}{n} x^n$$
- 但经典二项式定理存在一个前提为 \(k\in \mathbb z^+\),当k不为整数的时候,二项式系数不会在某一项后归零,导致级数没有终止,这就导致了二项式展开变成了Seires,有 $$(1 + x)^k = 1 + kx + \frac{k(k-1)x^2}{2!} + \frac{k(k-1)(k-2)x^3}{3!} + \frac{k(k-1)(k-2)(k-3)x^4}{4!} + \cdots$$
POWER SERIES FOR ELEMENTARY FUNCTIONS #
$$\frac{1}{x} = 1 - (x - 1) + (x - 1)^2 - (x - 1)^3 + \cdots, \quad 0 < x < 2$$ $$\frac{1}{1 + x} = 1 - x + x^2 - x^3 + x^4 - \cdots, \quad -1 < x < 1$$ $$\ln x = (x - 1) - \frac{(x - 1)^2}{2} + \frac{(x - 1)^3}{3} - \frac{(x - 1)^4}{4} + \cdots, \quad 0 < x < 2$$ $$e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \cdots, \quad -\infty < x < \infty$$ $$\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots, \quad -\infty < x < \infty$$ $$\cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots, \quad -\infty < x < \infty$$ $$\arctan x = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots, \quad -1 \leq x \leq 1$$ $$\arctan x = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots, \quad -1 \leq x \leq 1$$ $$\arcsin x = x + \frac{1 \cdot 3 x^3}{2 \cdot 4} + \frac{1 \cdot 3 \cdot 5 x^5}{2 \cdot 4 \cdot 6} + \cdots, \quad -1 \leq x \leq 1$$ $$(1 + x)^k = 1 + kx + \frac{k(k-1)x^2}{2!} + \frac{k(k-1)(k-2)x^3}{3!} + \cdots, \quad -1 < x < 1^*$$