Last Edit: 1/9/25
1. Imaginary and complex numbers #
- Real Number 实数,包含了Reation & Irrational Number一直以来拥有一个Fundamental Property就是 Square of any real number is always nonnegative
- 换句话来说,方程\(x^2=-1\)在实数域是无解的,但这并不代表这个方程无解
- 要分析这一问题,首先就需要定义\(\sqrt{-1}\)
Definition of Imaginary Number #
- An imaginary number is a number of the form bi, where b is real and $$i=\sqrt{-1}$$
- 定义指出Complex Number是形式为\(bi\)的数,其中b为Real Number
- 有了这定义,我们便可以为任意Real Number找到对应的Square Root,具体来说 $$(bi)^2=b^2\cdot i^2=b^2\cdot -1=-b^2$$
- 例如\((3i)^2=-9,\sqrt{-9}=3i\)
ex. #
Solve the equation \(x^2 +2x+2 = 0\). Using the quadratic formula $$z_1 = \frac{-2 + \sqrt{4 - 8}}{2} = -1 + i \quad \text{and} \quad z_2 = \frac{-2 - \sqrt{4 - 8}}{2} = -1 - i. $$
Definition of Complex Number #
- A complex number is a number of the form \(z = a+bi\), where a and b are real numbers
- 其中a和b分别被称为z的Real & Imaginary Parts
$$a=Re(z)
和b=Im(z)$$ - If \(Re(z) = 0\), then z is an imaginary number and if \(Im(z) = 0\), then z is a real number
- 可以发现对于上面的例子\(z_1\)和\(z_2\),\(Re(z_1)=Re(z_2),Im(z_1)=-Im(z_2)\),这并不是一个巧合,而是可以引出另一个Complex Number的特性,Complex Conjugate
Definition of Complex Conjugate #
- The complex conjugate of \(a+bi\) is the number \(a-bi\). We use a bar over the number to denote the conjugate $$\overline{a + bi} = a - bi$$
- 对于二次方程\(x^2 + \beta x + \gamma = 0\) 中的\(\beta^2 - 4\alpha\gamma < 0\) 时,该方程没有实数解,但可以有复数解。这种情况下,解是共轭复数对。解可以通过标准的二次公式来计算: $$a = \frac{-\beta}{2\alpha},b = \frac{\sqrt{|\beta^2 - 4\alpha\gamma|}}{2\alpha}$$
- 其中\(a + bi\) 和 \(a - bi\) 分别是这个二次方程的两个解。
- z = a 是一个实数,则它的复数共轭是它自身,即\(\overline{z} = z\),这表明实数是它们自己的共轭。此外,任何复数z的共轭的共轭是z本身,即\(\overline{\overline{z}} = z\)
2. Complex Arithmetic 复数运算 #
- Complex numbers和Real Number一样也可以坐加减乘除运算,并且commutativity, associativity and distributivity等特性依然存在
Addition and Sibtraction #
- 要给两个Complex Numbers做加减,分别加减他们的Real and Imaginary Components $$(a+bi)+(c+di)=(a+b)+(b+d)i$$
Propisition 2.1 Complex Number’s Conjugate #
对于任何复数z,
- \(z + \overline{z} = 2 \cdot \text{Re}(z)\)
- \(z - \overline{z} = 2 \cdot \text{Im}(z) \cdot i\)
Proof #
假设\(z = a + bi\),其中a是实部,b是虚部,那么:
- \(z + \overline{z} = (a + bi) + (a - bi) = 2a = 2 \text{Re}(z)\)。这说明复数和其共轭的和是两倍实部
- \(z - \overline{z} = (a + bi) - (a - bi) = 2bi = 2 \text{Im}(z) \cdot i\)。这说明复数和其共轭的差是两倍虚部的虚数单位
2.2 Multiplication #
$$(a +bi) (c+di) = ac+adi +cbi +bdi^2 = (ac-bd)+(ad+bc)i$$
2.3 Division #
- Complex Number的除法可以视为乘以其逆元。复数\(z = a + bi\)的逆元\(z^{-1}\)满足\(z \cdot z^{-1} = 1\)。
- 给定非零复数\(a + bi\),求解使得\((a + bi)(x + yi) = 1\)的复数\(x + yi\),整理后得到:
- \(ax - by = 1\)
- \(bx + ay = 0\)
- 这两个方程可以通过以下步骤解决:
- 将方程 (2) 乘以a,方程 (3) 乘以b,然后将两个结果相加,消去y得到\((a^2 + b^2)x = a\),从而解得\(x = \frac{a}{a^2 + b^2}\)
- 类似地,将方程 (2) 乘以−b,方程 (3) 乘以a,然后将两个结果相加,消去x得到\((a^2 + b^2)y = -b\),从而解得\(y = \frac{-b}{a^2 + b^2}\)
- 这样,复数\(a + bi\)的乘法逆元\(x + yi\)可以表示为: $$x = \frac{a}{a^2 + b^2},y = \frac{-b}{a^2 + b^2}$$
Proposition 2.2 Complex Number’s Division #
- 所以当Complex Number \(a+bi\neq 0\),then $$(a + bi)^{-1} = \frac{a}{a^2 + b^2} - \frac{b}{a^2 + b^2}i$$
- 这样就可以做除法的运算了,便有 $$\frac{c + di}{a + bi} = (c + di) \cdot (a + bi)^{-1} = (c + di) \cdot \left(\frac{a}{a^2 + b^2} - \frac{b}{a^2 + b^2}i\right) = \frac{ac + bd}{a^2 + b^2} + \frac{ad - bc}{a^2 + b^2}i$$
Proposition 2.3 Complex Number’s Conjugate’s Property #
- 对于Complex Numbers z 和 w, $$\overline{z+w}=\overline{z}+\overline{w},\overline{z\cdot w}=\overline{z}\cdot \overline{w},if~w\neq ~\overline{(\frac{z}{w})}=\frac{\overline{z}}{\overline{w}}$$
Proof #
$$\begin{aligned} \overline{(a + bi) + (c + di)} &= \overline{(a + c) + (b + d)i} \ &= (a + c) - (b + d)i \ &= (a - bi) + (c - di) \ &= \overline{(a + bi)} + \overline{(c + di)} \end{aligned}$$ $$\begin{aligned} \overline{(a + bi),(c + di)} &= \overline{(ac - bd) + (ad + bc),i} \ &= (ac - bd) - (ad + bc),i \ &= (a - bi),(c - di) \ &= \overline{(a + bi)} ,\cdot, \overline{(c + di)} \end{aligned}$$
3. The Geometry of Complex Numbers #
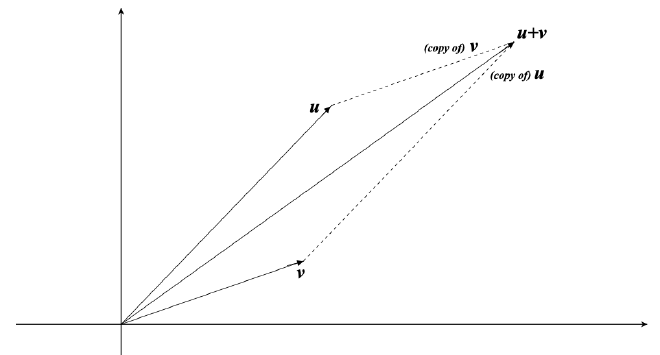
- 对于Complex Number来说,其可以通过Complex Plane来表示,其中两个轴分别是Real Axis和Imaginary Axis
- 每一个复数可以被视为起始于原点的向量,而复数的加法可以通过向量加法在几何上表示出来
3.2 The modulus of a Complex Number #
- 对于Real Number来说,其Magnitude可以通过Absolute Value\(|a|\)来得到,这同理也可以运用到Complex Number上
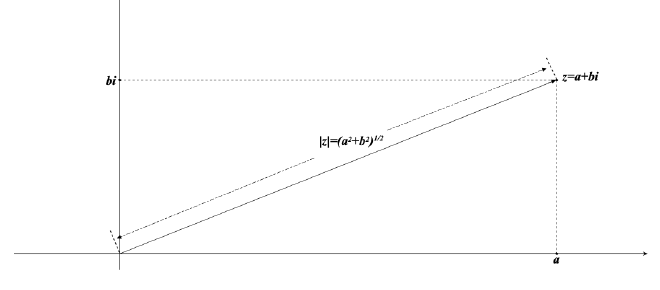
Definition of modulus of Complex Number #
- The modulus, or absolute value, of a complex number \(z= a+ bi\), is denoted by \(|z|\) and defined to be the distance in the complex plane between the point z and the point 0
Proposition 3.1 Complex Number’s Conjugate & Modulus #
- For any Complex Number z $$|z|^2=z\cdot \overline z$$
Proof #
- 假设有Complex Number z,根据Complex Number的Modulus可以得到\(|z|^2=a^2+b^2\) $$z\cdot \overline z=(a+bi)(a-bi)=a^2-abi+abi-b^2i^2=a^2+b^2=|z|^2$$
- 于是当\(z\neq 0\)的情况下, $$z^{-1}=\frac{\overline z}{|z|^2}$$
- 这与上面Proposition 2.2 Complex Number’s Division的内容相似
Proposition 3.2 Commutative Property #
- \(|z\cdot w|=|z|\cdot |w|\) $$|z \cdot w|^2 = (z \cdot w) \cdot (\overline{z \cdot w}) = z \cdot w \cdot \overline{z} \cdot \overline{w} = |z|^2 \cdot |w|^2$$
- 两边同时取Square Root可以得到 $$|z \cdot w| = \sqrt{|z \cdot w|^2} = \sqrt{|z|^2 \cdot |w|^2} = \sqrt{|z|} \cdot \sqrt{|w|} = |z| \cdot |w| $$
Proposition 3.3 Inverse #
- If \(z\neq 0,then~|z^{-1}|=(|z|)^{-1}\)
3.3 The Argument of a Complex Number 复数的辐角 #
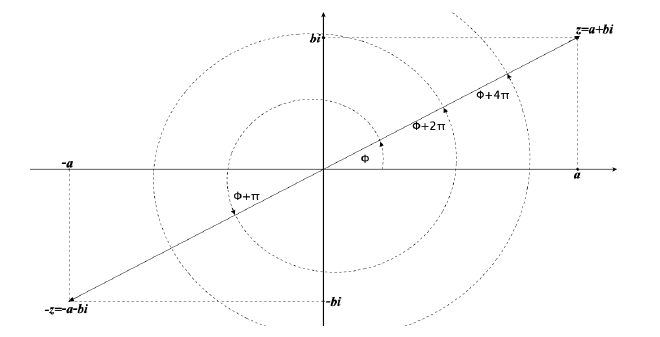
- 如果说Modulus决定了一个Complex Number的Magnitude,他的Angle则是被Argument决定
- The argument (or phase) of \(z= a+ bi(z\neq 0)\)is ‘the’ angle, \(φ\) between the positive real axis and the line segment connecting z to 0
- The argument of z is denoted by arg(z)
- 通常情况下,复数的辐角是多值的,因为角度可以通过加上\(2\pi\)的整数倍来得到相同的方向
- 求的Complex Number的Argument的办法就是通过\(\arctan\)函数
- 在不同Quadrant下的Complex Number所得到的Argument则需要有所调整,具体来说
- 第一象限\(a > 0, b > 0\),直接使用\(\arctan(b/a)\),无需调整。
- 第二象限\(a<0,b>0\),\(arctan(b/a)\) 计算的是一个负值,但实际的Argument应是\(\pi\)加上这个负值。所以,辐角是\(\pi + \text{arctan}(b/a)\)
- 第三象限\(a<0,b<0\),此时\(\text{arctan}(b/a)\)产生正值,但由于在第三象限,所需的辐角是这个值减去\(\pi\),即\(\arctan(b/a) - \pi\)
- 第四象限\(a>0,b<0\),在此象限,\(\arctan(b/a)\) 本身就是正确的辐角值,因为它会给出负的角度值。
- 特殊情况a = 0 时,辐角取决于b的符号:
- 如果\(b>0\),辐角是\(\frac{\pi}{2}\), 如果\(b<0\),辐角是\(\frac{3\pi}{2}\)
3.4 The polar-coordinate representation of complex numbers. #
- 在分别求得了Complex Number的Modulus和Argument后,便可以求出Complex Number的Polar Coordinate
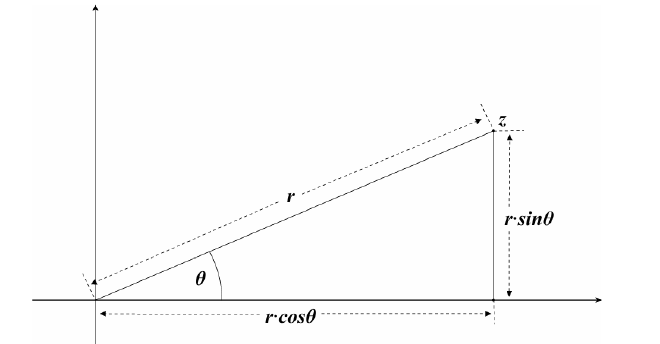
- 其于正常的Polar Coordinate一样,\(Re(z)=r\cos\theta,Im(z)=r\sin \theta,z=r(\cos \theta+i\sin \theta)\)
Proposition 3.5 Argument’s Associative Law #
- \(arg(z_1z_2)=arg(z_1)+arg(z_2)\)
- 有\(z_1 = r \bigl(\cos \theta + i \sin \theta\bigr), \quad z_2 = \rho \bigl(\cos \phi + i \sin \phi\bigr)\) $$z_1 z_2 = \bigl(r(\cos \theta + i \sin \theta)\bigr) \cdot \bigl(\rho(\cos \phi + i \sin \phi)\bigr) =r\rho ,\Bigl((\cos \theta + i \sin \theta),(\cos \phi + i \sin \phi)\Bigr)$$
- 其中\((\cos \theta + i \sin \theta),(\cos \phi + i \sin \phi)= (\cos \theta)(\cos \phi) + (\cos \theta)(i \sin \phi) + (i \sin \theta)(\cos \phi) + (i \sin \theta)(i \sin \phi)\)
- 当把各项一一对应起来后,就会发现 $$\cos(\theta + \phi) + i,\sin(\theta + \phi)$$
- 所以 $$z_1 z_2 = r\rho ,\bigl(\cos(\theta + \phi) + i \sin(\theta + \phi)\bigr)$$
- 由此得出\(\arg(z_1 z_2) = \arg(z_1) + \arg(z_2)\)
- 同理Argument的取值范围应为\((-\pi,\pi]\),所以
- 当\(\text{arg}(z_1) + \text{arg}(z_2) > \pi\), 为了将结果拉回到\((-\pi, \pi]\)的范围内,需要从这个和中减去\(2\pi\)
- 当\(\text{arg}(z_1) + \text{arg}(z_2) < -\pi\) 为了将结果拉回到\((-\pi, \pi]\)的范围内,需要在这个和中加上\(2\pi\)
Proposition 3.6 #
- 如果\(z \neq 0\),且w是任意复数,那么将w乘以z:
- 会将w的模(大小)按\(|z|\)进行伸缩(即缩小或放大)
- 会将w的辐角(方向角)按\(\text{arg}(z)\)旋转
- 这说明复数乘法对复数的几何意义是模的缩放和角度的旋转
3.5 Exponential Notation Euler’s formula 欧拉公式 #
- 对于实数\(\theta\),复数可以表示为:\(\cos\theta + i\sin\theta = e^{i\theta}\)
- 这表明复数的极坐标表示(幅角和模)可以用指数形式表示
Proof #
- 对于Euler’s Formula的推导从Taylor expansion开始
- 已知指数函数 exe^x 在实数域中的泰勒展开式为: $$e^x = \sum_{n=0}^\infty \frac{x^n}{n!} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots$$
- 将\(x\)替换为\(i\theta\)可以得到 $$e^{i\theta} = \sum_{n=0}^\infty \frac{(i\theta)^n}{n!}$$
- 已知Imaginary Number i在Even次Exponent下均为\(-1\),可以得到 $$e^{i\theta} = \sum_{n=0}^\infty \frac{(i\theta)^n}{n!} = \sum_{n=0}^\infty \frac{(-1)^n\theta^{2n}}{(2n)!} + i \sum_{n=0}^\infty \frac{(-1)^n\theta^{2n+1}}{(2n+1)!}$$
- 这两个Series分别对应余弦和正弦的泰勒展开式,于是便有 $$e^{i\theta} = \cos\theta + i\sin\theta$$
Proposition 3.7 #
- If \(z= r > 0\) and \(\theta= arg(z)\), then $$z=r\cdot e^{\theta i}$$
- 本质上就是\(z=r(\cos\theta +i\sin\theta)\),因为有Eulers’ Formula
Proposition 3.8 #
- For any number and any integer k $$e^{(\theta+2k\pi)i}=e^{\theta i}$$
Proof #
- 从Euler’s Formula入手,已知\(e^{(\theta+2k\pi )i}=e^{\theta i}\cdot e^{2k\pi i}\)
- 令\(2k\pi = \theta\),有 $$e^{(\theta+2k\pi )i}=e^{\theta}\cdot(\cos 2\pi+i\sin 2\pi)=e^{\theta}$$
4. Roots of polynomials #
4.1 The fundamental theorem of algebra #
- 如果P(z)是一个次数为n > 0的多项式,其形式为: $$P(z) = c_n z^n + c_{n-1} z^{n-1} + \cdots + c_1 z + c_0$$
- 其中\(c_n\)为Complex Numbers
- 那么,The fundamental theorem of algebra 表明 \(P(z) = 0\) has a Solution in the Complex
- 一个例子便是对于实数系数多项式\(P(x) = x^2 + 1\),其has no real solutions,但在Complex Number中有两个解\(i和-i\)
Propisition 4.1 #
- 对于任意次数\(n \geq 1\)的复系数多项式\(P(z)\),可以表示为: $$P(z) = c_n \cdot (z - \zeta_1)(z - \zeta_2) \cdots (z - \zeta_n)$$
- 与Real Number roots一样,并不是所有的根\(\zeta_1, \dots, \zeta_n\)都是不同的,某些根可能会重复,称为Reapeated Root
- 一个例子便是\(Q(z) = z^4 - 2z^3 + 2z^2 - 2z + 1\),其因式分解为: $$Q(z) = (z - 1)(z - 1)(z - i)(z + i)$$
Proposition 4.2 #
如果 P(z)P(z) 是一个次数\(n \geq 1\)且具有复系数的多项式,那么:
- P(z) 至少有一个根(The fundamental theorem of algebra)
- P(z) 最多有n个根(Included Repeated Roots)
4.2 Polynomials with real coefficients #
- 4.1介绍了Coefficients为Complex Numbers的情况,由于Real Number是Complex Number的Subset,所以当Coeffcients为Real Number的时候,其也有Root
- 但即使是Real Number的Coefficient,其也不保证Root为Real Number
Proposition 4.3 #
- 如果\(P(z) = a_n z^n + a_{n-1} z^{n-1} + \cdots + a_1 z + a_0\)是一个Real Number Coefficients Polynomial,并且\(\zeta\)是P(z)的一个根,那么其Complex Conjugate\(\overline{\zeta}\)也是P(z)的一个根
Proof #
- 假设\(\zeta\)是P(z)的一个根,即: $$a_n \zeta^n + a_{n-1} \zeta^{n-1} + \cdots + a_1 \zeta + a_0 = 0$$
- 对等式两边取共轭: $$\overline{a_n \zeta^n + a_{n-1} \zeta^{n-1} + \cdots + a_1 \zeta + a_0} = 0$$
- 利用共轭的性质 $$\overline{a_k \zeta^k} = \overline{a_k} \cdot \overline{\zeta^k} = a_k \cdot (\overline{\zeta})^k$$
- 因为\(a_k\)是实数,因此等式变为 $$a_n (\overline{\zeta})^n + a_{n-1} (\overline{\zeta})^{n-1} + \cdots + a_1 \overline{\zeta} + a_0 = 0$$
- 这说明\(\overline{\zeta}\)也是P(z)的一个根
Proposition 4.4 #
- 如果多项式的系数是Real Number,那么其Complex Root必然成共轭对出现
Proposition 4.5 #
- 对于一个Real Number Coefficient Polynomial: $$P(z) = a_n z^n + a_{n-1} z^{n-1} + \cdots + a_1 z + a_0$$
- 其可以表示为以下因式分解形式: $$P(z) = a_n (z - \xi_1)(z - \xi_2)\cdots(z - \xi_m) Q_1(z) Q_2(z) \cdots Q_k(z)$$
- 其中\(\xi_1, \dots, \xi_m\):是所有的Real Roots
- \(Q_j(z) = z^2 - 2\text{Re}(\zeta_j)z + |\zeta_j|^2\):是与复数根和其共轭对应的实系数二次多项式
4.3 Square roots and quadratic equations #
- 想要求解General Quadratic Equation,需要先算出Complex Number的Square Roots
Propposition 4.6 #
- 如果\(u \neq 0\),那么复数方程\(z^2 = u\)的解是: $$\zeta_1 = \sqrt{|u|} e^{i\theta/2}, \quad \zeta_2 = -\zeta_1$$
Proof #
- 已知任何非零复数u都可以表示为\(u = |u| e^{i\theta}\)
- 于是可以得出其中的一个Root为\(\zeta_1 = \sqrt{|u|} e^{i\theta/2}\)
- 另一个解则是\(\zeta_2 = -\zeta_1\)
Proposition 4.7 #
- 对于二次方程: $$az^2 + bz + c = 0$$ 其解的公式为: $$z_1 = \frac{-b + \sqrt{b^2 - 4ac}}{2a}, \quad z_2 = \frac{-b - \sqrt{b^2 - 4ac}}{2a}$$
- 其中:a, b, c 是复数(且\(a \neq 0\)),公式中的平方根\(\sqrt{b^2 - 4ac}\) 按复数的平方根规则计算。
Example 4.3 #
$$z^2 + (1 - 2i)z - 2i = 0$$
- 这里\(a = 1,b = 1 - 2i,c = -2i\) $$\zeta_1 = \frac{-(1 - 2i) + \sqrt{(1 - 2i)^2 - 4(1)(-2i)}}{2}, \quad \zeta_2 = \frac{-(1 - 2i) - \sqrt{(1 - 2i)^2 - 4(1)(-2i)}}{2}$$ $$b^2 - 4ac = (1 - 2i)^2 - 4(-2i) = 1 - 4i + 4 - 8i = -3 - 4i + 8i = -3 + 4i$$
- 根据公式\(\sqrt{|b^2 - 4ac|} e^{i\theta/2}\)计算其复数平方根\(\sqrt{-3 + 4i} = 1 - 2i\) $$\zeta_1 = \frac{-b + \sqrt{-3 + 4i}}{2} = \frac{-(1 - 2i) + (1 - 2i)}{2} = 2i$$$$\zeta_2 = \frac{-b - \sqrt{-3 + 4i}}{2} = \frac{-(1 - 2i) - (1 - 2i)}{2} = -1$$
4.4 The nth roots of a complex number #
- 对于一个正实数\(\alpha > 0\)和正整数n,\(\alpha\)的n次根\(\beta\)定义为: $$\beta^n = \alpha \quad \text{或} \quad \beta = \alpha^{1/n}$$
- 这是解决方程\(z^n - \alpha = 0\)的一个特定解,通常选择正实数解作为主n次根
- 若\(u \neq 0\)是一个复数,且n是正整数,那么方程\(z^n = u\)总共有n个不同的复数解,这些解可以记为\(\zeta_1, \zeta_2, \dots, \zeta_n\) $$z^n - u = (z - \zeta_1)(z - \zeta_2)\cdots(z - \zeta_n)$$
Proposition 4.8 #
- 对于复数\(u \neq 0\),如果\(\theta = \text{arg}(u)\),n是一个正整数,那么方程\(z^n = u\)的解为: $$\zeta_k = \sqrt[n]{|u|} e^{i\left(\frac{\theta + 2k\pi}{n}\right)}, \quad k = 0, 1, 2, \dots, n-1$$
- 其中总共有n个不同的解,这些解在复平面上均匀分布,构成一个以原点为中心、半径为\(\sqrt[n]{|u|}\)的正n边形。
Proof #
- 对于任意k来说,有 $$\zeta_k = \sqrt[n]{|u|} e^{i\left(\frac{\theta + 2k\pi}{n}\right)}$$
- 计算\(\zeta_k^n\) $$\zeta_k^n = \left(\sqrt[n]{|u|}\right)^n \cdot \left(e^{i\left(\frac{\theta + 2k\pi}{n}\right)}\right)^n$$ $$\left(\sqrt[n]{|u|}\right)^n = |u|,\left(e^{i\left(\frac{\theta + 2k\pi}{n}\right)}\right)^n = e^{i\left(\theta + 2k\pi\right)} = e^{i\theta}$$
- 所以 $$\zeta_k^n = |u| e^{i\theta} = u$$
- 这表明每个\(\zeta_k\)都是\(z^n = u\)的解
- 在这之后还需要验证解是不同的\(\zeta_k \neq \zeta_j\),假设\(\zeta_k = \zeta_j\),那么\(\frac{\zeta_k}{\zeta_j} = 1\) $$\frac{\zeta_k}{\zeta_j} = \frac{\sqrt[n]{|u|} e^{i\left(\frac{\theta + 2k\pi}{n}\right)}}{\sqrt[n]{|u|} e^{i\left(\frac{\theta + $2j\pi}{n}\right)}} = e^{i\left(\frac{2(k-j)\pi}{n}\right)}$$
- 若\(\frac{\zeta_k}{\zeta_j} = 1\),则必须有: $$\frac{2(k-j)\pi}{n} = 2m\pi \quad (m \in \mathbb{Z})$$
- 这意味着: $$\frac{k-j}{n} = m \quad \Rightarrow \quad k-j = mn$$
- 由于\(0 \leq k, j < n\),因此\(|k-j| < n\),所以只有m = 0,即k = j。
- 这表明当\(k \neq j\)时,\(\zeta_k \neq \zeta_j\)